抽象代数

参考教材:密码编码学与网络安全

AES加密的数学基础

第一遍读感觉教材上对数学基础(群环域,多项式运算)P72-P91给的莫名奇妙

然后参考了知乎回答对群环域的解释

此时第二遍读教材,发现其实教材在讲每一部分的开始都写了为什么要讲.

学习这部分一定要明确目的,在陷入定理的证明时或者公式应用时时刻想想是在干什么

引入多项式构造$GF(p^n)$这一想法真的太神奇了,将整数上的数论定理应用于多项式也真的太神奇了

另,教材P74页的图4.2是有错误的

抽象代数基础

图片来自代数结构入门：群、环、域、向量空间 - 知乎 (zhihu.com)

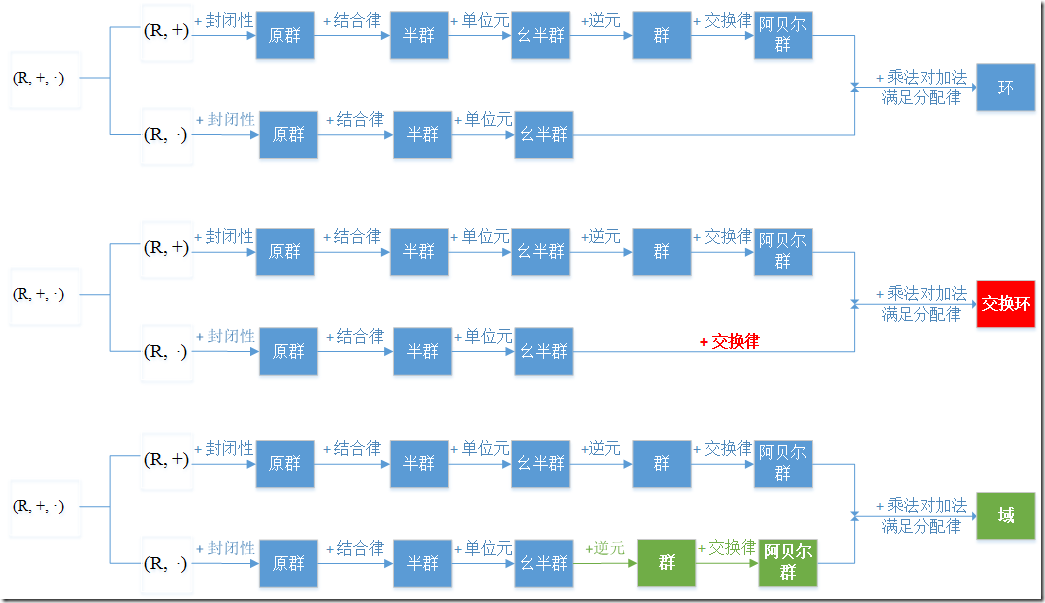
群

$<G,·>$表示一个定义了二元关系$·$的集合(注意这里$·$不一定是乘号,可以是所有二元关系的抽象表示)

如果G满足:

A1封闭性:$\forall a,b\in G\rightarrow a·b\in b$

A2结合律:$\forall a,b\in G,a·(b·c)=(a·b)·c$

A3单位元:$\exist e\in G,\forall a\in G,e·a=a·e=a$

A4逆元:$\forall a\in G,\exist a^{-1},a·a^{-1}=a^{-1}·a=e$

这里$^{-1}$不是一定是-1次幂,只是逆元的表示形式

集合G+A1+A2+A3+A4=群G

<Z,+>就是一个群

<N,+>就不是一个群,因为如果定义单位元是0,那么1的逆元就是-1,但是-1不在自然数范围内,满足A1A2A3但是不满足A4的代数系统被称为幺半群

变换群

设A是一非空集合,G是A到A的映射集合,如果G关于运算*构成一个群,则称$<G,✳>$是集合A上的一个变换群,简称变换群

置换群

设A是一非空有限集合,则A上的一个变换群就是A的一个置换群,简称置换群

交换群

A5交换律:$\forall a,b\in G,a·b=b·a$

群G+A5=交换群G

环

$<R,+,\times>$R是一个有两种二元运算的集合,这两种二元运算分别为加法$+$和乘法$\times$

已知$<R,+>$是交换群

如果R再满足

M1乘法封闭性:$\forall a,b\in R,a\times b\in R$

M2乘法结合律:$\forall a,b,c\in R,a\times (b\times c)=(a\times b)\times c$

M3乘法对加法的分配律:$\forall a,b,c\in R,\begin{cases}a\times (b+c)=a\times b+a\times c\(a+b)\times c=a\times c+b\times c\end{cases}$

注意这里没有写$a \times (b+c)=(b+c)\times a$

因为这样写实际上是满足乘法交换律,而满足分配律不一定满足交换律,比如矩阵乘法

矩阵的左右乘结果一般是不一样的,但是矩阵乘法对矩阵加法是有结合律的

则称R为环

交换环

如果环R再满足

M4乘法交换律:$\forall a,b,c\in R,(a\times b)\times c=a\times (b\times c)$

显然$R_n(Q)$是环但不是交换环

则称R为交换环

整环

如果交换环R再满足

M5乘法单位元:$\exist e,\forall a\in R,e\times a=a\times e=a$

当$R=S$为整数时,$e=1$

当$R=R_n(Q)$,n阶实数矩阵集合,$e=E(n)$n阶单位矩阵

M6无零因子,:$\forall a,b\in R,a\times b=0\rightarrow a=0\ or\ b=0$

则称R为整环

怎么理解”无0因子”?

显然$R_n(Q)$不满足M6,因为两个矩阵$A,B$乘积是个0矩阵并不能说明$A$或者$B$矩阵有至少一个是零矩阵

比如

$$
A=\begin{bmatrix}
0\ 0\ 0\
0\ 0\ 0\
0\ 0\ 1\
\end{bmatrix}\ \ \ \ \
B=\begin{bmatrix}
0\ 0\ 1\
0\ 0\ 0\
0\ 0\ 0\
\end{bmatrix}
$$
又如,

令$Z_6={0,1,2,3,4,5}$,

定义$Z_6$上的乘法$\otimes$为$a\otimes b=(a\times b\ )mod\ 6$

定义$Z_6$上的加法$\oplus$为$a\oplus b=(a+b)mod\ 6$

显然$Z_6$满足$A_1-A_5,M_1-M_5$

但是$<Z_6,+,\times>$不满足无零因子,比如

$2\otimes 3=(2\times 3)mod \ 6=6mod\ 6=0$

就是说,0这个元素一定也是在集合R中存在的,并且乘法运算结果为0一定和引入这个元素0有关

域

设$<R,+,\times>$为一个整环,如果R再满足

M7乘法逆元:$\forall a≠0\in R,\exist a^{-1}\in R,a\times a^{-1}=1$则称$a^{-1}$为a的乘法逆元

注意乘法逆元也是$R$中的

定义乘法逆元的作用实际上是可以使用除法,除以一个数等于乘以该数的乘法逆元

比如对于$<Z_7,+,\times>$,由拓展欧几里得定理可知,由于模数为7是一个质数,因此0到6都存在$Z_7$上的mod 7意义下的乘法逆元

再比如全体整数就不是任何元素都有乘法逆元,只有1和-1有乘法逆元,任何绝对值大于1的整数其乘法逆元应该是分数,不属于整数.

则称R为域F

有限域GF(p)

符号意义:

$GF(p)=<Z_p,\oplus,\otimes >$

$GF:Galois Field$,伽罗华域

$p$:表示一个正素数

$\oplus:\forall a,b\in Z_p,a\oplus b=(a+b)\ mod\ p$即模p加法

$\otimes : \forall a,b\in Z_p,a\otimes b=(a\times b)\ mod\ p$即模屁乘法

为什么一定要求是一个素数?

当N为一个合数的时候$Z_N={1,2,3,…,N-2,N-1}$不满足$M_6$无零因子,不是整环,因此不是域

为什么不满足$M_6$?

由已知,N是合数,则至少存在$n\in Z_N,1<n<N,n|N$

如果$n^2=N$,则有$n\otimes n=n\times n\ mod\ N=0$

如果$n^2!=N$,则$\exist n’\in (1,N),nn’=N$那么$n\otimes n’=nn’\ mod\ N=N\ mod \ N=0$

故选取p为素数,就是为了保证$M_6$无零因子

同时,选取一个素数作为mod值,保证了$M_7$乘法逆元:

$\forall a\in Z_p,a\otimes x=1$,即$ax\equiv 1(mod\ p)$,显然当p为一个素数时有$gcd(a,p)=1$由2拓展欧几里得定理即可求出x的值

因此$Z_p$就是一个有限域,用$GF(p)$表示

$Z_p$上的数论定理

拓展欧几里得定理求乘法逆元

int exgcd(const int &a, const int &b, int &x, int &y) {//拓展欧几里得算法ax+by=1=gcd(a,b)
	if (b == 0) {
		x = 1;
		y = 0;
		return a;
	}
	int x2, y2;
	int d = exgcd(b, a % b, x2, y2);
	x = y2;
	y = x2 - a / b * y2;
	return d;
}

int inverse(const int &a, const int &mod) {//求a在模mod下的逆元
	int x, y;
	exgcd(a, mod, x, y);
	return ((x % mod) + mod) % mod;
}

快速幂


int quick_pow(const int &base, const int &index, const int &mod) {//bash^index(% mod)
	if (index == 0)
		return 1;
	else if (index == 1)
		return base % mod;
	else if (index % 2) {
		return quick_pow(base * base % mod, index >> 1, mod) % mod;
	} else {
		return base * quick_pow(base * base % mod, index >> 1, mod) % mod;
	}
}

多项式算术

为什么突然扯到”多项式算数”呢?

前面我们证明了对于整数集$Z_N={0,1,2,3,…,N-1}$,只有当$|Z_N|=N$为素数p时,$Z_p$才为一个域

如果想要得到一个元素个数为$2^n$的域,显然$Z_p$做不到.

为什么要得到一个元素个数为$2^n$的域?计算机使用二进制编码,AES加密算法就用到了$GF(2^8)$

一个3位二进制数可以表示8中状态,明文和密码就在这八种状态之中

模8乘法	1	2	3	4	5	6	7
0	0	0	0	0	0	0	0
1	1	2	3	4	5	6	7
2	2	4	6	0	2	4	6
3	3	6	1	4	7	2	5
4	4	0	4	0	4	4	3
5	5	2	7	4	1	6	3
6	6	4	2	4	3	4	2
7	7	6	5	3	3	2	1

在$Z_8$中的数字乘法,其结果中个数字的出现次数显然是不均匀的,比如1出现了4次,2就出现了8次

而一个理想的密码是不能暴露词频信息的,显然用$Z_8$上的变换进行加密不理想,于是想一种乘法和除法的构造方法, 使得有8个元素的域其乘法或者加法的结果的频率相等

而使用多项式运算就可以解决这个问题,因此引入了多项式运算

首先要研究的是==如何构造一个有8个元素($p^n$)的域==

==将数的性质拓展到多项式式上==

我们使用的一般是代数基本规则的普通多项式运算

然后拓展到系数在$GF(p)$中的多项式运算

然后再拓展到系数在$GF(p)$,模一个$n$次多项式$m(x)$的多项式运算

最终目标是理解并应用最后一种多项式

普通多项式运算

多项式次数:最高次项的次数

多项式的表示:
$$
f(x)=a_nx^n+a_{n-1}x^{n-1}+…+a_1x+a_0=\sum_{i=0}^na_ix^i,a_n≠0
$$
如果$\forall a_i\in S$则称$f(x)$是系数集$S$上的多项式,令$<A,+,\times >$表示S上的所有多项式以及加法和乘法二元关系

当$S=Z$表示整数集的时候,显然A是满足$A_1-A_5,M_1-M_6$,是个整环,

但是不满足乘法逆元,比如$x$的乘法逆元$x^{-1}$,是一个指数为负的多项式,显然不在$A$

设
$$
f(x)=\sum_{i=0}^na_ix^i\
g(x)=\sum_{i=0}^mb_ix^i\
a_nb_m≠0,n\ge m
$$
则普通多项式的加法运算
$$
f(x)+g(x)=\sum_{i=0}^m(a_i+b_i)x^i+\sum_{i=m+1}^na_i x^i
$$
普通多项式乘法
$$
f(x)g(x)=\sum_{i=0}^{n+m}c_ix^i\
c_i=a_0b_i+a_1b_{i-1}+…+a_ib_0
$$

系数在$Z_p$中的多项式运算

当系数集是全体整数的时候,由于系数不都有乘法逆元,因此无法进行多项式除法

当系数集是一个域的时候,系数都有了乘法逆元,可以对多项式引入除法(带余除法)

可以类比整数的除法,求余数用$%$,求商用$/$

那么在$Z_p$中的多项式,求余式用$%$,求商式用$/$

比如对于$Z_2$上的多项式$f(x)=x^4+1=(x+1)(x^3+x^2+x+1)$,则$f(x)/(x+1)=x^3+x^2+x+1$

设系数域为$<Z_p,\oplus,\otimes >$

设$Z_p$上的两个多项式
$$
f(x)=\sum_{i=0}^na_ix^i\
g(x)=\sum_{i=0}^mb_ix^i\
a_n,b_m≠0,n\ge m
$$

$Z_p$多项式的四则运算

则$Z_p$上的多项式加法(减法类似)为
$$
f(x)+g(x)=\sum_{i=0}^m(a_i\oplus b_i)x^i+\sum_{i=m+1}^na_i x^i\
=\sum_{i=0}^m(a_i+ b_i)mod\ p\ \times x^i+\sum_{i=m+1}^na_i x^i
$$

$Z_p$上的多项式乘法为
$$
f(x)g(x)=\sum_{i=0}^{n+m}c_ix^i\
c_i=(a_0b_i+a_1b_{i-1}+…+a_ib_0)mod\ p
$$
$Z_p$上的带余式除法
$$
f(x)=q(x)g(x)+r(x)
$$
意思是$f(x)\div g(x)=q(x)…r(x)$

以$Degree(f)$表示多项式f的阶,并且$Degree(f)=n,\
Degree(g)=m,\$则有$Degree(q)=n-m\
Degree(r)\le m-1$

$Z_p$多项式的欧几里得定理

定义$d(x)$是$a(x),b(x)$的最大公因式,即$d(x)$是能够整除$a(x),b(x)$的所有多项式中次数最高的
$$
gcd(a(x),b(x))=gcd[b(x),a(x)%b(x)]
$$

$Z_p$上多项式再mod n次素多项式

对于$Z_p$上次数高于n-1的多项式$f(x)$,需要mod一个$Z_p$上的n次素多项式$m(x)$,如此限制$f(x)$的次数在$[0,n-1]$

什么是”素多项式”?$Z_p$上的素多项式$m(x)$无法被$Z_p$上的任意多项式整除

当$m(x)$的次数为n,则$Z_p$上的多项式$mod\ m(x)$都会落在次数小于等于n-1的多项式集$F$中

显然$F$中的多项式都可以表示为
$$
\forall f(x)\in F,f(x)=a_0+a_1x+…+a_{n-1}x^{n-1},\forall a_i\in Z_p
$$
那么这样的多项式一共有$p^n$个(系数的乘法原理),即模$m(x)$构成的剩余类

现在类比$Z_p$,证明$F$是一个域

显然加减乘封闭且结合律分配律交换律均满足,$F$容易判定为交换环

由于1也是$F$中的多项式,因此存在乘法单位元1,

下面证明M6无零因子

由于k阶多项式的k次项系数不为零,假设有两个非零多项式,其最高次项分别为$a_ix^i,b_jx^j$

乘积多项式的最高次项为$a_ib_jx^{i+j}$如果指数$i+j\ge n$则对$m(x)$取模,如果系数$a_ib_j\ge p$则对$p$取模

显然p是一个素数,$a_ib_j=a_i\times b_j$是一个合数,合数对素数取模显然不为0

因此任何两个非零多项式乘积一定非零,M6无零因子得证

到此F被证明是整环

无零因子就是$GF(2^3)$是域但是$Z_8$不是域的本质原因

下面证明任意F中的非0多项式都在F中有乘法逆元

$f(x)g(x)\equiv 1(mod\ m(x))$

$g(x)f(x)+k(x)m(x)=1$

又$m(x)$为素因式,有欧几里得定理知上式有解

因此M7乘法逆元得证

因此$F$是域

$F$和$Z_p$的不同

我们在证明$Z_p$是域的时候发现,对于整数集$Z_N={0,1,2,3,…,N-1}$,只有当$|Z_N|=N$为素数p时,$Z_p$才为一个域

而现在$|F|=p^n$显然当$n>1$时是一个合数,但是$F$仍然是一个域

将$F$记作$GF(p^n)$表示伽罗华域

$F=GF(p^n)$上的乘法逆元

$$
f(x)g(x)\equiv 1(mod \ m(x))\
g(x)f(x)+k(x)m(x)=1\
gcd(f(x),m(x))=1
$$

显然可以将整数上的拓展欧几里得推广到F上

$GF(2^n)$上构造结果分布均匀的二元运算

$GF(2^n)$上的多项式各项的系数要么是0,要么是1,可以用二进制数表示

比如$x^3+x^2+1$就可以表示为1101

加法

由于系数要么是0要么是1,即系数要自动对2取模

那么多项式的加法就是二进制数按位异或

比如$(x^3+x^2+x)+(x^4+x+1)=x^4+x^3+x^2+2x+1=x^4+x^3+x^2+1$

$01110\oplus 10011=11101$

乘法

教材上一本正经地写了一堆用字母表示的多项式,看上去头大.

从一个例子入手可能比较容易理解:

考虑AES加密算法使用到的$GF(2^8)$,取$m(x)=x^8+x^4+x^3+x+1$为模.

$f(x)=x^6+x^4+x^2+x+1$

$g(x)=x^7+x+1$

求$f(x)\otimes g(x)=f(x)\times g(x)\mod m(x)$

拆分成项

容易想到的是把$g(x)$按幂次拆分成项然后用f(x)与g(x)的各项相乘之后相加,而相加在”加法”中我们已经认识到可以通过两个多项式异或这种简洁的方式实现,因此我们现在把精力放在$f(x)$如何和一个$x^k$项相乘上
$$
f(x)\times g(x)\mod m(x)\
=f(x)\times(1+x+x^7)\mod m(x)\
=f(x)\times 1\mod m(x)+f(x)\times x\mod m(x)+f(x)\times x^7\mod m(x)
$$
问题转化为如何求$f(x)\times x^k\mod m(x)$

求$f(x)\times x^k\mod m(x)$

由于
$$
f(x)\times x^k\mod m(x)\
={[(f(x)\times x\mod m(x))\times x\mod m(x)]\times …\times x\mod m(x)}\times x\mod m(x)
$$
因此问题又可以转换为怎么跨出求$f(x)$到$f(x)\times x\mod m(x)$这第一步

求$f(x)\times x\mod m(x)$

假设$f(x)=a_7x^7+a_6x^6+…+a_1x+a_0$表示$GF(2^8)$上的任意多项式

则$x\times f(x)=a_7x^8+a_6x^7+…+a_0x$

如果用二进制表示,那么
$$
f(x)=&a_7&a_6&a_5&a_4&a_3&a_2&a_1&a_0\
x\times f(x)=a_7&a_6&a_5&a_4&a_3&a_2&a_1&a_0&0
$$
在还没有取模时,我们可以发现$f(x)$到$x\times f(x)$只需要将$f(x)$的二进制表示左移一位,下面考虑如何取模

如果$a_7=0$则$x\times f(x)$顶多是一个7次多项式,如果有$a_6=0$则顶多是一个6次多项式,一个七次多项式$x\times f(x)$去mod一个8次多项式$m(x)$实乃以卵击石,直接被8次多项式劝返

如果$a_7=1$则$x\times f(x)$与$m(x)$都是8次多项式,算是旗鼓相当,可以一战

此时$x\times f(x)$可以分成精锐的头部$x^8$与累赘的尾部$a_6x^7+a_5x^6+…+a_0x$,

这个尾部对$m(x)$取模还是被劝返,只留下精锐的头部$x^8$独自抗衡$m(x)$

那么问题转化为$x^8$对$m(x)=x^8+x^4+x^3+x+1$取模,考虑如何取模?

求$x^8 \mod m(x)$

$x^8$形单影只,只能单挑$m(x)$的$x^8$项,无暇处理$m(x)$的一伙子小弟,

于是$x^8$利用其系数都在$GF(2)$上,无中生有搬来了一伙子小弟:
$$
x^8\equiv x^8+2x^7+2x^6+…+2x+2(系数mod 2)
$$
此时用$x^8+2x^7+2x^6+…+2x+2$去$\mod m(x)$终于可以大干一场了,还得是门当户对地干,次数相同的项单挑

$x^8\equiv x^8+2x^7+2x^6+…+2x+2(系数mod 2)$作为被除数,$m(x)$作为除数,余数即为所求结果

战争一开始,商1之后被除数减去除数得到$2x^7+2x^6+2x^5+x^4+x^3+2x^2+x+1\equiv x^4+x^3+x+1(系数mod2)$

立刻发现刚才”精锐的头部”那个$x^8$在和$m(x)$的8次项的决斗中阵亡了,剩下的小弟都是7次方以下的项,无力与$m(x)$抗衡,直接作为余数

即刚才的”战争”可以写为:
$$
x^8\equiv x^4+x^3+x+1 \mod m(x)&系数mod2\
其中m(x)=x^8+x^4+x^3+x+1
$$
突然发现$x^8\mod m(x)=m(x)-x^8=x^4+x^3+x+1$

这是巧合吗?

这是系数mod2的必然结果,并且可以从8次推广到n次:

$m(x)$为n次多项式
$$
x^n\mod m(x)=m(x)-x^n(系数mod2)
$$
$x^8$独自面对$m(x)$,最终壮烈牺牲但是换回$x^4+x^3+x+1$颇有”将军百战死,壮士十年归”的感觉

在战争之前我们把”累赘的尾部$a_6x^7+a_5x^6+…+a_0x$”留下不参战,原因是他们参战也会被敌人$m(x)$直接劝返

现在我们知道了精锐的头部$x^8$和累赘的尾部$a_6x^7+a_5x^6+…+a_0x$各自参战的结果了,此时可以总结一支部队$x\times f(x)=x^8+a_6x^7+a_5x^6+…+a_0x$参战的结果了:
$$
x\times f(x)\mod m(x)=[m(x)-x^8]+a_6x^7+a_5x^6+…+a_0x
$$
比如当$f(x)=x^7+x^4+x^2+x+1,m(x)=x^8+x^4+x^3+x+1$时
$$
\begin{aligned}
&x\times f(x)\mod m(x)\
&=(x^8+x^5+x^3+x^2+x)\mod (x^8+x^4+x^3+x+1)\
&=[x^4+x^3+x+1]+[x^5+x^3+x^2+x]\
&=011011\oplus 101110\
&=110101
\end{aligned}
$$
到此我们知道$x\times f(x)\mod m(x)$如何计算了,

那么$x^2\times f(x)\mod m(x)=x\times (x\times f(x)\mod m(x))\mod m(x)$

以此类推可以得到$x^k\times f(x)\mod m(x)$如何计算了

回到求$f(x)\times g(x)\mod m(x)$

不管你$g(x)$长什么样,我先预处理出$f(x)\times x\mod x,f(x)\times x^2\mod m(x),f(x)\times x^k\mod m(x)$等等情况

如果你$g(x)=1+x+x^2$长得很虚,那么
$$
f(x)\times g(x)\mod m(x)\
=f(x)\times (1+x+x^2)\mod m(x)\
=(f(x)+x\times f(x)+x^2\times f(x))\mod m(x)\
=f(x)+x\times f(x)\mod m(x)+x^2\times f(x)\mod m(x)
$$
直接利用预处理得出的结果,然后计算加法直接用二进制异或

总结

到此我们构造出了$GF(2^n)$,即有$2^n$个元素的伽罗华域

怎么构造出的?由系数在$GF(2)$上的多项式模一个$2^n$次的素多项式拓展出的

多项式和这$2^n$个数怎么产生联系?每一个多项式都对应一个二进制数

这$2^n$个数的加减乘除运算怎么定义的?还是通过多项式的运算得到的

下一步可以向AES加密算法进军了

模8乘法	1	2	3	4	5	6	7
0	0	0	0	0	0	0	0
1	1	2	3	4	5	6	7
2	2	4	6	0	2	4	6
3	3	6	1	4	7	2	5
4	4	0	4	0	4	4	3
5	5	2	7	4	1	6	3
6	6	4	2	4	3	4	2
7	7	6	5	3	3	2	1

模8乘法	1	2	3	4	5	6	7
0	0	0	0	0	0	0	0
1	1	2	3	4	5	6	7
2	2	4	6	0	2	4	6
3	3	6	1	4	7	2	5
4	4	0	4	0	4	4	3
5	5	2	7	4	1	6	3
6	6	4	2	4	3	4	2
7	7	6	5	3	3	2	1

模8乘法	1	2	3	4	5	6	7
0	0	0	0	0	0	0	0
1	1	2	3	4	5	6	7
2	2	4	6	0	2	4	6
3	3	6	1	4	7	2	5
4	4	0	4	0	4	4	3
5	5	2	7	4	1	6	3
6	6	4	2	4	3	4	2
7	7	6	5	3	3	2	1