机器级算术运算的原理
落脚在加法,全加器,半加器,全加器级联,等最基础的知识
机器在算术的时候有很多行为和人不一样,但是权位的思想是相同的
人在算术的时候通过列竖式对其的方式,隐含着权位规则.
机器将权位规则体现在,随着运算会有中间结果的位移
理解了机器将中间结果移位的原因,也就理解了机器级算术运算的原理
计组第三章讲的机器机计算方法实际上和程序员距离比较远,ALU中已经封装好了各种计算方法,那为什么还要我们学这一部分呢?
我的感觉让我们是理解计算机底层实现中的状态机思想,
在推导适应机器的算法时,越发感觉出,有固定的状态的转移套路
而这种思想将对我们在开发状态机服务端的时候提供世界观上的支持
然而课本对于该部分的介绍基本止步于如何计算,并没有下到算法如何设计得到的,可以说是一大遗憾.
现在将我的设计和课本给出的设计思想其补上
手算原码乘法
这是万恶之源,通过一个例题观察人类对权位规则的应用

之前一直不知道怎么描述这个过程,只能是手写比划比划,直到看了CSAPP第二章位向量表示法,终于知道怎么描述这个过程了
只看小数点后面的部分,把$X,Y$表示成位向量,有
$$
X=[X_3X_2X_1X_0]=\sum_{i=0}^3[2^i\times X_i](X_i=0\ or\ 1)
$$
$$
Y=[Y_3Y_2Y_1Y_0]=\sum_{i=0}^3[2^i\times Y_i](Y_i=0\ or\ 1)
$$
那么手算的思想可以用下式表示:
$$
\begin{aligned}
ANS&=X\times Y\
&=X\times\sum_{i=0}^3[2^i\times Y_i]\
&=\sum_{i=0}^3[ 2^i\times X\times Y_i]\
&=[X\times Y_0]+2[X\times Y_1]+4[X\times Y_2]+8[X\times Y_3]\
&=A_0+A_1+A_2+A_3\
&=E\
&=[E_3E_2E_1E_0]
\end{aligned}
$$
其中
$$
A_i=2^i\times [X\times Y_i],i\in[0,3]
$$
$$
E_j=\sum_{i=0}^3A_{ij}+低位进位\
j\in[0,7]\
$$
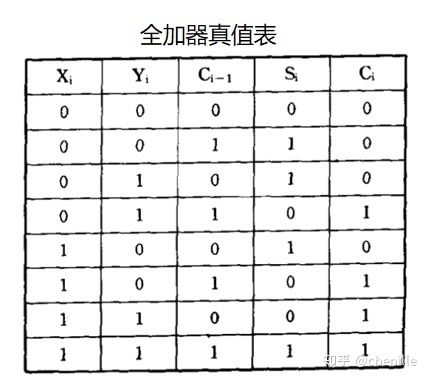
这里$E_i$的计算方法就是小学里算竖式的时候,老师常说的”落下来”
从图上我们可以更清晰地看出,被乘数分别和乘数的”个十百千位”相乘,按位对其之后落下来累加得到E
原码一位乘法
如果让机器原封不动重复刚才手算的过程
替机器瞎操心
他需要维护一个二维数组,记录用X和Y的每一位相乘,分别得到的中间位向量$A_i$
然后”落下来”求$E$
就这个二维数组就把机器难为住了
1.如果两个32位整数相乘,就需要32*32个方格的二维数组,ALU可是没有记忆功能的,寄存器也就稀松几个,记忆能力有限,显然32²个方格没处放.
2.机器怎么知道当前应该用X对齐Y的”个位”还是”十位”还是”百位”呢?用一个寄存器,记录Y已经被对齐过几位吗?
不需要,因为本次对齐的位一定是只比上一次对齐位高一位,只需要将被乘数左移一下.
然后根据本次Y的对齐位是1则$Ai=X\times 权重$,比如图表中$A_3$
如果本次Y的对齐位为0则$A_i=0$,比如图表中$A_2$
问题又来了,权重用谁来记住呢?再开一个寄存器,初始记录1,表示权重为$2^0$,随着被乘数$X$的左移,这个寄存器也要左移一下表示权重乘以2
如果继续研究如何让硬件实现,还能发现更多问题.第一,机器算账,这钱怎么进了你自己的腰包
滚动数组
现在考虑一下,有必要维护这个二维数组吗?滚动数组行吗?
中间过程不使用二维数组,就维护一个位向量$A$,计算过程中A只有累加和右移两种行为.
乘数个位为1,则被乘数直接加到A的高四位
为啥是高四位呢?似乎有点违反直觉,因为A的高位表示的是高权重,但是现在用被乘数乘的是乘数的个位,权位最低才对啊.别忘了A要右移
然后A右移一位,乘数右移一位
这个过程干了一个啥事呢?
被乘数一直和乘数的”最低位”对齐,刚才最低位是”个位”,现在经过右移,个位直接扬了,十位成了”最低位”.被乘数时钟看乘数最低位脸色行事,当这个最低位是1的时候才把自己加到A上,加到A的最高四位上
A右移一位,则所有历史记录都降权2,
可想而知,当乘数的千位右移到最低位,这时候被乘数将自己加到了A的高四位上,此时计算结束.乘数的千位和被乘数的积 的权就最高,根本不需要降权
而乘数的个位和被乘数的积此时已经经历了4次降权,权重仅为$\frac{1}{2^4}=\frac{1}{16}$
这正好满足我们的目的
现在可以用机器实现了
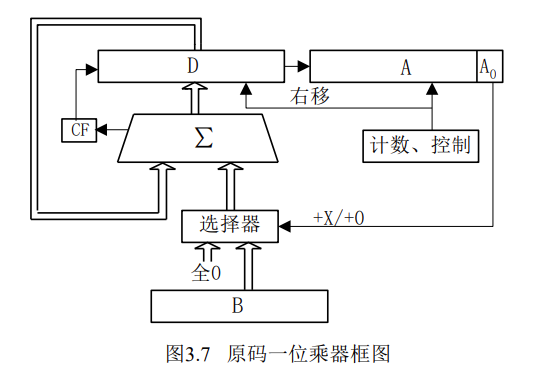
硬件框图的意义
这个图怎么看呢?
D和A合起来作为”中间过程位向量”,D就是高四位,A就是低四位
一开始的时候D=0,A=Y,这好像和我们刚才的分析不一样,我们分析的滚动数组思想中,Y是独立存在的,不会放在A中.
而实际上Y需要独立存在吗?考虑每次被乘数要么不加,要么加到高四位上,而Y一开始放在低四位,两者不会相互影响.
随着这个中间过程位向量不断右移,Y被一位一位移除了A,当Y恰好移出的时候计算恰好结束.
$A_0$就是乘数的”最低位”,随着乘数Y的不断右移,硬件A的最低位会以此存放Y的个十百千位,相当于将Y遍历了一遍
“被乘数看乘数最低位颜色决定加不加”这个事怎么实现的呢?
用一个B寄存器存放被加数X,X和0作为二选一选择器的数据段,$A_0$作为该二选一的地址端,当$A_0=1$则选通X,当$A_0=0$则选通0
选通的信号就进入了$\Sigma$多位加法器
左上角这个循环干了啥事呢?
被加数总是加到中间过程位向量的高四位,这怎么实现?将旧的高四位作为加数和X相加就得到了新的高四位
这个半调子CF是干啥的呢?
CF是PSW程序状态字中的一位,用来记录是否有进位,啥时候会有进位呢?
比如头一次D=1111,右移变成0111,然后下一次又加了1111,显然0111+1111溢出了,但是顶多溢出一位,于是放到CF里,然后D右移的时候,再从CF里拿出来放到D里
手写模拟
模拟机器计算$0.1101\times 1.1011$(都是原码)
符号显然同号得负数,这对机器来说也是小菜一碟,两符号娶个异或即可
去掉小数点,后面的直接作为整数乘法,怎么乘的呢?
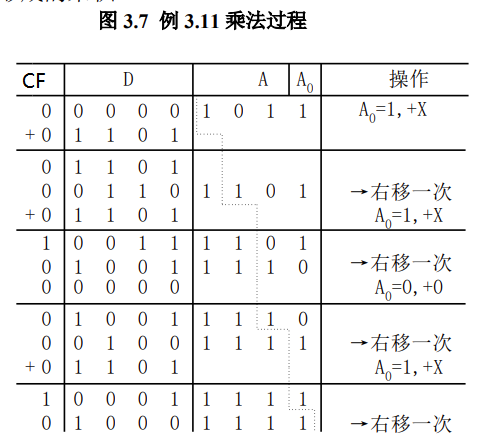
最左侧这里列也是有实际意义的,里面是CF位的状态.
这一点课本并没有给出,这导致我一开始认为只有手算模拟才会用到这一列
乘数有四位,因此共有四次操作,恰好将Y从A中扬了,中间结果积逐渐充斥整个D和A
这个过程要是找个现实中的类比的话,可以举这么一个不恰当的例子:
一个公司有10个部长,资本家的总是嫌这十个人好吃懒惰不干活,或者说即使比较勤奋,但是不想再给他发太多工资,直接降薪吧人家也不愿意.反正就是想找个理由踢了这是个人换成新人
但是资本家还不敢一口气全体了,这会造成一段时间没人管事儿.
于是资本家想了一个温水煮癞蛤蟆的方法,每隔一个月从这10个人里找一个业绩最差的,
要是他真的好吃懒惰啥也不干,直接踢了,公司正常运转.
要是他确实负责一些事情,那么找一个能干的新人把他挤了,公司正常运转
10个月后,10个部长就全是优秀并且高效的00后了
无符号右移?
关于”无符号右移”,这个事情发生在

| 原数 | 带符号右移结果 | 无符号右移结果 |
|---|---|---|
| $1’0011’1101$ | $1’1001’1110$ | $0’1001’1110$ |
显然正确的计算方法是无符号右移,为啥不是带符号的呢?
首先,带符号意味着负数,而我们整个计算过程中要么加0,要么加x,反正不会加一个负数,理论上就不存在加负数的情况
再者,这里最左侧的”符号”实际上是CF位,是上一次加被乘数之后的进位,不是”符号”,我们一直在进行无符号运算
原码两位乘法
为啥要两位乘?
原码两位乘法和原码一位乘法的思想基本相同,但是设计硬件的那伙子人嫌一位乘法太慢,这就好比一个人上楼梯,每次上一个台阶嫌慢,非得上两个
为啥没有原码三位乘法?一次上三个台阶这不扯蛋吗
因为计算机中的数据都占用偶数位,从来没有说有一个66位计算机,有一个63位计算机,有一个30位计算机.
实际存在的计算机都是64位,32位,这些位数都是2的幂次,为啥非要是2的幂次?方便使用二进制呗.为啥一定使用二进制?逻辑门高电位和低电位就两种状态呗
为啥没有原码四位乘法?32和64不也是4的倍数吗?
还要考虑一个复杂性问题
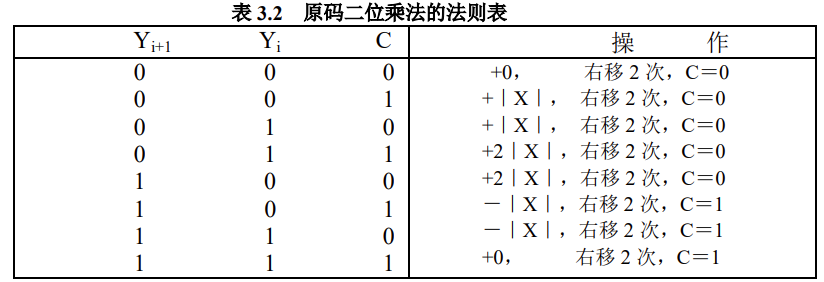
如图原码二位乘已经有$2^3=8$种情况了,要是原码四位乘,不考虑低位进位的情况至少这四位需要考虑,就已经有$2^4=16$种情况了,显然让ALU考虑多种情况也是需要记忆功能的
在记忆能力和速度都可以接收的范围内,只有原码一位乘和原码二位乘是可行的
规则
两位乘怎么玩呢?
原来被乘数看乘数最低位的脸色行事,现在被乘数还要看次低位的脸色.真的太卑微了
最低位和次低位的权还不一样,次低位更狠,权更重.
为了更详细的描述这个意思,规定X和Y的位向量表示
X和Y都忽略小数点和符号位,小数点后面的直接作为一个整数
$X=X_3X_2X_1X_0$
$Y=Y_3Y_2Y_1Y_0$
现在最低位就是$Y_0$,次低位就是$Y_1$,随着Y不断右移,这两个位会遍历整个Y
当$Y_1Y_0=11=3(Dec)$需要向中间过程位向量上加三个被乘数X,
当$Y_1Y_0=10=2(Dec)$需要向中间过程位向量上加两个被乘数X
当$Y_1Y_0=01=1(Dec)$需要向中间过程位向量上加一个被乘数X
当$Y_1Y_0=00=0(Dec)$啥也不加
啥也不加,加一个X都好说,加两个X通过将X左移一位×2也容易实现,但是这个半吊子3怎么办呢?
3=4-1,啥意思呢?
先从中间过程位向量的高四位减去一个被乘数X,
然后右移两位,这导致刚才减去的X降权4(右移两位相当于除以4),
此时再向高四位加上一个被乘数X,这个刚加上的X的权就高,是刚才减去的X的四倍,
这样一减一加,相当于在上一步(刚才减一的那一步)往中间过程位向量上加上了3个X.
达到了我们的目的
当$Y_1Y_0=11$,这时候才会加3X,还有加2X,1X,0的时候,怎么区分多种状态呢?用一个flag开关
也就是下表中的C
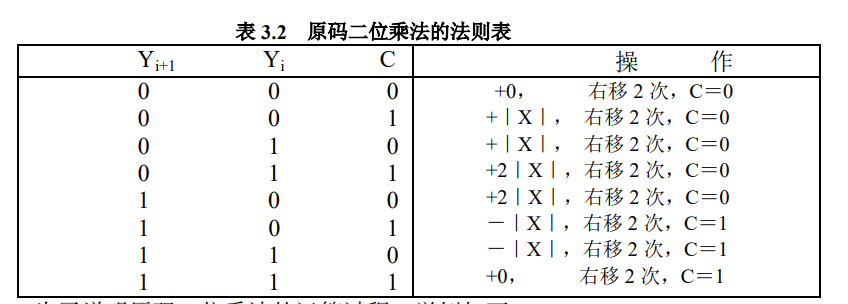
这个表什么意思呢?
我一开始的理解
(当然是错误的,但是有借鉴意义)
刚才我们推导怎么实现加3X的时候,先减X,位移后再加上X,看上去顺理成章,确实解决了上一回合需要加3X这个问题,
但是同时引入了新问题,即
位移后的本回合有本回合要做的事情,而你却在本回合处理了上回合要做的事情,那么本回合本来要做的事情啥时候做呢?
啥叫本回合应该做的事?
每个回合要做的事就是根据当前乘数最低两位的脸色决定往中间过程位向量上加几个X
要么本回合开一个额外回合,在给上回合擦腚之后,先不忙着将乘数右移开启下一个回合,而是正式处理本回合的事.处理完了再右移开启下一回合
但是这样怎么让一个傻子CPU知道这一次有没有额外回合呢?
可以用标志位C.每个正式回合都根据乘数最低两位是否全1,设置C是否为1,
当回合开始的时候,让CPU先检查C开关是否打开,
如果开着则先擦腚,然后C给他关上,
如果C关着(不管是本来就管着还是擦完腚关上的,一视同仁),则处理本回合事物
我确实一开始是这样想的,但是仔细观察法则表之后发现人家的想法和我不一样
人家的想法
如果按照我的设想,当C为1的时候,不需要看$Y_1Y_0$的脸色,直接加X,然后C置零
然而表中即使C为1也需要看$Y_{i+1}Y_{i}$的脸色
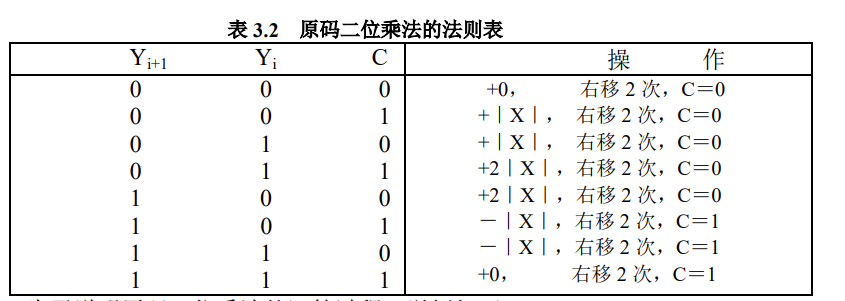
那么人家的方法什么思想呢?

这段文字十分滴珍贵,但是是那种懂的人一看就懂,不懂的看了还是不懂(此名言出自计组老师gx)
啥意思呢?不妨从研究这个表的结构规则入手
可以发现,
1.当$Y_{i+1}$固定时,$Y_i$和$C$具有对称结构,具体表现为:
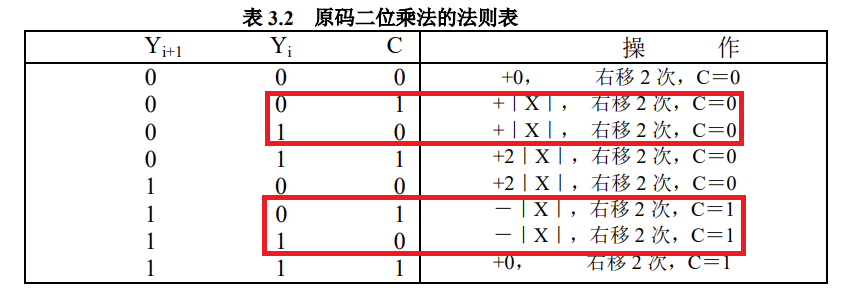
2.$Y_i$和$C$联手的时候相当于$Y_{i+1}$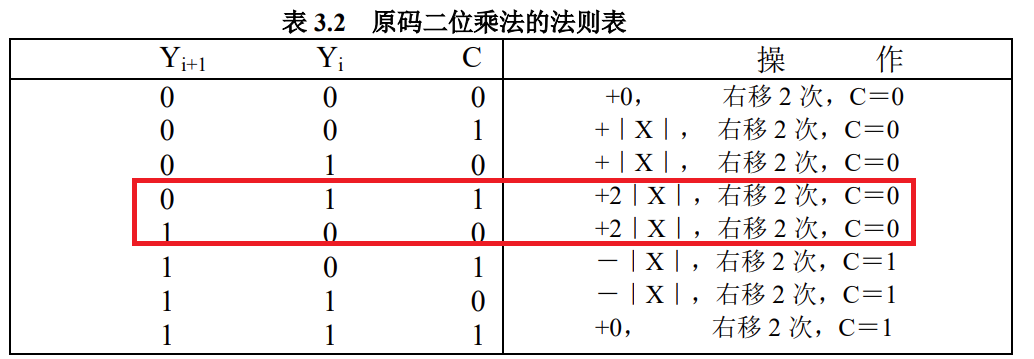
也就是说,$Y_i$和$C$就有完全相同的地位,$Y_{i+1}$权为2, $Y_i$权为1,$C$的权也是1
而这种类似的结构我们在什么地方见过呢?全加器
全加器中$X,Y,C_{i-1}$三者具有轮换对称结构
而$C_{i-1}$表示的是低位向本位的进位开关,类比到原码两位乘法中,他就是低位计算时没擦干净的屁股
在这个全加器运算的时候,会同时考虑三路输入,将$X_i,Y_i,C_{i-1}$同时加起来,也就是在完成本回合的事物时,同时把上回合的屁股擦了
但是也可以设计成,$X_i+Y_i$先算好,然后将上回合的屁股$C_{i-1}$加上
设计固然可以这样设计,但是何必呢?算好的结果还需要保存一下然后才和$C_{i-1}$相加.
直接三个加起来不用保存中间结果并且更容易实现,岂不美哉
就用全加器的思想考虑在原码两位乘法
C不也是低位向本位的进位吗?或者说,上一个回合留到本回合才能擦干净的屁股
在上个回合加4X,不就相当于在本回合加X吗?
处理上回合的屁股顶多在本回合加一个X,
要是本回合本来啥也不干,那么处理屁股,加上X就完了

要是本回合本来就应该加X,那么一块处理了,加上2X就完了

要是本回合本来应该加2X,加上屁股一个X,一共3X,只需要减一个X然后继续把屁股交给下一个回合

要是本回合本来应该加3X,加上屁股一共四个X,可以加上左移两次的X,但是留一个屁股给下一回合加上也是相当于本回合加4X,还不用位移,岂不美哉
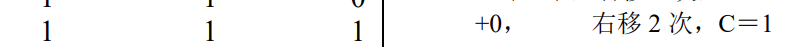
如果上个回合没有留屁股(即C=0),则本回合只需要看$Y_1Y_0$脸色行事,不用擦屁股
如此这个法则表就不用死记硬背了
手写模拟
$X=+0.100111,Y=-0.100111$用原码两位乘法求积
符号显然为1
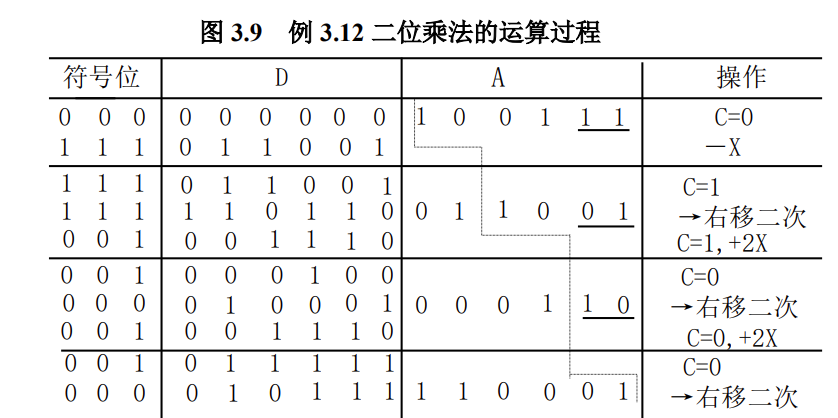
这个”符号位”是啥呢?
这确实是符号位,因为过程中有$-X$的行为.为啥要三个符号位呢?这个是人为规定的
因为两位乘每回合需要右移两位,那么符号位至少有两位,至于为什么是三位呢?
因为存在带符号右移的行为,右移两位之后符号位高两位是填充0呢还是填充1呢?
能不能全都填充0呢?诚如是则三个符号位都是摆设,编课本的人也不用编了.多此一举何必呢?
这符号位的最高位起一个提示的作用,如果最高位为1则右移的时候最高位也补1,否则补0
因此最高位完全是个人爱好添加的,因为只要是最高位是1,则符号位的第二位也是1,完全可以根据第二位的提示填充符号位的高两位
这里就有问题了,为什么会有带符号右移?原码一位乘法的时候明明没有带符号右移啊?

因为过程中确实有$-X$这种行为,通过加补实现,而补码的符号位就是负数.
如果无符号右移,则本回合$-X$在右移后进入下回合时,符号位也跟着移到右侧,这个$-X$成了加一个数,失去减法的意义并且导致错误
补码一位乘法–布斯法
推导算法原理
令$X=X_0.X_{-1}X_{-2}…X_{-(n-1)}$,$Y=Y_0.Y_{-1}Y_{-2}…Y_{-(n-1)}$
将$Y$按照权位展开
$$
\begin{aligned}
Y&=Y_0.Y_{-1}Y_{-2}…Y_{-(n-1)}\
&=Y_0\times 2^0+Y_{-1}\times 2^{-1}+Y_{-2}\times 2^{-2}+…+Y_{-(n-1)}\times 2^{-(n-1)}\
&=Y_0(2^1-2^0)+Y_{-1}\times(2^0-2^{-1})+Y_{-2}\times (2^{-1}-2^{-2})+…+Y_{-(n-1)}\times (2^{-(n-2)}-2^{-(n-1)})\
&=2Y_0+2^0(Y_{-1}-Y_0)+2^{-1}(Y_{-2}-Y_1)+2^{-2}(Y_{-3}-Y_{-2})+…+2^{-(n-2)}(Y_{-(n-1)}-Y_{-(n-2)})+2^{-(n-1)}(0-Y_{-(n-1)})
\end{aligned}
$$
其中$Y_0$是符号位,当$Y_0=0$,$2Y_0=0$,可以忽略
当$Y_1=1$,$2Y_1=10$进位不管,本位还是$0$,也可以忽略
那么$Y=2^0(Y_{-1}-Y_0)+2^{-1}(Y_{-2}-Y_1)+2^{-2}(Y_{-3}-Y_{-2})+…+2^{-(n-2)}(Y_{-(n-1)}-Y_{-(n-2)})+2^{-(n-1)}(0-Y_{-(n-1)})$
不妨令$Y$最后再加一位$Y_{-n}=0$反正小数部分最后添0不会影响小数大小
那么
$$
\begin{aligned}
Y&=2^0(Y_{-1}-Y_0)+2^{-1}(Y_{-2}-Y_1)+2^{-2}(Y_{-3}-Y_{-2})+…+2^{-(n-2)}(Y_{-(n-1)}-Y_{-(n-2)})+2^{-(n-1)}(Y_{-n}-Y_{-(n-1)})\
&=\sum_{i=-(n-1)}^{0}2^{i}\times (Y_{i-1}-Y_i)
\end{aligned}
$$
好了,现在$Y$经过各种调教,已经连同符号位都可以一起计算了
$$
\begin{aligned}
X\times Y&=X\times \sum_{i=-(n-1)}^{0}2^{i}\times (Y_{i-1}-Y_i)\
&=\sum_{i=-(n-1)}^{0}[2^{i}\times (Y_{i-1}-Y_i)\times X]
\end{aligned}
$$
这是一种啥形式呢?每次$X$都看$Y_{i-1}Y_{i}$的脸色行事,$2^i$是这俩哥们儿的权重.此时不再考虑$Y_{i-1},Y_{i}$的权重区别了,因为$2^i$是两个家伙的共同的权重,两者权重的二倍关系,已经应用在在刚才的转化过程中
| $Y_{i-1}Y_{i}$ | $Y_{i-1}-Y_{i}$ | 行为 |
|---|---|---|
| 00 | 0 | 啥也不干 |
| 01 | -1 | -X |
| 10 | 1 | +X |
| 11 | 0 | 啥也不干 |
在一个回合内应该干的事情:
从$i=-(n-1)$这个最低权位开始算,每次根据$Y$的最低两位确定行为,然后右移一位,将$Y_i$移出扬了,刚才的$Y_{i-1}$现在是最低位.
每个回合开始前,将上回合的中间过程位向量右移一位,作用是给先前的计算结果都降权2
硬件实现
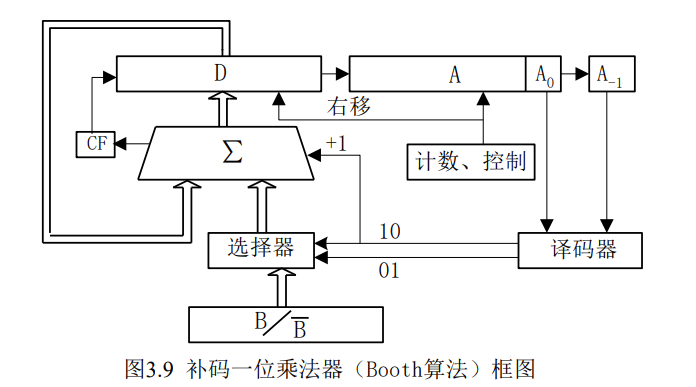
这个图应该怎样理解呢?
D和A两个寄存器共同组成中间过程位向量,最右边有一个$A_{-1}$是附加位,这个刚才我们也分析过了,小数部分最后随便添0不影响结果大小
一开始的时候,乘数$Y$符号位和数值位都放在A中,小数点扬了,$Y$的最低位落到$A_0$,此时$A_{-1}=0,D=0$
右移的时候$A_{-1}$也要参与,刚才的$A_0$就移入$A_{-1}$,一共右移多少次呢?将A中的乘数刚好扬了为止,比如$Y=1.0011$则右移5次(符号位和数值为没有区别)
$A_0A_{-1}$接入一个二四译码器,而实际上一共有三种情况,啥也不干,+X,-X,怎么把这三种情况转化成机器能听懂的语言呢?
当$A_0A_{-1}=00$则选择器选通$D_0=0$
当$A_0A_-1=01$则选择器选通$D_1={B}$
当$A_0A_{-1}=10$则选择器选通$D_2=\overline {B}$,此时$A_0\overline A_{-1}$接入与门,与门接到全加器最低位,作用是对$B$的取反再+1得到补码
当$A_0A_{-1}=11$则选择器选通$D_3=0$
选通信号都输入全加器
中间过程位向量$[D:A]$在右移的时候带符号右移,即$CF$跟着移入最高位,并且右移之后$CF$状态不变
手算模拟
$X=0.1010,Y=-0.1101$,计算两个数的补码一位布斯乘法
$[X]_补=00.1010$
$[Y]_补=11.0011$

最终没有特判符号位,而是符号位已经在CF中了
经过刚才的分析,现在$A_{-1}$就具有实际意义了,不再是一个根据人的意愿补上的一位了
每个回合,被乘数都根据$A_{0}A_{-1}$的脸色行事,比如当$A_0A_{-1}=10$时,应该-X
而这似乎和我们一开始推导算法的时候相反

我们推导的是当$Y_{i-1}Y_i=10$时+X
实际上令i=0得到$Y_{-1}Y_0=10$调个个儿就得到$Y_0Y_{-1}=01$
因此$A_{0}A_{-1}=10$实际对应的是$Y_{i-1}Y_i=01$的情况,行为是-X
这里一定要分清关系
在手算模拟的时候,只需要用$A_{-1}-A_0$,根据结果的正负决定加减X,$A_{-1}-A_0=1$则+X
关于手算时符号位为啥要两位?
实际上机器只需要一位,这一位就有实际意义,即CF的值
然而由于计算过程中需要带符号右移一位,这样符号位是11时右移一位变成01,我们模拟时一看符号位还有1,于是高位填充1,修正成11
即最高位是防止人计算的过程中犯糊涂用的
并且符号位两位起到了双符号位判断溢出的作用,如果计算过程中,出现了两个符号位不同的情况,啃腚是算错了
原码除法
手算
约定规则

这个规则第一条我就绷不住了,就算是两个定点纯小数,被除数的绝对值也不一定比除数小吧,比如$0.1111\div 0.0111$,整数也是如此
那为啥要这样规定呢?为了保证两个定点纯小数的除法结果还是一个定点纯小数,
一旦被除数的绝对值大,则至少结果的整数部分可以商出一个1来,这时候运算结果就是定点既有整数也有小数了
而我们希望的是不使用整数部分,硬件上根本就不允许整数部分有意义,而是只保留小数部分
比如$0.1111\div 0.0111=1.00010001..$
而硬件是这样计算的:$1111\div 0111=00010001$,因为硬件就认为这个结果只可能是小数
下面通过列竖式的方法计算$X=0.1011$,$Y=0.1101$两数的除法,推导适用于机器的算法

由于已经保证被除数绝对值小,因此结果的整数个位必定商0
人类在计算竖式的过程中有一个特点—人类会试商,啥意思呢?
在商了前两个1之后,下面要计算$1010\div 1101$,
人类一看除数大,商1就过分了,剪出来一个负数,因此人类此时会商0.
试商我们从小学就学过了,那时候是在十进制下,每次试商都要按照9,8,7,…,2,1,0这种顺序试商(熟练了可以用二分结果试商),直到试到某个值n,此时用n去乘被除数得到的积刚好比中间结果小或者相等整除,并且商$n+1$刚好比中间结果大,那么n就是该位应该上的商
而现在对于二进制,每一位只有两种状态0或者1,我们只需要试商1,成功则商1,失败则商0
本质思想是相同的,只不过二进制中商0和商1是相互对立事件,而十进制中商0和商1是互不相容事件,因为十进制下还可以商2,3,等等
然而机器怎么试商呢?机器进行的每步运算都要改变硬件状态,试商会直接把商写进中间过程位向量,他只有一次机会,不允许试.而人类可以在草稿上试商然后将准确的商写道卷子上
恢复余数法
虽然机器不能试商,但是机器可以知道的是,自己尚一个1,有没有商的太过分了,
商1,则用中间结果去减被除数,如果减出来结果是个负数,机器就能根据符号位知道发生了什么.
他知道刚才商的太狠了,本应该下手轻点的.
于是他可以反悔,刚才商1导致中间结果负了,那么现在改商0,中间结果再加一个被除数还原到商1之前的情况,刚才商的1不算数.这个过程叫做”恢复余数“
手算模拟$X=-0.10001011除以Y=0.0110$的过程
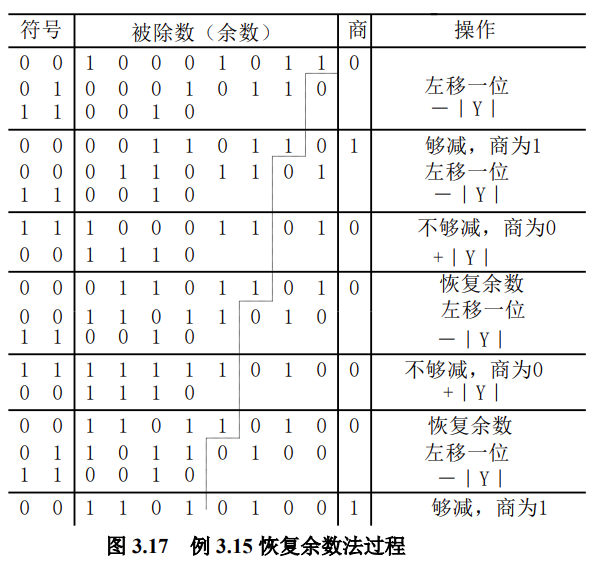
最终结果咋看呢?
看最后一行,
商的绝对值是$0.1001$,最前面这个0肯定是0,这就是整数位个位的商,由于被除数比除数小,因此这一位必定为0,商的结果根据除数和被除数的符号位异或决定,因此商是$1.1001$
余数的绝对值是$0.1101\times 2^{-4}$,符号应该和商一致,因此余数是$1.1101\times 2^{-4}$
这里$2^{-4}$怎么来的呢?余数实际上是中间过程位向量最开始时的低四位经过运算和左移得到的,其本来的权就是$2^{-4}$
为啥乘法的时候需要中间过程右移,而除法的时候需要中间过程左移呢?
在做除法的时候我们都是从高位往低位商,而做乘法的时候是从低位向高位乘,两种运算的顺序相反
做除法时早商应该比晚商权重高,通过左移,越早的商越高,权重越大
从图上可以发现一个问题,够减的时候,中间结果左移,不够减的时候,恢复余数,不左移
怎么让机器知道够不够减?前面分析的是根据符号位.
确实根据符号位可以知道这个事情,但是知道了怎么处理呢?
哪个元件可以根据CF的状态,决定给ALU送什么数呢?这个过程对硬件来说太抽象,不容易实现
想法总是千奇百怪,但是真到落地实现的时候,直接摔死
这让我想到大二上学微信小程序的时候,我竟然痴心妄想整一个支持markdown,用缩进表示分支的思维导图(Flowchart).属实是高估自己的编程能力和知识储备了
然而本学期tx学写游戏的时候,一些听上去天马行空的事情,都被库函数实现了,只能说,人定胜天
加减交替法
由于恢复余数法不方便实现,考虑一个让硬件舒服的方法
还是从恢复余数法中吸取教训
不妨定义一个说法”回合”,感觉这像是一个状态机
每一回合都要经过,恢复余数(这算是上回合留下的屁股),左移一位,上本次的商,这几个过程
如果上回合留下了一个屁股,即上回合商1导致中间过程负了,本回合需要首先加上被除数恢复余数,并且上回合的商1作废,改为0,然后左移一位,让上回合的商升权2,然后直接商1,把屁股留给下一个回合
如果上回合没有留下屁股,即上回合商1,中间过程减去被除数得到正数,则不需要恢复余数,直接左移让上回合的商1升权2,然后直接商1把本回合的屁股留给下一个回合
好的, 现在考虑,
本回合需要处理上回合的屁股,首先R(中间过程结果)+Y(被除数),
然后左移一位,$2(R+Y)$
然后处理本回合事物,直接商1有$2(R+Y)-Y=2R+Y$
这不就相当于刚才不擦屁股,直接余数R左移,然后加上Y吗
本回合不用擦上回合的屁股
直接R左移一位变成2R
然后处理本回合事物,直接商1有$2R-Y$
综上,每个回合要么$2R+Y$,要么$2R-Y$,总共两种状态,
通过中间过程符号位决定本回合采用哪种状态
啥时候上商呢?在回合开始还没有位移的时候,根据中间过程的符号上商,
中间过程符号为0则商1,中间过程符号为1则商0
这就好实现了,
2R相当于本回合上来就中间过程左移,
中间过程符号位作为地址端接到2选1选择器,
符号为1则$-Y$选通,并且还要向ALU最低位加一个1,实现加补操作
符号为0则$+Y$选通
硬件实现如图
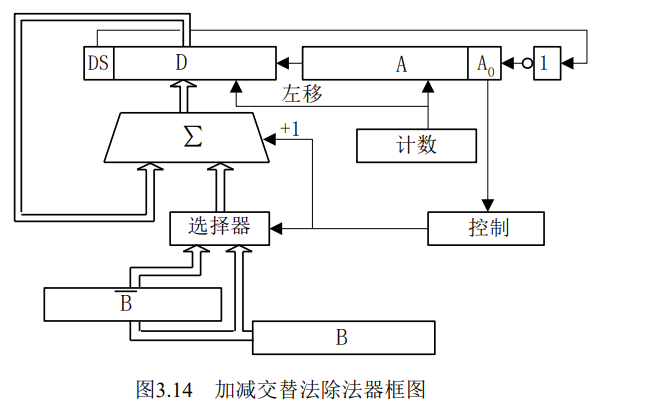
怎么解读这个框图呢?
以$X=-0.10001011,Y=0.1110$为例,
$|X|=0.10001011,|Y|=0.1110$
一开始$|X|$放在D和A中

第一回合,本回合比较特殊,当前中间过程就是被除数(绝对值),符号为正,但是商0
然后左移,刚才的符号位0取反后移入$A_0$,$A_0=1$决定本回合-Y,即加Y补
得到新的中间过程
如下图描述

第二回合,当前中间过程为$00’00110110’$,符号为正,商1
左移一位,符号位0取反之后移入$A_0$,$A_0=1$决定本回合$-|Y|$,即加补
得到新的中间过程
如下图描述

第三回合,当前中间过程为$11’10001101$,符号为负,商1
左移一位,符号位1取反得0之后移入$A_0$,$A_0=0$决定本回合应该$+|Y|$
得到新的中间过程
如下图描述

以此类推
最终结果怎么看呢?
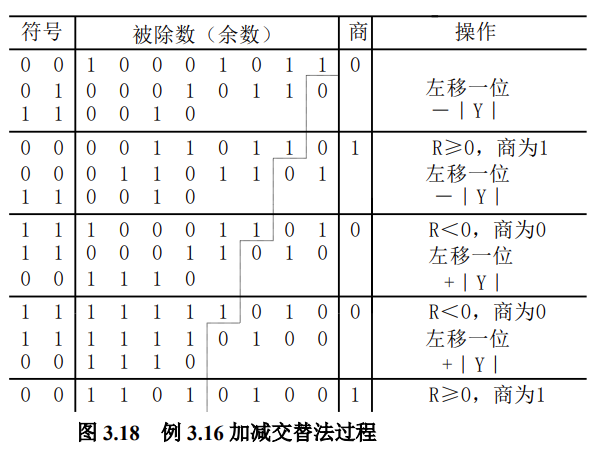
商这一列从上到下就是商,最上面这个0不用管,每次都是0,原因是我们故意控制被除数绝对值比除数小
或者看最下面这一行最右边01001,就是商这一列不断右移得到的
余数绝对值$0.1101\times 2^{-4}$,符号和商相同,都要看被除数和除数的符号异或
补码除法
这句话我看了好半天才看明白,
“与乘法运算的情况类似,有时也会迂回到补码乘法”
好家伙算个数还有迂回战术,就gx那三眼一板,一丝不苟的治学态度,我不大相信他能整出这样的词儿来
看了好几遍发现没有”回”,就一个”迂”,
是在说用补码做除法的人都迂吗?想到这里我都笑出了声,
用迂字骂人真有感觉,尤其和13合起来,”迂13!”,这山东话绝对有气势
巧了宿舍群就这样命名的
应该是错字,本来想用”用”字的
绷不住了
补码除法状态机
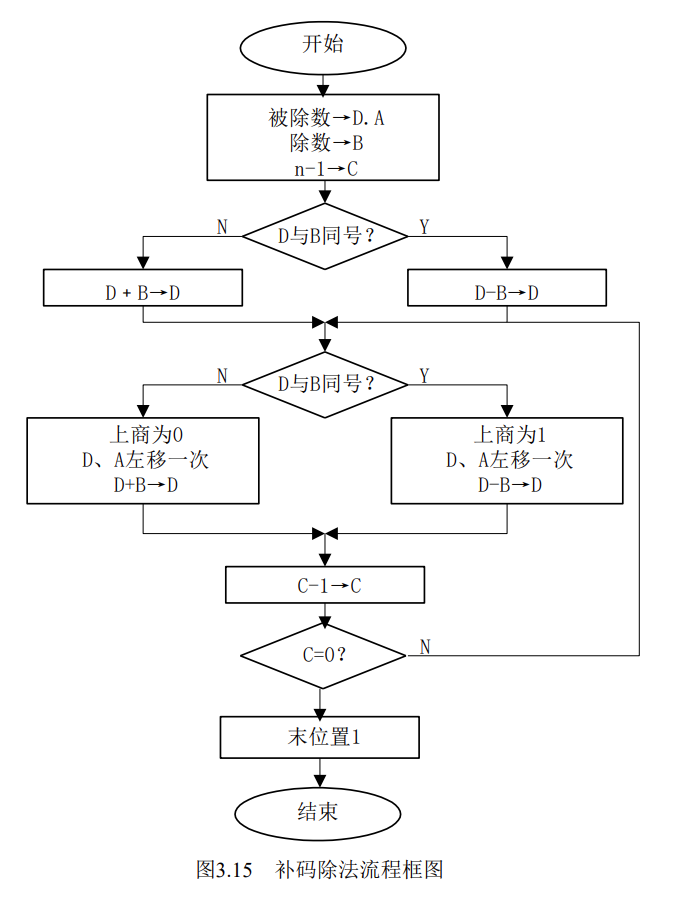
状态就是被除数或者说余数,或者说中间过程位向量的符号状态,所有的状态转移都是根据该符号位决定的