傅里叶变换
一个欠了一年的帐,今天终于还上了
我根本不知道录音的基本原理
$O(n\lg n)$内求解多项式乘法
算法导论上的傅里叶变换,是为了在$O(n\lg n)$时间内,解决多项式乘法
如果直接让两个多项式卷积,那么朴素方法复杂度显然是$O(n^2)$
如何降复杂度呢?使用点值计算
线性代数上可以证明,一个n-1次多项式,可以在其图像上使用n个点唯一确定(插值方法)
也就是说,一个多项式$A(x)=\sum_{j=0}^{n-1}a_jx^j$可以用n个点表示
那么两个均为$n-1$次的多项式$A(x),B(x)$,其乘积多项式就得是一个$2n-2$次多项式,需要$2n-2$个点唯一确定
显然从一个$n-1$次多项式上取n-1个点已经足够唯一确定这个多项式了,再取其他点就是冗余信息,对确定表达式没有影响,因此可以在$A(x),B(x)$上各取2n-2个点,计算这2n-2个点的积,这就得出了积多项式的点值表示
其中第i个点$C(x_i,A(x_i)\times B(x_i))$纵坐标为两个多项式在$x_0$处函数值的乘积
画在图上也就是:
普通乘法是我们之前使用的lowB方法,下面曲线救国nb,就求值和插值这两步是真nb,求值和插值为何是$O(n\lg n)$呢?
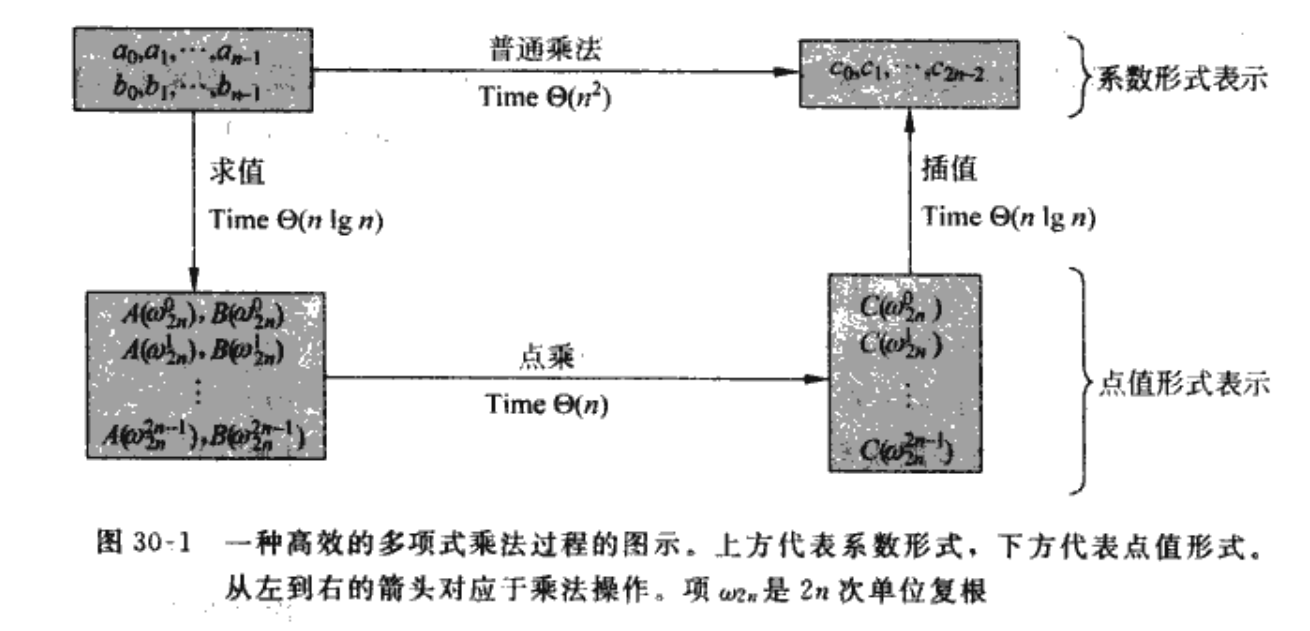
使用之前学过的方法,这两步都是$O(n^2)$的,
求值时需要将$x_0,x_1…$以此带入$A(x)$一共n个自变量,每个自变量求值都是$O(n)$,因此总共$O(n^2)$
插值时需要使用拉格朗日插值法,也是$O(n^2)$
拉格朗日插值公式:
$$
A(x)=\sum_{k=0}^{n-1}y_k\frac{\Pi_{j\neq k }(x-x_j)}{\Pi_{j\neq k}(x_k-x_j)}
$$
其中$(x_0,y_0),(x_1,y_1),…,(x_n-1,y_n-1)$是多项式$A(x)$的点值表示最外层这个求和已经是$O(n)$
用二维数组$M[k][j]=x_k-x_j$预处理分母,
分子预先先直接求出$F(x)=\Pi(x-x_j)$
那么对于一个给定的k,分母就是n个数的积,$O(n)$
分子就是$F(x)/(x-x_j)$,$O(n)$
乘上最外圈的$O(n)$得到$O(n^2)$
也就是说,之前使用的方法是$O(n^2)$的
但是使用快速傅里叶变换这种吊法,就能给他降到$O(n\lg n)$
怎么降的?选点值的时候有讲究
任意n个不同的点就可以确定一个n-1次表达式.
如果选n个单位复根,然后对系数向量$(a_0,a_1,…,a_{n-1})$应用离散傅里叶变换DFT,就可以在$O(n\lg n)$内完成求值,使用逆DFT变换就可以在$O(n\lg n)$完成插值
单位复根儿
“n次单位复根”就是指满足$\omega^n=1$的负数$\omega$,注意是这个$\omega$,不带那个n次方,一定要注意上下角标
欧拉公式
$$
e^{i\pi}+1=0
$$
第k个n次单位复根是$\omega_k=e^{\frac{2\pi ik}{n}}$
显然$\omega_k^n=(e^{\frac{2\pi ik}{n}})^n=e^{2\pi ik}=((e^{i\pi})^2)^k=((-1)^2)^k=1^k=1$
n次单位复根儿恰好有n个,也就是$k=0,1,2,…,n-1$
这n个画在复平面儿上是很整齐的,比如8次复根就长这样:
任何两个相邻的单位复根之间的角度都是固定的,$360/n=360/8$
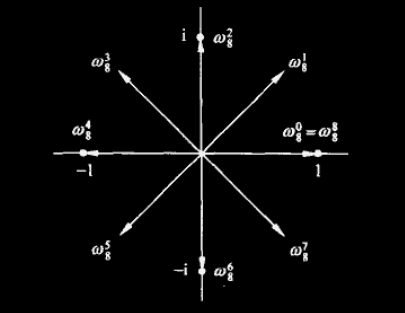
都落在复平面单位元上
显然8次复根只有8个,如果非要写第九个$\omega_8^9$,就和$\omega_8^0$重合了,
然后书上就说这是加法群$(Z_8,+)$,确实是,除了装了个B对于解决问题没有帮助,甚至没有学过抽代的就蒙蔽了
DFT
求n-1次多项式的点值表示时,就需要选取n个点$(x_0,x_1,x,…,x_{n-1})$,然后求出各自的函数值$(y_0,y_1,…,y_{n-1})$
如果选取的n个点是n个富哥儿,那么此时有
$$
y_k=A(\omega_n^k)=\sum_{j=0}^{n-1}a_j\omega n^{jk}
$$
以此得到的$\vec{y}=(y_0,y_1,…,y{n-1})$叫做系数向量$\vec{a}=(a_0,a_1,…,a_{n-1})$的离散傅里叶变换,
记作$\vec{y}=DFT_n(\vec{a})$
笑死,这看上去不就是带入求值吗,选n个富哥有屁用啊?
如果用普通的带入求值,找n个富哥儿和找n个普通人儿没有区别.
富哥儿的作用不能浪费喽,他们和普通值又有啥区别呢?
这就是单位复根儿的几个性质
这几个性质在计算时会体现群论的对称性,这意味着,这n个富哥确实能够比n个普通值携带更多的信息
FFT
fast Fourier transform,快速傅里叶变换
在$O(n\lg n)$内求解DFT的算法
也就是说,DFT并不是一个求解方法,只是娶了n个富哥作为点值表示
仍然可以使用带入求值这种$O(n^2)$的lowB算法求解
而FFT就是一种吊法
他这样变形:
首先n向上取整到最近的2的幂次,这样做是为了保证能够一直二分直到剩1项,反正多取点不会降低精度
后面的n默认就认为是2的幂次了
$$
\begin{aligned}
A(x)&=a_0+a_1x+a_2x^2+…+a_{n-1}x^{n-1}\
&=(a_0+a_2x^2+a_4x^4+…+a_{n-2}x^{n-2})+(a_1x+a_3x^3+a_5x^{5}+…+a_{n-1}x^{n-1})\
&=A^{[0]}(x^2)+xA^{[1]}(x^2)
\end{aligned}
$$
也就是说将$A(x)$按照偶数项和奇数项分开,其中奇数项都提出一个x来,这样子多项式中的x都是偶数,可以提取$x^2$作为自变量,于是得到
$$
\begin{cases}
A^{[0]}(x)=a_0+a_2x+a_4x^2+…+a_{n-2}x^{\frac{n}{2}-1}\
A^{[1]}(x)=a_1+a_3x+a_5x^2+…+a_{n-1}x^{\frac{n}{2}-1}
\end{cases}
$$
时刻不要忘记在求什么,
我们现在已知的是$\vec{a}=(a_0,a_1,a_2,…,a_{n-1})$,$\vec{x}=(\omega_n^0,\omega_n^1,…,\omega_n^{n-1})$
要求的是$\vec {y}=DFT_n(\vec{a})$
现在可以这样算了:
$$
A(x_k)=A(\omega_{n}^k)=A^{[0]}(\omega^{2k}_n)+\omega^k_nA^{[1]}(\omega^{2k}_n)
$$
注意到我们不容易计算$A(x)$是因为,它的项太多了,0次项,1次项等等一直到n-1次项,共n项
而现在对于一个$A^{[0]}(x)$他只有$\frac{n}{2}$项了,工作量直接下降到一半
以此递归,总会有个时候,$A(x)$只有一项,也就是0次项,也就是那个常数项,算也不用算直接返回了,和x没有关系了,和富哥没关系了
写出伪代码:
注意FFT函数的输入是目标多项式的系数向量,不是富哥,因为富哥是作为常数使用的,不需要参数传递
FFT函数输出的是$\vec{y}=DFT(\vec{a})$也就是和将n个富哥直接带入多项式求值得到的n个值相同,但是算法更好
一定注意函数不是y=A(x),而是y=FFT(a)
一定要清楚函数在干什么
1 | vector<int> FFT(vector<int> a){//a是系数,返回y向量 |
这里面有一个y[n/2+i]=y0[i]-pow(omega_n,i)*y1[i],怎么得到的呢?
$$
\begin{aligned}
y[\frac{n}{2}+i]&=A(\omega_n^{\frac{n}{2}+i})\
&=A^{[0]}(\omega_n^{n+2i})+\omega_n^{\frac{n}{2}+i}A^{[1]}(\omega_n^{n+2i})\
&=A^{[0]}(\omega_n^{2i})+\omega_n^{\frac{n}{2}+i}A^{[1]}(\omega_n^{2i})\
&=A^{[0]}(\omega_{\frac{n}{2}}^i)-\omega_n^{i}A^{[1]}(\omega_{\frac{n}{2}}^i)\
&=y_0[i]-\omega_{n}^i y_1[i]
\end{aligned}
$$
这就体现出富哥和普通点的区别了,富哥的变换很灵活
从上面的伪代码可以看出,最底层的递归和自变量无关.
加速发生在这里,将工程量直接缩减到一半
1 | for(int i=0;i<n/2;i++){//一定注意此处上界是n/2 |
每次递归都将工程量缩减一半,因此总工程量直接对n取对数
$$
T(n)=2T(\frac{n}{2})+\Theta(n)=\Theta(n\lg n)
$$
好了到此FFT的思路有了,求值结束,也就是我们求得了$y=DFT(a)$
举个例子,$A(x)=1+2x+x^2+x^3$,正好有$2^2=4$项,n=4
4次单位复根$\omega_4^k=e^{\frac{2\pi ik}{4}}$
2
3
4
5
6
7
8
9
10
11
12
13
14
n=<1,2,1,1>.length()=4;
a0=<1,1>;
a1=<2,1>;
w1;
y0=FFT(<1,1>){
n=<1,1>.length()=2;
a0=<1>;
a1=<1>;
y0=FFT(<1>)=<1>;
y1=FFT(<1>)=<1>;
y[0]=y[0]+w1
}
}
下面考虑如何从点值形式倒回去,也就是如何在$O(n\lg n)$实现插值
现在已知的是$\vec{y}$和$\vec{x}={\omega_{n}^0,\omega_n^1,…,\omega_n^{n-1}}$,求系数向量$\vec{a}$
显然可以待定系数法设n个系数,然后带入自变量和因变量,解一元n次方程组.
高斯消元法是$O(n^2)$的lowB算法,要用吊算法
写成矩阵形式

也就是说,一眼顶针,鉴定为范德蒙矩阵,必然可逆且逆矩阵唯一
现在要用尽可能快的方法求解这个范德蒙矩阵$V$的逆矩阵,这个求解方法就是算法关键
这有个定理$V^{-1}_n[j,k]=\frac{\omega_n^{-kj}}{n}$
怎么得出来的,我线性代数忘了,不会解,但是$VV^{-1}$算一下确实得到$E$,满足互逆矩阵的定义
由于$\vec{a}=\vec V^{-1}\vec{y}$
$a_j$就等于$\vec V^{-1}$的第j行与$\vec y$的乘积,也就是说
$$
a_j=\sum_{k=0}^{n-1}V_n^{-1}[j,k]\times y_k\
=\sum_{k=0}^{n-1}\frac{\omega^{-kj}n}{n}\times y_k\
=\frac{1}{n}\sum{k=0}^{n-1}\omega_n^{-kj}\times y_k
$$
求解一个$a_j$,是$O(n)$复杂度的,
共有n个$a_j$,总共就是$O(n^2)$复杂度的,怎么降到$O(n\lg n)$呢?
回忆正向的FFT是干啥的来着
是求解$\vec{y}=DFT_n(\vec {a})$问题的
其中$y_j=\sum_{k=0}^{n-1}a_j\omega_n^{jk}$
类比一下
$$
\begin{aligned}
n a_j&=\sum_{k=0}^{n-1} y_k\omega_n^{-jk}\
y_j&=\sum_{k=0}^{n-1}a_k\omega_n^{jk}
\end{aligned}
$$
令$\vec{y’}=n\vec{a},$
$\vec{a’}=\vec{y}$
令单位富哥变成单位负哥,就可以直接带入FFT函数求解了$\vec{y’}$了
解出来都除以n就得到了$\vec{a}$
因此又在$O(n\lg n)$内解决了
回到多项式求积
卷积定理:
对于两个长度为n的向量$\vec a,\vec b$
$$
a\otimes b=DFT^{-1}{2n}(DFT{2n}(a)·DFT_{2n}(b))
$$
将多项式A,B只保留系数看成向量a,b,此时$a\otimes b$就是积多项式AB的系数向量
