dustland

dustball in dustland

动态规划-状压DP

Posted on Edited on

动态规划-状压DP

状态压缩DP,也就是把局面状态压缩到一个整数中,用整数的运算表示状态转移

模板题一般是,往棋盘上放同一种棋子,并且不能让他们掐架,问题有两种:

一共要放k个,求放法有几种?

最多放多少个?

g++ -std=c++11 -O2

P1896 八王八

一个\(N\times N\)的国象棋盘上放\(k\)个王八,要求这k个王八不能掐架.求有多少种放王八的方法

其中\(1\leq N\leq 9,0\leq k\leq N\times N\)

类似于八皇后问题,但是王八的攻击范围只有周围八格,更近

状态压缩

棋盘的每个格子,要么有王八,要么没王八,因此 可以用1表示有,0表示无的状态

那么整个棋盘可以看成有N行,每行有N个格子

比如一个\(4\times 4\),没有王的棋盘就可以是

1
2
3
4
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0

可以将一行压缩为一个整数,最左侧是最低位比如

1 0 0 1 0 1 0 ->0101001b=41

如果想让一行中的王八不掐架,那么不能有任何两个1相邻.这一点怎么判断呢?

假设current_state=41表示当前行状态

那么(current_state&((current_state>>1)|current_state<<1))就可以判断有没有王八掐架

为啥呢?

比如状态41显然是合法的

状态 整数 二进制
current_state 41 0101001
current_state<<1 1010010
current_state>>1 0010100
(current_state<<1)|(current_state>>1) 1010110
current_state 0101001
(current_state&((current_state>>1)|(current_state<<1)) 0000000

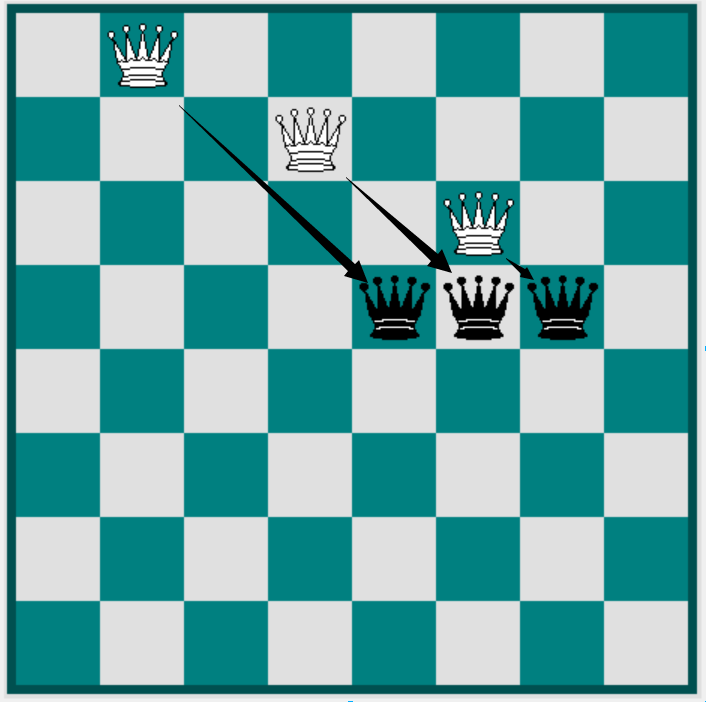
如何让相邻两行的王八不掐架呢?

(current_state&((previous_state)|(previous_state<<1)|(previous_state>>1)))

道理类似于不让一行中的王八掐架,上一行的一个王八,那么本行中该王八的左下,正下,右下都不能有王八

状态转移

设计状态:

dp[currnet_row][cnt_king_used][current_state]表示:

已经安排了[1,current_row]的王八,

已经安排了cnt_king_used个王八,

当前行,也就是第current_row的状态是current_state

状态转移方程: \[ \begin{aligned} &dp[current\_row][cnt\_king\_used][current\_state]=\\ &\sum_{previous\_state}dp[previous\_row][cnt\_kings\_used-cnt\_kings\_of[current\_row]\ ][previous\_state] \end{aligned} \] 初始状态:

前0行(不存在这一行),放了0个王八,状态显然是0,此时的摆放方法dp[0][0][0]=0

完整程序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

long long dp[10][100][2000];//dp[i][j][k]前i行中已经摆了j个王,其中第i行的状态是k.的数量
int n,k;

vector<int>legal_states;
int cnt_kings_in_state[2000];

bool isLegalState(const int &k){
    if((k&((k<<1)|(k>>1)))==0){
        return true;
    }
    return false;
}
bool isInvasion(const int &a,const int &b){
    return (a&((b<<1)|(b>>1)|b));
}

int main(){
    cin>>n>>k;
    int current_state;
    int cnt_state;
    for(int i=0;i<(1<<n);i++){
        current_state=i;
        cnt_state=0;
        while(current_state){
            cnt_state+=current_state&1;
            current_state>>=1;
        }
        cnt_kings_in_state[i]=cnt_state;
        if(isLegalState(i)){
            legal_states.push_back(i);
        }
    }
    dp[0][0][0]=1;
    for(int current_row=1;current_row<=n;current_row++){
        
        auto previous_row=current_row-1;

        for(auto current_state:legal_states){//当前行合法状态
            
            for(auto previous_state:legal_states){//上一行的合法状态

                if(isInvasion(current_state,previous_state)==false){

                    for(
                        int cnt_tot_kings=cnt_kings_in_state[current_state];
                        cnt_tot_kings<=k;
                        ++cnt_tot_kings
                    ){
                        
                        dp[current_row][cnt_tot_kings][current_state]+=
                            dp[previous_row][cnt_tot_kings-cnt_kings_in_state[current_state]][previous_state];

                    }
                }
            }
        }
    }
    long long result=0;
    for(auto current_state:legal_states){
        result+=dp[n][k][current_state];
    }
    cout<<result<<endl;

    return 0;
}

P1219 八皇后

\(N\times N\)的棋盘上要放N的皇后,要求N个皇后不能掐架,求多少种放皇后的方法

\(6\leq N\leq 13\)

状态压缩

N行,每行N位,每位0表示没有皇后,1表示有皇后

一个int有32位,足够表示一行

每行的最左侧格子是int的最低位

状态转移

设计状态

\(dfs(col\_state,diagonal\_state,rdiagonal\_state,row)\)

表示当前要放第row行的皇后,

之前所有的皇后控制的所有列存放在col_state中,

之前所有皇后控制的左上到右下的斜线在本行的影响存放在diagonal_state中

之前所有皇后控制的右上到左下的斜线在本行的影响存放在人diagonal_state中

显然\(dfs(col\_state,diagonal\_state,rdiagonal\_state,row)\)的任务就是,结合前三个参数,在本行找一个安全位置放一个皇后,然后进入下一层dfs

啥意思呢?8

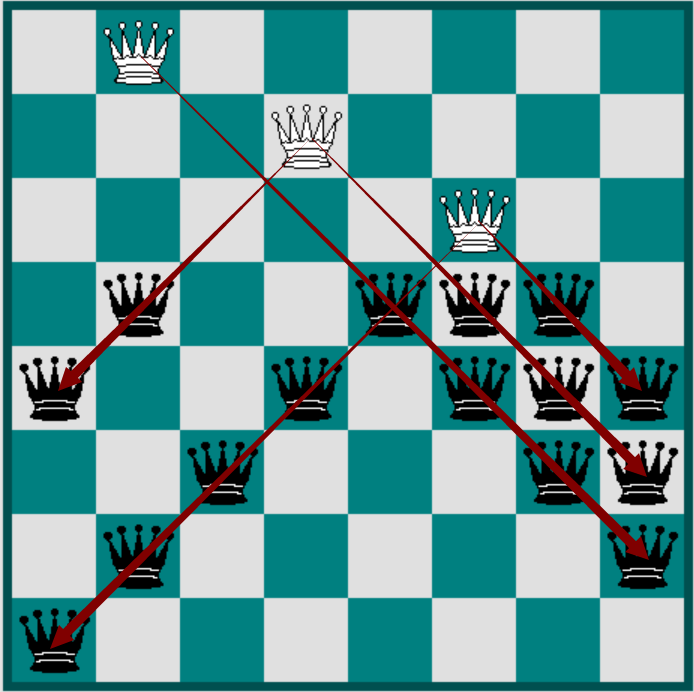
假如现在要放第四行,前三行的皇后如图所示

image-20221222114520664

这三个皇后控制的列对第四行的影响如图

image-20221222114303317

那么此时第四行的2,4,6列就不允许放皇后,

此时col_state=00101010b,(最左侧格子在最低位)表示第2,4,6列不允许使用

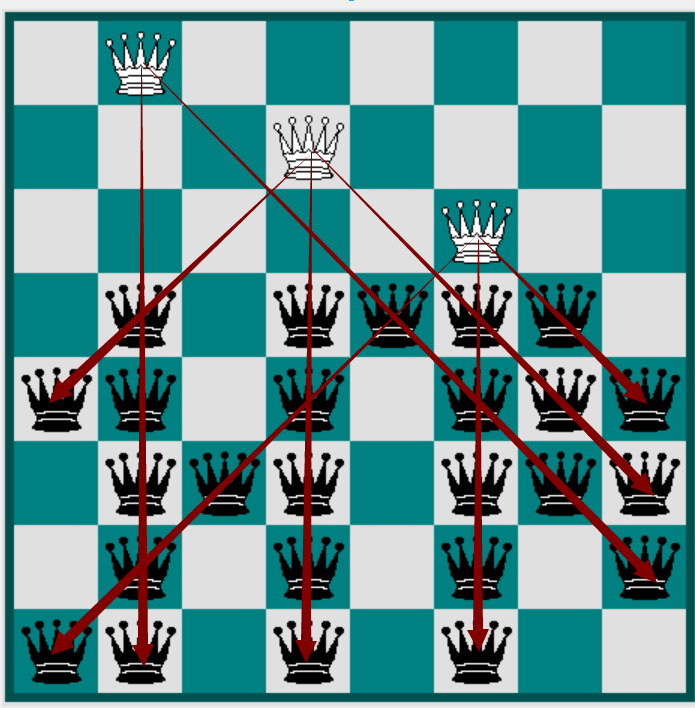
前三个皇后在左上到右下的斜线上,对第四行产生的影响如图

image-20221222114701433

即此时diagonal_state=01110000(最左侧格子在最低位),表示第5,6,7列不允许使用

rdiagonal_state同理

下面考虑这三个表示占用状态的参数如何维护

显然col_state最容易维护,只要第i列上有过皇后,col_state的相应二进制位就置1

对于diagonal_state,假设本行的皇后放在第i列,那么他会影响下一行的i+1列,因此从当前行的dfs进入下一行的dfs时,只需要把diagonal_state加上本行的皇后列位置,然后右移1位传递给下层dfs

image-20221222150322875

综上,对于当前行的dfs,放置皇后时需要考虑的因素如图:

image-20221222150632385

状态转移方程采用"推"的方式,从row层推进到row+1层 \[ \begin{aligned} &dfs(col\_state,diagonal\_state,rdiagonal\_state,row)\\ \Rightarrow &dfs(col\_state|current\_state,(diagonal\_state|current\_state)>>1,(rdiagonal\_state|current\_state)<<1,row+1) \end{aligned} \]

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int n;
const int maxn=20;
int log_2[10000];
int cnt_success=0;
int limit_state;
int col[maxn];//第i行放在第col[i]列上
int lowbit(int &x){
    return x&(-x);//-x为取补,~x为按位取反
}
void print(){
    for(int i=1;i<=n;++i){
        cout<<col[i]+1<<" ";
    }
    cout<<endl;
}
void dfs(int column_state,int diagonal_state,int rdiagonal_state,int row){
    if(row>n){
        ++cnt_success;
        if(cnt_success<=3){//打印前三个排列
            print();
        }
        return;
    }
    int capture_state=(column_state|diagonal_state|rdiagonal_state)&limit_state;
    int available_state=(~capture_state)&limit_state;//~按位取反,
    int position_state;
    int position;
    while(available_state){
        position_state=lowbit(available_state);//lowbit每次先尝试最低位,保证了得到结果的顺序是按照字典序的
        position=log_2[position_state];
        col[row]=position;
        dfs(column_state|position_state,(diagonal_state|position_state)>>1,(rdiagonal_state|position_state)<<1,row+1);
        available_state-=position_state;
    }
}

int main(){
    cin>>n;
    limit_state=(1<<n)-1;//规定yi'man
    log_2[1]=0;
    for(int i=2;i<10000;i++){//初始化log_2对数函数
        log_2[i]=log_2[i/2]+1;
    }
    dfs(0,0,0,1);
    cout<<cnt_success<<endl;
    return 0;
}

P1879 八将军

\(M\times N\)个格子的矩形地面

然后输入\(M\times N\)个数表明这个地面是否肥沃,1肥沃,0贫瘠

其中\(1\leq M,N\leq 12\)

肥沃的土地可以种草,贫瘠的不行

任何两个草地不能有相邻边,可以有相邻顶角

求有多少种安排方法

问题可以向八王八靠拢,如果种草地可以视为占了一个中国象棋的将军,前后左右四个格子内不允许有第二个将军.贫瘠的格子不允许放棋

如果八王八问题中也有一些棋盘不允许放置棋子则和本题就很相似了

状态压缩

一行最多有12个格子,每个格子要么种草,要么不中,一个二进制位两种状态表示一个格子即可,那么一行只需要12个二进制位,显然一个int有32位足够表示一行的状态

贫瘠的格子如何建模?贫瘠的格子不允许种草就行了呗

状态转移

类比八国王问题,设计dp状态 \[ dp[current\_row][current\_state] \] 表示:

已经安排了[1,current_row]行,

其中第current_row行的状态是current_stata,

满足上述两个条件的不同安排数目是dp[current_row][current_state]

状态转移方程是 \[ dp[current\_row][current\_state]=\\ \sum_{previous\_state}dp[previous\_row][previous\_state] \] 这里要求previous_state和current_state两个状态不能相互冲突,也就是上一行的种草格子,下一行这个格子不允许种草

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <iostream>
#include <vector>
#include <iomanip>
#include <algorithm>
using namespace std;
int m,n;
const int maxn=14;
const int mod=1e9;
int row_base_state[maxn];//输入一行土地贫瘠状态之后压缩成一个整数,row_base_state[i]表示第i行的地皮是贫瘠还是肥沃
vector<int> row_legal_state[maxn];//ro_legal_state[i]表示第i行的所有合法状态集合(同行内没有相邻草地并且考虑贫瘠土地)
int row_limit_state;//行状态上限
int dp[maxn][1000000];//dp[current_row][current_state],第1到current_row行都已经安排,其中第current_row行的状态是current_state


int main(){
    cin>>m>>n;//m行,每行有n列
    row_limit_state=(1<<n)-1;//行状态上限
    int single_state;//用于承载一个格子的状态
    for(int i=1;i<=m;i++){//获取输入压缩到row_base_state
        int row_state=0;//用于压缩一行的状态
        for(int j=1;j<=n;j++){
            cin>>single_state;
            //最先输入的格子权位最高,也就是说最左侧的格子在状态的最高二进制位
            row_state=row_state*2+single_state;//行状态=刚才的行状态左移一位加上新格子的状态
        }
        row_base_state[i]=row_state;//计算得出了第i行的压缩状态
        for(row_state=0;row_state<=row_limit_state;++row_state){//计算第i行的所有合法种草状态,第i行的每种合法种草状态都放到row_legal_state[i]中
            if((row_state&((row_state<<1)|(row_state>>1)))==0 && ((row_state&((~row_base_state[i])&row_limit_state))==0)){
                row_legal_state[i].push_back(row_state);
            }
            
        }
    }
    dp[0][0]=1;//设置dp初始条件,啥也不种的状态只有一种
    row_legal_state[0].push_back(0);//第0行没有任何合法状态
    for(auto current_row=1;current_row<=m;++current_row){//
        auto previous_row=current_row-1;
        for(auto current_row_state:row_legal_state[current_row]){
            for(auto previous_row_state:row_legal_state[previous_row]){
                if((current_row_state&previous_row_state)==0){//两行不能冲突
                    dp[current_row][current_row_state]+=dp[previous_row][previous_row_state];//状态转移
                    
                }
            }
        }
    }   
    int result=0;
    for(int i=0;i<=row_limit_state;i++){
        result=(result+dp[m][i])%mod;//第m行的所有状态都要考虑在内
    }
    cout<<result<<endl;
    return 0;
}

P2704 八炮兵

给一个P和H表示的地形地图

img

其中只有P(Plain,平原)格子可以放炮兵,H山地不行

状态压缩

一个炮兵的打炮范围是横竖的两格相当于中象里将军腿再长一点

实际上和P1879棒子地很相似了,P1879种草的方格相当于放了有一个中象的将军,这个题的格子相当于放了一个壮一点的将军

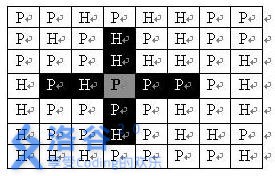
原来一个将军顶多影响跟前的四个格子,现在一个炮可以影响8个格子,

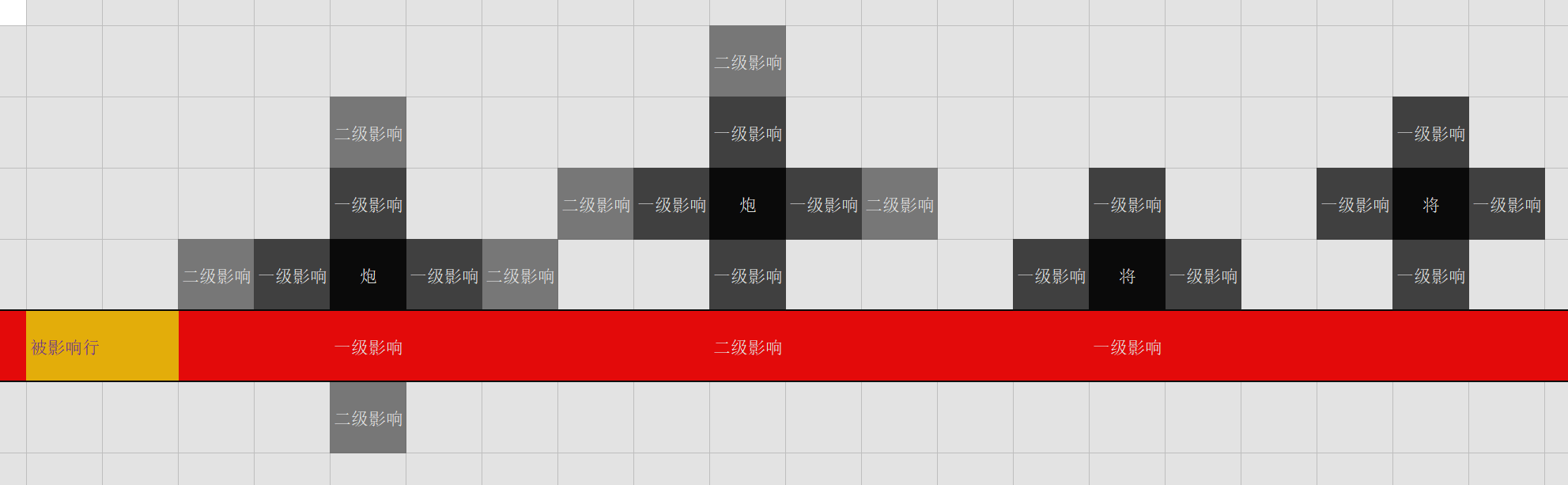
不妨把跟前这四个格子叫做"一级影响",稍微远一点的四个格子叫做"二级影响",如下图示意

image-20221222194252888

可见一个将军和一个炮的区别就是,将军只有一级影响,炮还有二级影响

P1879这个题中要安排一行时,只需要考虑上一行给这一行造成的一级影响.

本题中除了一级影响,还要考虑二级影响,因此本题可以看作P1879的推广,

状态转移

原来的状态dp[current_row][current_state]表示1到current_row行已经安排完毕,其中current_state是第current_row行的状态,也就是对current_row+1行的"一级影响"

因此拓展到有二级影响的情况,应该这样设置状态dp[current_row][current_state][previous_state],意思是

当前已经安排好了1到current_row行,

第current_row行的状态是current_state,

第previous_row=current_row-1行的状态是previous_state

dp[current_row][current_state][previous_state]等于在前述三个条件下得到的最大炮兵数量 \[ 当前状态的最大炮兵数=max(枚举与当前行不冲突的上一行状态的最大炮兵数+当前行状态贡献的炮兵数) \]

状态转移方程就是:

1
2
3
dp[current_row][current_state][previous_state]=max(
	dp[previous_row][previous_state][preprevious_state]+cnt_of_cannons_in_state[current_state];
)

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int maxn=110;//最大行数
int n,m;//n行,m列
int row_limit_state;//一行的最大状态
int row_base_state[maxn];//一行中的地形状态,row_base_state[i]为第i行的地形状态
vector<int> row_legal_states[maxn];//只看一行时,该行的所有合法摆放炮兵的状态集合,row_legal_states[i]为第i行所有可以摆放的状态
int cnt_max_cannons;//记录最大炮兵数量
int dp[maxn][1025][1025];
int cnt_cannons_in_state[1025];//cnt_cannons_in_state[state]表示当一行的炮兵状态为state时,放了几个炮兵


int main(){
    cin>>n>>m;//n行m列
    // if(n)
    int single_state;//输入char类型的地形转换成0或者1表示的地形

    char terrain;//存放地形输入

    row_limit_state=(1<<m)-1;

    for(auto row_state=0;row_state<=row_limit_state;++row_state){//预处理cnt_cannons_in_state数组
        int row_temp_state=row_state;
        int cnt_cannons=0;
        while(row_temp_state){
            cnt_cannons+=row_temp_state&1;//不停右移直到降为0,只关心最低为有没有1
            row_temp_state>>=1;
        }
        cnt_cannons_in_state[row_state]=cnt_cannons;
    }


    for(int row=1;row<=n;row++){
        int row_state=0;
        for(int col=1;col<=m;++col){
            cin>>terrain;
            if(terrain=='P'){
                single_state=1;
            }
            else{
                single_state=0;
            }
            row_state=row_state*2+single_state;
        }
        row_base_state[row]=row_state;//保存地形状态

        //立刻计算基于当前行的地形状态,可以得出的所有合法的炮兵摆放状态
        for(row_state=0;row_state<=row_limit_state;row_state++){
            if(
                (row_state&(((row_state<<1)|(row_state<<2)|(row_state>>1)|(row_state>>2) )&row_limit_state)   )==0//这个炮兵的摆放状态不能自相冲突
                &&
                (row_state&((~row_base_state[row])&row_limit_state))==0//这个炮兵的摆放状态要满足地形要求
            ){
                row_legal_states[row].push_back(row_state);
                // cout<<row_state<<endl;
            }
        }
    }


    dp[0][0][0]=1;
    row_legal_states[0].push_back(0);//一定要这个初始化,第二行会查第0行的合法状态


    for(auto current_state:row_legal_states[1]){//第一行需要特殊处理,因为第一行往前看两行不存在第-1行,不能作为数组下标
        dp[1][current_state][0]=cnt_cannons_in_state[current_state];
        cnt_max_cannons=max(cnt_max_cannons,dp[1][current_state][0]);//一定不要忘记统计只有一行时的最大炮兵数量,测试点11专门卡这个
    }

    for(auto current_row=2;current_row<=n;++current_row){//第二行往前看两行正好是第0行,下标访问正常
        auto previous_row=current_row-1;//上一行行号
        auto preprevious_row=previous_row-1;//上两行行号
        for(auto current_state:row_legal_states[current_row]){//枚举当前行合法状态
            for(auto previous_state:row_legal_states[previous_row]){//枚举上一行合法状态
                for(auto preprevious_state:row_legal_states[preprevious_row]){//枚举上两行合法状态
                    if(
                        (previous_state & preprevious_state)==0//前两行的炮兵不能打架
                        &&
                        (current_state&(previous_state|preprevious_state))==0//本行和前两行的炮兵不能打架
                    ){
                        dp[current_row][current_state][previous_state]=max(//状态转移方程
                            dp[current_row][current_state][previous_state],
                            dp[previous_row][previous_state][preprevious_state]+cnt_cannons_in_state[current_state]
                        );
                        cnt_max_cannons=max(cnt_max_cannons,dp[current_row][current_state][previous_state]);
                    }
                }
            }
        }
    }
    // for(auto current_state:row_legal_states[n]){
    //     cnt_max_cannons=max(cnt_max_cannons,dp[n])
    // }
    cout<<cnt_max_cannons<<endl;
    return 0;
}

P2051 八中象炮

在一个\(n\times m\)的棋盘上,任意放中象的炮,要求任意两个炮不能相互攻击,随便放炮,问最多有多少种放法

啥时候能炮打炮?一条水平或者竖直线上有仨个以上的炮就要打炮了

因此就问题转化为,\(n\times m\)个方格,每行每列可以有0或者1或者2个石头,求有多少种摆放方法

状态压缩

我最初的想法是,每行,每列都记录已经放过几个石头,然后直接深搜

dfs(x,y)是当前要在第x行第y列放石头,首先判断能否放石头,如果能则尝试放上石头然后下一步深搜.

不管能不能放石头,都要有一个直接下一步深搜

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int maxn=110;
const int mod=9999973;
int n,m;
int cnt_on_col[maxn];
int cnt_on_row[maxn];
int cnt_result=0;
void DFS(int y,int x){//第y行,第x列
    if(y<=n&&x>m){
        DFS(y+1,1);
        return;
    }
    if(y>n){
        cnt_result=(cnt_result+1)%mod;
        return;
    }
    if(cnt_on_col[x]<2&&cnt_on_row[y]<2){
        ++cnt_on_col[x];
        ++cnt_on_row[y];
        DFS(y,x+1);
        --cnt_on_col[x];
        --cnt_on_row[y];
    }
    DFS(y,x+1);

}
int main(){
    cin>>n>>m;
    DFS(1,1);
    cout<<cnt_result<<endl;

    return 0;
}

结果就三个测试点过了,其他全都TLE

狗屁状压,dp[i][j][k]表示前i行中的列,有一个炮的列有j个,有两个炮的列有k个

完事