dustland

dustball in dustland

动态规划-区间DP

Posted on Edited on

动态规划-区间DP

模板题一般长这样:

给一个区间[1,n]

给定一种操作:合并子区间,两个相邻子区间[i,j],[j+1,k]合并,得到一定的收益或者付出一些代价.这个收益或者代价必然是和两个子区间相关的函数,比如sum[i,j]+sum[j+1,k]

求将整个区间合并为一个数,获得的最大收益或者付出的最小代价

P1880 合并环状石子

一圈石子有n组,其中第i组有a[i]个,合并两组石子的代价是两组石子个数和,求将所有石子合并成一组需要的最大代价和最小代价

本题需要先把环拆成线,其弱化版也就是无环版本P1775 石子合并（弱化版

首先需要把这个圈解开,比较好的方法是将[1,n]展开成线性,然后复制一遍接到后面,就是

总下标 1 2 3 ... n-1 n n+1 n+2 n+3 ... 2n-1 2n
原下标 1 2 3 ... n-1 n 1 2 3 ... n-1 n
石子个数 a[1] a[2] a[3] .. a[n-1] a[n] a[1] a[2] a[3] ... a[n-1] a[n]

设计状态

\[ max\_dp[i][j]=将[i,j]区间合并成一组的最大代价\\ min\_dp[i][j]=将[i,j]区间合并 成一组的最小代价 \]

显然边界条件是: \[ \forall _{1\le i\le 2n}max\_dp[i][i]=0\\ \forall _{1\le i\le 2n}min\_dp[i][i]=0\\ \] 意思是将一组石子和自己合并(合并个寂寞),其代价为0,因为不需要合并

\[ max\_dp[i][j]=\max_{i\leq k<j}(max\_dp[i][k]+max\_dp[k+1][j])+\sum_{i\leq l\leq j}a[l]\\ min\_dp[i][j]=\max_{i\leq k<j}(min\_dp[i][k]+min\_dp[k+1][j])+\sum_{i\leq l\leq j}a[l] \]

其中\(\sum_{i\leq l\leq j}a[l]\)也就是从i到j的石子总个数,可以维护前缀和降低复杂度 \[ \sum_{i\leq l\leq j}a[l]=prefix[j]-prefix[i-1] \]

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include <iostream>
#include <algorithm>
using namespace std;
int n;
const int INF=1e9;
const int maxn=210;
int value[maxn];
int max_dp[maxn][maxn];//max_dp[i][j]为合并闭区间[i,j]所需要的最大代价
int min_dp[maxn][maxn];
int prefix[maxn];
int main(){
    cin>>n;
    
    int v;
    prefix[0]=0;
    for(int i=1;i<=n;i++){
        cin>>v;
        value[i]=value[i+n]=v;
        prefix[i]=prefix[i-1]+value[i];
        max_dp[i][i]=max_dp[i+n][i+n]=0;//初始化边界条件,只有一堆时不需要合并,因此无代价
        min_dp[i][i]=min_dp[i+n][i+n]=0;
    }
    for(int i=1+n;i<=n*2;i++){
        prefix[i]=prefix[i-1]+value[i];
    }

    for(auto delta=1;delta<n;delta++){//delta,步长,确定区间左端点i之后,右端点j=i+delta,显然delta初始值应该是1
        for(auto i=1;i+delta<=2*n;i++){
            auto j=i+delta;
            auto temp_max=0;
            auto temp_min=INF;//临时变量,用于计算最值
            for(auto k=i;k<j;++k){
                temp_max=max(temp_max,max_dp[i][k]+max_dp[k+1][j]+prefix[j]-prefix[i-1]);//状态转移
                temp_min=min(temp_min,min_dp[i][k]+min_dp[k+1][j]+prefix[j]-prefix[i-1]);
            }
            max_dp[i][j]=temp_max;
            min_dp[i][j]=temp_min;
        }
    }
    int max_value=0;
    int min_value=1e9;
    for(int i=1;i<=n;i++){
        max_value=max(max_value,max_dp[i][i+n-1]);
        min_value=min(min_value,min_dp[i][i+n-1]);
    }
    cout<<min_value<<endl<<max_value<<endl;


    return 0;
}

P1063 合并能量珠子

每个珠子有两头,记作(l,r),相邻两个珠子的相向两头数值相同,比如 \[ (a,b)(b,c)(c,d)(d,a) \] 合并两个相邻珠子\((a,b)(b,c)\)得到的能量是\(a\times b\times c\),合并之后形成新珠子\((a,c)\)

将整个项链合并,求得到的最大能量值

还是将整个环拆成[1,n]然后拷贝一份接到后面

\(dp[i][j]\)表示合并区间[i,j]能够得到的最大能量,其中i表示第i个珠子,j表示第j个珠子

边界条件仍然是\(dp[i][i]=0\),只有一个珠子不需要合并

状态转移: \[ dp[i][j]=\max_{i\le k< j}(dp[i][k]+dp[k+1][j]+node[k].l\times node[k].r\times node[k+1].r) \]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
#include <iostream>
#include <algorithm>
#include <vector>
#include <string>
using namespace std;
const int maxn=210;
int n;
struct Bead{
    int __energy;//合并成当前珠子时能够获得的最大能量
    int __l;//左标记
    int __r;//右标记
    Bead(int _l=0,int _r=0,int _e=0):__l(_l),__r(_r),__energy(_e){}
    int l()const{
        return __l;
    }
    int r()const{
        return __r;
    }
    void setL(int _l){
        __l=_l;
    }
    void setR(int _r){
        __r=_r;
    }  
    void setEnergy(int _e){
        __energy=_e;
    }
    int energy(){
        return __energy;
    }
    string toString()const{
        return "("+to_string(__l)+","+to_string(__r)+")";
    }
    friend ostream &operator<<(ostream &os,const Bead &bead){
        os<<bead.toString();
        return os;
    }
}bead[maxn][maxn];
int dp[maxn][maxn];


int main(){
    cin>>n;
    int l;
    int r;
    for(int i=1;i<=n;i++){
        cin>>l;
        bead[i][i].setL(l);
        bead[i+n][i+n].setL(l);
        bead[i+n-1][i+n-1].setR(l);
        bead[i-1][i-1].setR(l);
    }
    bead[2*n][2*n].setR(bead[0][0].r());
    for(auto delta=1;delta<n;++delta){
        for(auto i=1;i+delta<=2*n;++i){
            auto j=i+delta;
            int max_energy=0;
            int temp_energy=0;
            int max_k=0;
            for(auto k=i;k<j;++k){
                
                temp_energy=max(max_energy,bead[i][k].energy()+bead[k+1][j].energy()+bead[i][k].l() * bead[i][k].r() * bead[k+1][j].r());
                if(temp_energy>max_energy){
                    max_energy=temp_energy;
                    max_k=k;
                }
            }
            bead[i][j].setEnergy(max_energy);
            bead[i][j].setL(bead[i][max_k].l());
            bead[i][j].setR(bead[max_k+1][j].r());
        }
    }
    int result=0;

    for(int i=1;i<=n;i++){
        int j=i+n-1;
        result=max(result,bead[i][j].energy());
    }
    cout<<result<<endl;
    return 0;
}

P1005 矩阵取数

对于一个给定的 \(n \times m\) 的矩阵，矩阵中的每个元素 \(a_{i,j}\) 均为非负整数。游戏规则如下：

  1. 每次取数时须从每行各取走一个元素，共 \(n\) 个。经过 \(m\) 次后取完矩阵内所有元素；
  2. 每次取走的各个元素只能是该元素所在行的行首或行尾；
  3. 每次取数都有一个得分值，为每行取数的得分之和，每行取数的得分 = 被取走的元素值 \(\times 2^i\)，其中 \(i\) 表示第 \(i\) 次取数（从 \(1\) 开始编号）；
  4. 游戏结束总得分为 \(m\) 次取数得分之和。

对于任意矩阵，可以求出取数后的最大得分。

由于第i次取数的权重为\(2^i\),显然应尽量保留大数放到最后取

并且取第一行和第二行的数没有影响

因此实际上可以先解决一行内的取数问题,问题转化为:

m个数,第i个数是a[i],每次取数只能从头或者尾取数,第j次取数x的得分是\(2^j\times x\),求m次取数最高得分

如果没有只能头尾取数的限制,显然直接m个数排序后按照从小到达的顺序取数,现在有一个只能从头或者尾取数的限制

暴力搜索的算法容易想到dfs(deque,level)表示当前双端队列deque,当前要取第level个数

但是m最大为80,这就意味着dfs的时间复杂度是\(O(2^{80})\)显然超时

显然要使用更吊的方法

设计状态: \[ dp[i][j]\leftarrow要在闭区间[i,j]中取数,全部取完后最终能够得到的最大值 \]

状态转移: \[ dp[i][j]=max(dp[i][j-1]+a[j][j]\times 2^k,dp[i+1][j]+a[i][i]\times 2^k) \] 其中k是第k次取数,k=n-i-j+2

dp[1][n]是第1次取数

屑题害得考尼玛的高精度,有个🔨意思啊,没活可以咬打火机

P4767 邮局

v个村庄,p个邮局

第i个村庄在a[i]位置

邮局都要建在村庄里,要求所有村庄到最近邮局的距离和最小

求这个最小距离和是多少

设计状态: \[ dp[i][j]表示前i个村庄放了j个邮局,最小距离和 \]

状态转移 \[ dp[i][j]=\min_{1\le k\le i}(dp[k][j-1]+w(k+1,i)) \] 其中\(w(l,r)\)表示,在第l个和第r个(包括两头)村庄之间放一个邮局时,这一段上的村庄的最短距离和

这个玩意儿怎么求呢?

设\([l,r]\)区间上的村庄坐标为\(x[l],x[l+1],x[l+2],...,x[r-1],x[r]\)

假设放这个邮局的坐标为\(x\),则问题相当于 \[ w(l,r)=min(|x-x[l]|+|x-x[l+1]|+|x-x[l+2]|+...+|x-x[r-1]|+|x-x[r]|) \] 令\(f(x)=|x-x[l]|+|x-x[l+1]|+|x-x[l+2]|+...+|x-x[r-1]|+|x-x[r]|\)

也就是求该函数在\([l,r]\)上的最小值点

怎么求呢?画图观察一下,

如果有奇数项,比如\(y=|x-x_1|+|x-x_2|+|x-x_3|\),这个函数必然有一个尖儿,也就是我们需要的最小值,并且这个极小值点等于 \(中位数(x_1,x_2,x_3)\)

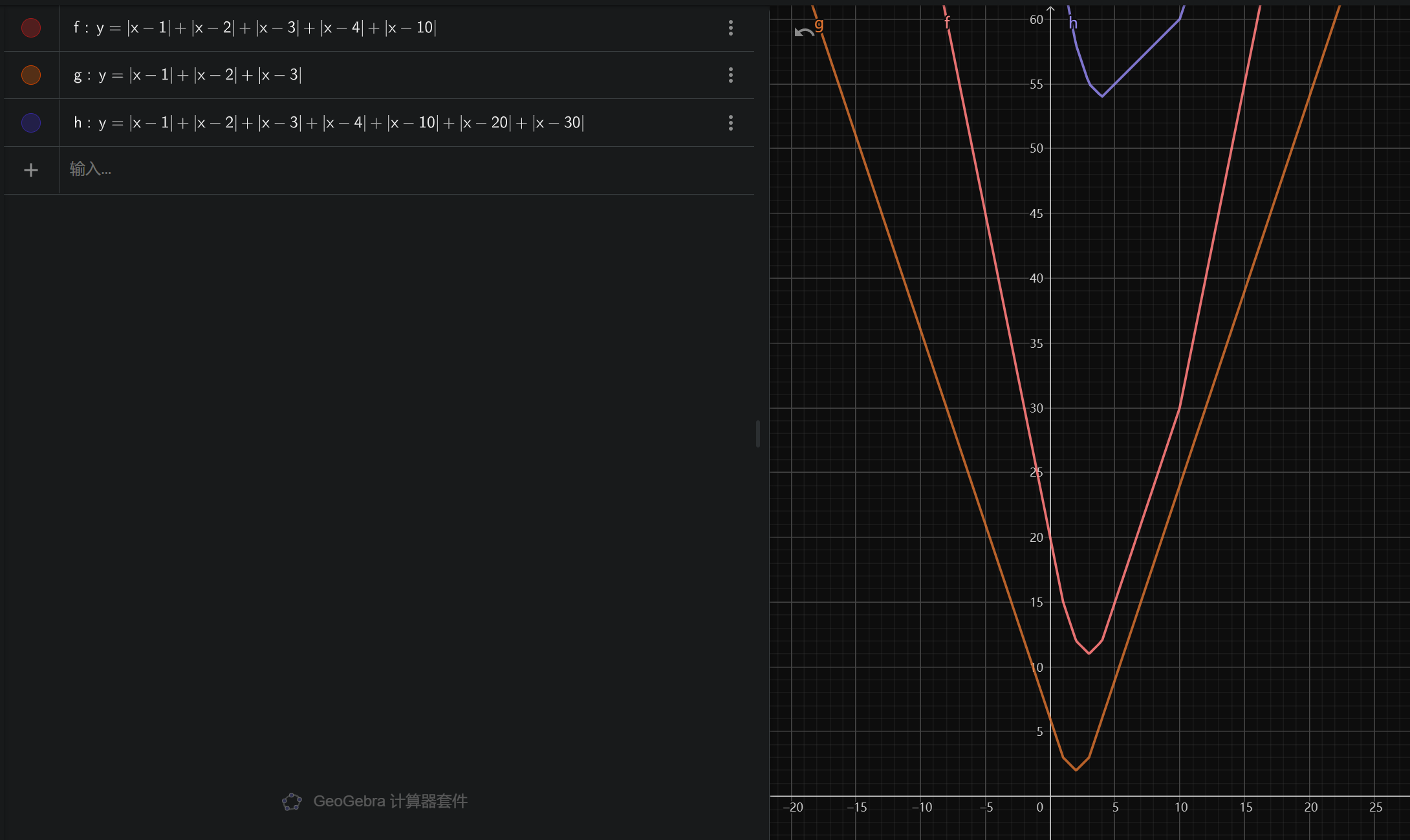
image-20221223163332854

如果有偶数项,比如\(y=|x-x_1|+|x-x_2|+|x-x_3|+|x-x_4|\),就没有这个尖儿,但是有一个水平的最低谷,这个最低谷介于两个中位数之间

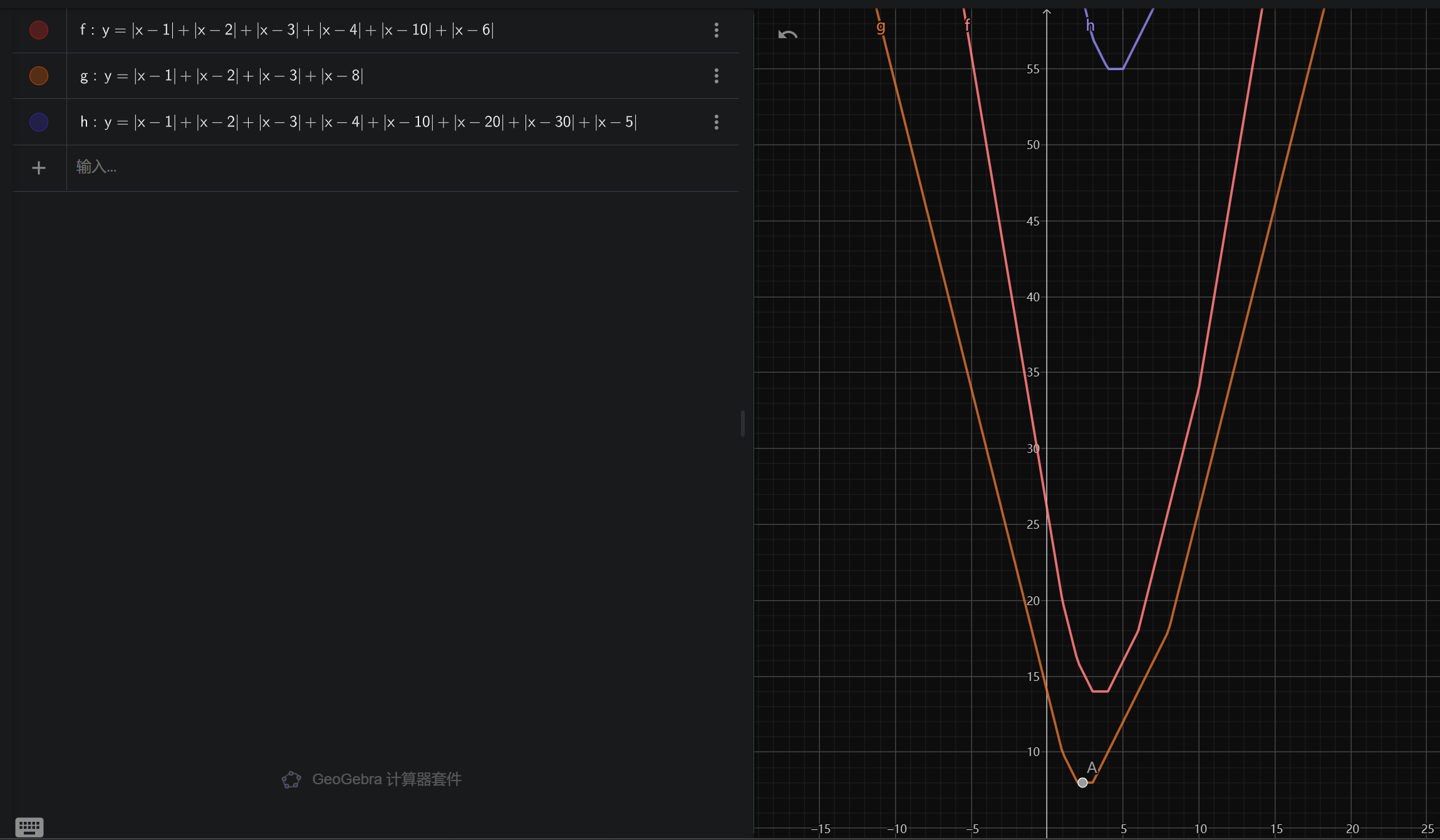
image-20221223163546294

这就有\(w(l,r)\)的求解方法了:

1
2
3
4
5
6
7
w(l,r):
	mid=向下取整((l+r)/2)
	dist_sum=0;
	for all k among [l,r]:
		dist_sum+=abs(x[k]-x[mid])
		
	return dist_sum;

每次调用\(w(l,r)\),时间复杂度都是\(T(r-l+1)=O(n)\)

可以预处理所有的\(w(l,r)\)

1
2
3
4
5
for(int l=1;l<=n;++l){
	for(int r=l;r<=n;++r){
		W[l][r]=w(l,r);
	}
}

外面又套了\(O(n^2)\)的循环

总复杂度是\(O(n^3)\),然而n最大是3000,显然\(O(n^3)\)会超时

如果能给他降为\(O(n^2)\)就可以了

这个\(w[l,r]\)的求法可以继续优化

假设已经知道了\(w[l,r-1]\),现在要求\(w[l,r]\) \[ w[l,r]=w[l,r-1]+x[r]-x[mid(l,r)]\\ mid(l,r)=\lfloor\frac{l+r}{2}\rfloor \] 这条结论看上去很诡异,太简洁了,并且好像中位数的变动只会影响到新加入的第r个村庄,前面的[l,r-1]村庄到邮局的最近距离和仍然是使用的原来的中位数,我自己推导的式子中是有中位数的变化的

如果\(r-l+1\)是一个奇数,那么最右边再加一个,下标中位数不变,相当于邮局位置不用改动,那么[l,r]所有的村庄到这个邮局的距离和不变,\(w[l,r+1]=w[l,r]+|x[r+1]-x[mid]|\)

如果\(r-l+1\)是一个偶数,那么最右边再加一个,下标中位数得往右移动一个,新mid=老mid+1,那么

\(w[l,r+1]=w[l,r]+|x[新mid]-x[老mid]|\times (l-r+1)+|x[r+1]-x[新mid]|\)

再考虑\(r-l+1\)是奇数的情况,如果保持下标中位数不变,实际上对于[l,r+1]时,这个中位数是左中位数

完全可以+1使用右中位数

因此两种情况统一了,即 \[ w[l,r+1]=w[l,r]+(x[mid+1]-x[mid])\times (r-l+1)+x[r+1]-x[mid+1] \]

然而仔细一想确实可以忽略中位数的变化.怎么想呢?

\[ \begin{aligned} w[l,r-1]&=\sum_{l\le k\le r-1}|x[k]-x[mid(l,r-1)]|\\ w[l,r]&=\sum_{l\le k\le r}|x[k]-x[mid(l,r)]|\\ \end{aligned} \] 如果[l,r-1]之间有偶数个村庄,那么选取邮局建立在左中位数村庄或者右中位数村庄,甚至两者直接的地方(虽然只允许建立在村庄里),[l,r-1]所有的村庄到这个邮局的距离和都是最短的,这在图上对应水平谷底那一段

不妨让邮局建立在右中位数村庄,也就是\(\lfloor\frac{l+r-1}{2}\rfloor+1\)

那么[l,r]有奇数个村庄,其中位数唯一,也就是\(\lfloor \frac{l+r}{2}\rfloor\)

由于[l,r-1]之间有偶数个村庄,因此可以设\(r-1-l+1=r-l=2k\)带入上两式 \[ \begin{aligned} \lfloor\frac{l+r-1}{2}\rfloor+1&=\lfloor k+l-\frac{1}{2}\rfloor+1=k+l-1+1=k+l\\ \lfloor \frac{l+r}{2}\rfloor&=\lfloor k+l\rfloor=k+l \end{aligned} \] 这就证明了[l,r]的中位数恰好是[l,r-1]的右中位数,因此两种情况可以选择同一个中位数,因此新加入r村庄的时候w[l,r]直接加上w[l,r-1],无需进行中位数的校正

如果[l,r-1]之间有奇数个村庄,那么只需要让[l,r]选取左中位数和[l,r-1]的中位数是一个点,同理可证

证毕

实际上证完了看这个结论很容易想,但是之前思维就太僵化了,以后记住这个结论吧

加上w计算的优化,加上四边形不懂事的优化

okk,现在dp的时间复杂度成功降到了\(O(n^2)\)

优化后的w,其计算的时间复杂度也是\(O(n^2)\)

总时间复杂度就是\(O(n^2)\)

应该可以通过了吧

不想写了,开摆,明天写了题解然后再看看四边形不懂事优化

阳了四天,摆了四天...

首先是不加四边形不等式优化的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
#include <iostream>
#include <algorithm>
using namespace std;
int v, p;
const int INF = 1e9;
const int maxv = 3010;
const int maxp = 310;
int x[maxv];
int w[maxv][maxv];
int dp[maxv][maxp];
// int s[maxv][maxp];
int s[maxv];
int main()
{
    // cin.tie(0);
    cin >> v >> p;
    for (int i = 1; i <= v; ++i)
    {
        cin >> x[i];
    }

    sort(x + 1, x + v + 1);//使村庄的坐标升序排列

    //初始化w数组
    for (int l = 1; l <= v; ++l)
    {
        w[l][l] = 0; // 从l号村庄上建立邮局,到该村庄的最短邮局距离就是0
        for (int r = l + 1; r <= v; ++r)
        {
            w[l][r] = w[l][r - 1] + x[r] - x[(l + r) >> 1];
        }
    }


    //初始化dp数组
    for (int i = 0; i <= v; i++)
    {
        s[i]=i;
        for (int j = 0; j <= p; ++j)
        {
            dp[i][j] = INF;
        }
    }
    dp[0][0] = 0;

    
    for (auto j = 1; j <= p; ++j)
    {
        for (auto i = 1; i <= v; ++i)
        {
            int temp_min = INF;
            for (auto k = s[i-1]; k < i; ++k)
            {
                if(temp_min>dp[k][j - 1] + w[k + 1][i]){
                    temp_min=dp[k][j - 1] + w[k + 1][i];
                    s[i]=k;//四边形不等式优化
                }
                // temp_min = min(temp_min, dp[k][j - 1] + w[k + 1][i]);
            }
            dp[i][j] = temp_min;
        }
    }

    // i,j遍历顺序反了,导致计算dp[i][j]时,dp[k][j-1]可能还没有经过计算
    //  for(auto i=1;i<=v;++i){
    //      for(auto j=1;j<=p;++j){
    //          int temp_min=INF;
    //          for(auto k=1;k<i;++k){
    //              temp_min=min(temp_min,dp[k][j-1]+w[k+1][i]);
    //          }
    //          dp[i][j]=temp_min;
    //      }
    //  }
    cout << dp[v][p];

    return 0;
}

动态规划-四边形不等式优化

证明及其他详细资料见luoyongjun999/code: code (github.com)

区间dp的状态转移,一般长这样(以P1775石子合并为例):

1
2
3
4
5
6
7
8
9
10
11
12
13
for(int delta=1;delta<=n;++delta){
    for(auto i=1;i+delta<=n;++i){
        auto j=i+delta;
        int temp_min=INF;
        for(auto k=i;k<j;++k){
            if(dp[i][k]+dp[k+1][j]<temp_min){
                temp_min=dp[i][k]+dp[k+1][j];
                s[i][j]=k;
            }
        }
        dp[i][j]=temp_min+prefix[j]-prefix[i-1];
    }
}

三层循环,复杂度\(O(n^3)\)

使用四边形不等式优化(能够证明成立的前提下),可以将最里圈k的遍历范围从\([i,j)\),缩减到\([s[i][j-1],s[i+1][j]\),这个范围结合上i和j的范围能够证明,三层循环的时间复杂度实际上是\(O(n^2)\)

这里\(s[i][j]\)的实际意义是,当\(dp[i][j]=\min_{i\leq k<j}(dp[i][k]+dp[k+1][j])+\sum_{i\leq k\leq j}a[k]\)在k处取得最小值时,此时的k就作为\(s[i][j]\)

边界条件是\(s[i][i]=i\)

用法见P1775

P1775 石子合并（弱化版)

一排N堆石头第i堆石头有a[i]个,合并两堆石头的得分是两堆石头的数量和

求最后合并只剩一堆时取得的最小得分,其中\(N\le 300,a[i]\leq 1000\)

P1880那个题是环状的,这个是线性的

设计状态: \[ dp[i][j]表示合并[i,j]所有的石子,获得的最小得分 \] 边界条件: \[ dp[i][i]=0,即合并一堆时合并个寂寞 \] 状态转移: \[ dp[i][j]=\min_{i\leq k<j}(dp[i][k]+dp[k+1][j])+\sum_{i\leq k\leq j}a[k] \] 前缀和优化: \[ \sum_{i\leq k\leq j}a[k]=prefix[j]-prefix[i-1]\\ dp[i][j]=\min_{i\leq k<j}(dp[i][k]+dp[k+1][j])+prefix[j]-prefix[i-1] \] 四边形不等式优化:

实际上需要证明\(dp[i][j]\),但是可以证明只要是\(w[i][j]\)满足四边形不等式,\(dp[i][j]\)也自动满足四边形不等式,

因此首先证明\(w[i][j]=\sum_{i\leq k\leq j}a[k]=prefix[j]-prefix[i-1]\)满足应用四边形不等式的条件,即证:

1.定义:对于任意\(i<i+1\leq j<j+1\),都有 \[ w[i][j]+w[i+1][j+1]\leq w[i][j+1]+w[i+1][j] \] 2.单调性:对于任意\(i\le i'\le j\le j'\),都有 \[ w[i][j']\ge w[i'][j] \] 证明如下:

对于定义: \[ w[i][j]+w[i+1][j+1]=prefix[j]-prefix[i-1]+prefix[j+1]-prefix[i] \]

\[ w[i][j+1]+w[i+1][j]=prefix[j+1]-prefix[i-1]+prefix[j]-prefix[i] \]

左=右,定义成立

对于单调性: \[ w[i][j']-w[i'][j]=prefix[j']-prefix[i-1]-prefix[j]+prefix[i'-1]\\ =(prefix[j']-prefix[j])+(prefix[i'-1]-preifx[i-1]) \] 由于\(i\le i'\le j\le j'\),并且前缀函数\(prefix[i]\)单调不减,因此上式非负,即 \[ w[i][j']\ge w[i'][j] \] 证毕

下面就可以使用四边形不等式的性质定理优化了

\[ dp[i][j]=\min_{s[i-1][j]\leq k<s[i][j+1]}(dp[i][k]+dp[k+1][j])+prefix[j]-prefix[i-1] \] 这里\(s[i][j]\)的实际意义是,当\(dp[i][j]=\min_{i\leq k<j}(dp[i][k]+dp[k+1][j])+\sum_{i\leq k\leq j}a[k]\)在k处取得最小值时,此时的k就作为\(s[i][j]\)

边界条件是\(s[i][i]=i\)

\(s[i][j]\)的计算并不是头铁地从i到j遍历k先求\(s[i][j]\),而是跟随dp一起求

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <iostream>
#include <algorithm>
using namespace std;
const int maxn=310;
const int INF=1e9;
int n;
int a[maxn];
int dp[maxn][maxn];
int s[maxn][maxn];
int prefix[maxn];


int main(){
    cin>>n;
    for(int i=1;i<=n;++i){
        cin>>a[i];
        s[i][i]=i;
        dp[i][i]=0;
        prefix[i]=prefix[i-1]+a[i];
    }
    for(int delta=1;delta<=n;++delta){
        for(auto i=1;i+delta<=n;++i){
            auto j=i+delta;
            int temp_min=INF;
            for(auto k=i;k<j;++k){
                if(dp[i][k]+dp[k+1][j]<temp_min){
                    temp_min=dp[i][k]+dp[k+1][j];
                    s[i][j]=k;
                }
            }
            dp[i][j]=temp_min+prefix[j]-prefix[i-1];
        }
    }
    cout<<dp[1][n]<<endl;
    return 0;
}

至于四边形不等式的正确性,现在还没有完全转阴,啥时候脑子不浑了再看吧...