计算机网络-数据链路层

数据链路层

数据链路层的任务

数据链路层的功能:成帧,流量控制,差错控制,通信

成帧:多个数据帧之间如何区分?添加标志位,比如011111,如果接收方发现一个0后面连着5个1,就认为这和刚才接收到的数据不是一个帧的.

流量控制用于,限制发送方在等到确认之前发送的数据数量

差错控制指望重发,说官话就是"自动重复请求"(ARQ,Automatic Repeat Request)

冗余编码

冗余:Redundancy

冗余本是多余的意思,在计算机中,冗余量和业务逻辑无关,没有冗余照样执行业务

但是冗余可以增强非业务性能,比如信息论上的冗余可以提高发现错误和纠正错误的能力

考虑8个工件有一个坏件,质量和其他的不同(具体重了还是清了不知道)

最快多少次找到?这实际上就是尽量减少冗余,尽最大可能利用信息熵的问题

采用二分需要单调性,即知道这个坏件轻了还是重了,现在不知道,没法二分

三分?3v3v2,还是那个问题,3v3不知道哪个是标准

四分?(2v2)v(2v2).其中必有一组2v2都是标准件,天平平衡

不妨设前一个2v2平等,说明坏件一定在后面的2v2中,并且前面四个都是标准件,可以用来参考

后面的2v2就不用称了,每个2直接和两个标准件比较

必然有一组不平衡,这就意味着另一组必定平衡,从不平衡组任意拿出一个,和标准件对比

如果是坏件则天平不平衡,否则如果是好件,则同组另一件必定坏件

块编码

数据字+冗余=码字

什么思想呢?

假如原来要传输一个比特,要么是0要么是1

但是路上可能发生各种变故导致1变成0.但是接收方不知道发生了变故,它认为人家就是发送的0,于是错误接收了0

为了增加检错能力

添加一位冗余,比如数据字为0,码字就为00.数据字为1,码字就为11

这样如果有一位发生突变(认为两位同突变的概率低),会形成01或者10这种无效码字,发现错误

那么问题又来了,如果接到01,怎么确定它是00还是11变来的?两者都只需要突变一位就能形成01,因而只添加一位冗余无法纠错

于是再添加一位冗余,只有000和111合法

那么接到100,认为它是000突变来的,这个概率要比他是从111突变来的大.

于是就有了纠错能力.

实际上的块编码,是多位为一个数据字

整个报文划分为弱干块,每块k位,称为数据字

每块中假如r个冗余位,块长度变为n=k+r,形成这个n位的块叫做码字

码字有$2^n$种,但是其中实际承载数据字的只有$2^k$种

如果一个承载数据的码字,其中的一位或者几位发生突变,突变之后的码字:

如果如果不承载数据,则可以被检错

如果也是承载数据的码字,则无法检错

比如4B/5B编码(部分)中:

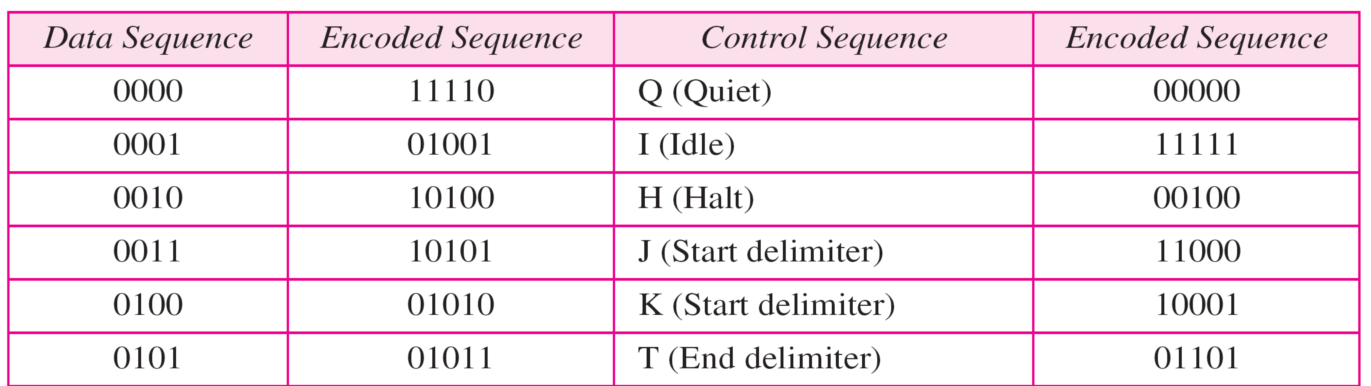
如果0100的编码01010最后一位发生突变,编程了01011,这是0101的编码.那么错误就检查不出来了,接收方会认为发送方一开始就是发的0101

下面推导,检错能力和纠错能力的条件是什么

汉明距离

假设只有一位突变

如果两个有效码字只有一位不同,这样不具备检错能力

如果任何两个有效码字至少有两位不同.这样才具备检错能力,但是不具备纠错能力

如果任何两个有效码字至少有三位不同.这样才具备纠错一位的能力,也可以检错两位

定义两个长度相同的字x,y的汉明距离是对应位不同的数量,记作$d(x,y)$ \[ d(x,y)=x\oplus y 结果中1的数量 \] 最小汉明距离:一组字所有对中最小的汉明距离

编码方案

块编码方案记为$C(n,k)\ with\ d_{min}=x$

其中n是码字长度,k是数据字长度.$d_{min}$是有效码字的最小汉明距离

当可以检错$s$个错误时,要求$d_{min}=s+1$

当可以纠错$s$个错误时,要求$d_{min}> 2s$,也就是$d_{min}=2s+1$

因此最好采用奇数长度的码字

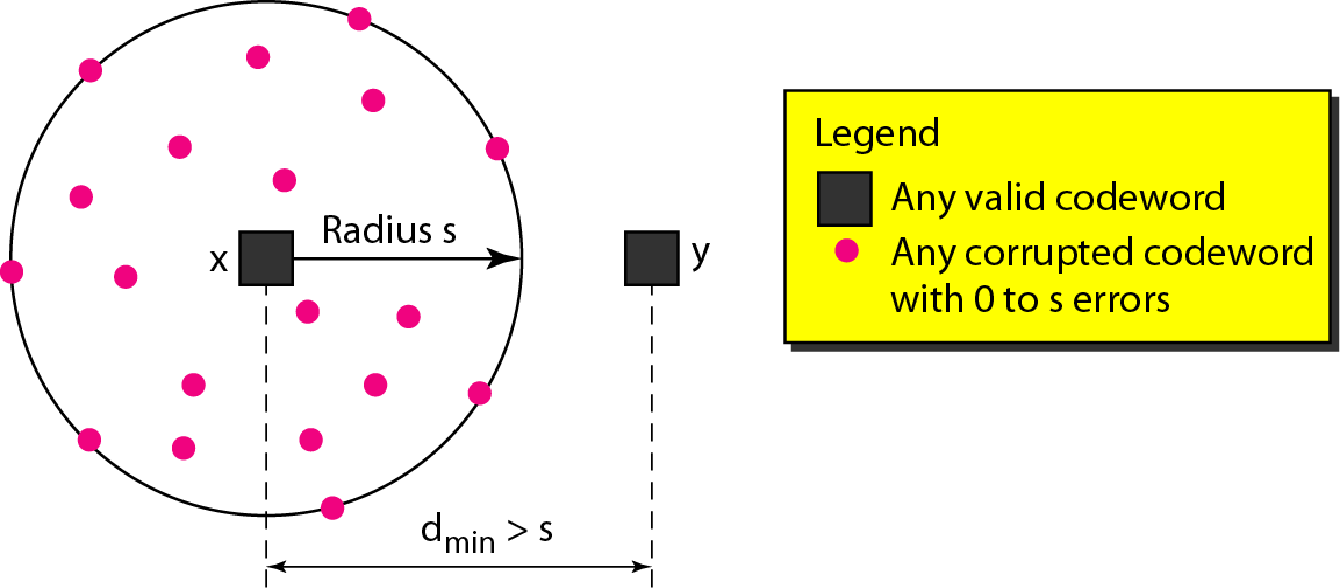
x和y两个有效码字,有相同的概率突变为同一个错误码字,因而无法纠错

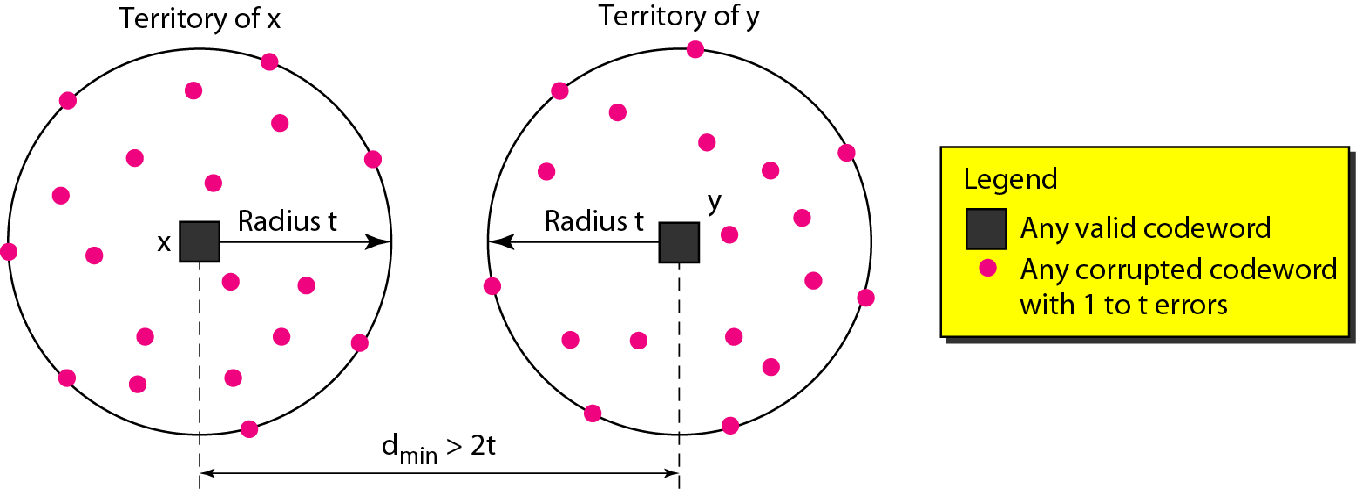
x突变s位之后依然落在半径为s的圈里,而任意两个圈相离,也就是说一个错误码字一定有一个概率最大的突变来源.

这就有了纠错能力

线性块编码

线性块编码:任何两个有效码字的异或生成另一个有效码字.比如:

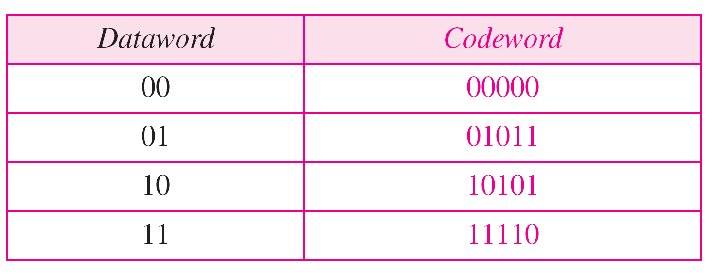
最小汉明距离

线性快编码的最小汉明距离:1的个数最少的非零有效码字中的1的个数

还是以上图为例

非零码字	1的个数
01011	3
10101	3
11110	4

因此$d_{min}=3$

简单奇偶校验编码

$n=k+1,d_{min}=2$

只有一位校验位

比如$C(5,4)$

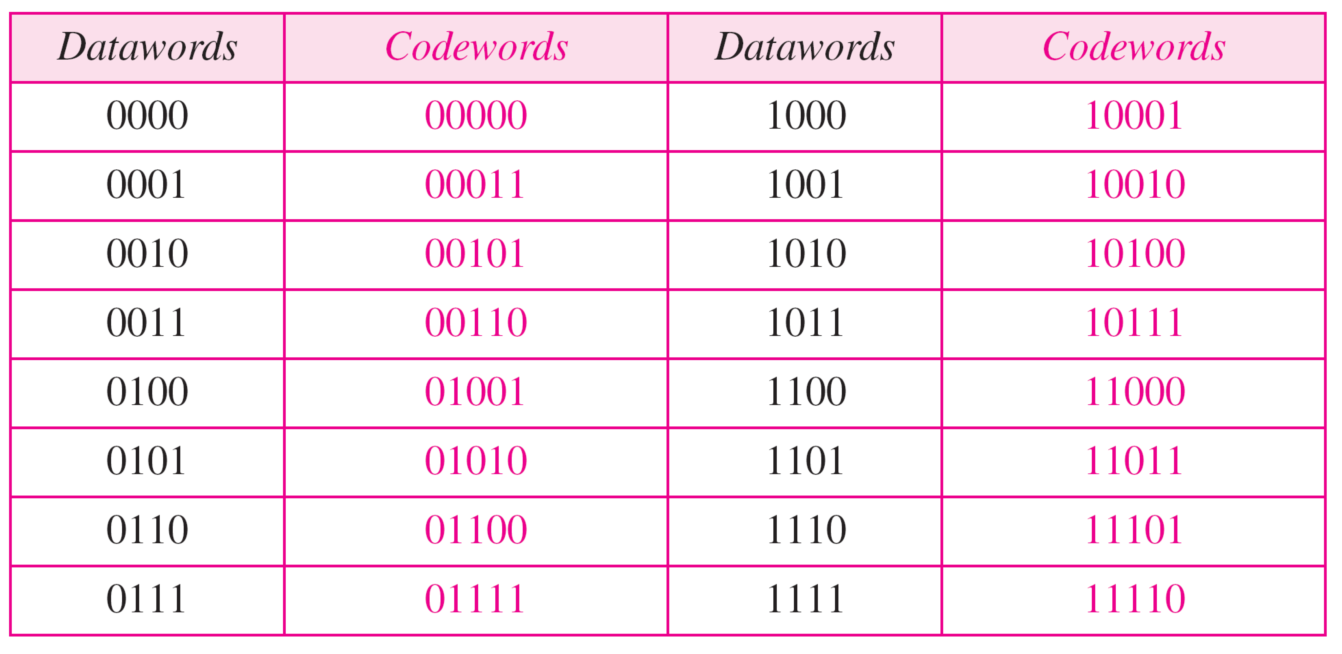
突变奇数位可以被检查出

突变偶数位不可以

二维奇偶校验

两维奇偶校验能检测出所有3位或3位以下的错误（因为此时至少在某一行或某一列上有一位错）、奇数位错以及很大一部分偶数位错。

汉明编码

对于汉明编码$C(n,k),d_{min}=3$,有如下关系: \[ \begin{cases} n=2^m-1\\ k=n-m\\ r=m \end{cases} \] 比如$C(7,4)$中,$n=7=2^m-1$得到m=3

$k=n-m=7-3=4$即数据字位数

$r=m=3$即冗余位数

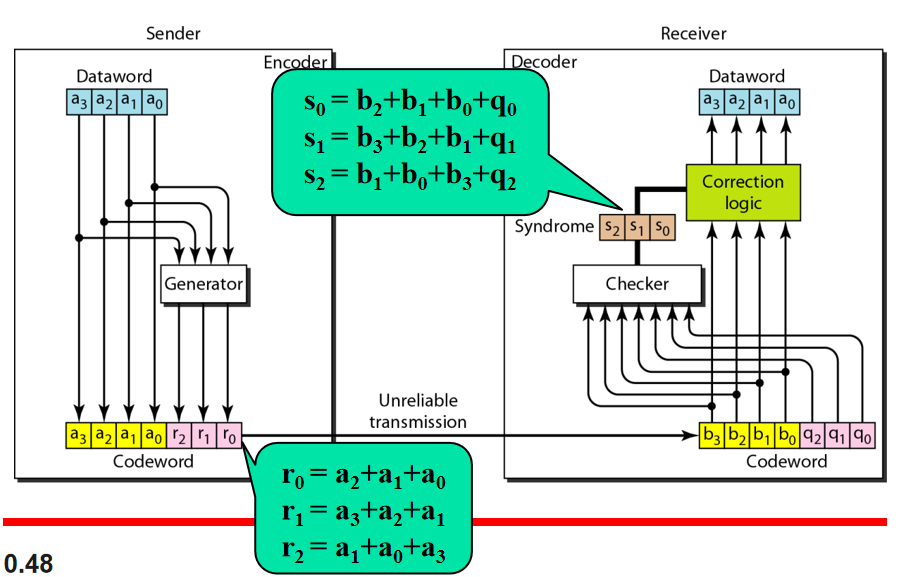
如何检错?

比如数据字0111,计算冗余校验位: $$ \[\begin{cases} r_0=a_2+a_1+a_0=1+1+1=1\\ r_1=a_3+a_2+a_1=0+1+1=0\\ r_2=a_1+a_0+a_3=1+1+0=0 \end{cases}\]

$$ 得到码字$0111001$

如果码字没有错误,那么接收方计算得到的q2q1q0应该全零

如果码字有一位出现错误,变成$0110001$

在接收方(接收方认为顶多有一位发生错误): \[ q_0=b_2+b_1+b_0+q_0=1+1+0+1=1 \] 此时已经发现错误了,但是不能确认是b2,b1,b0,q0这四位中的哪一位出现的差错

然后又算得 \[ q_1=b_3+b_2+b_1+q_1=0+1+1+0=0 \] 说明b3b2b1q1都没错误,那么只有b0,q0中有错误

然后又算得 \[ q_2=b_1+b_0+b_3+q_2=1+0+0+0=1 \] 可以肯定是$b_0$的错误了

如果数据字至少是7位,计算满足一位检错条件的汉明编码方案 \[ \begin{cases} n=2^m-1\\ k=n-m\\ r=m \end{cases} \]

\[ k=n-m=2^m-1-m\ge7 \]

解得

$m=4,n=15,k=11$

因此满足条件的编码方案是$C(15,11)$

循环冗余编码

Cyclic Redundancy Check,CRC

$C(n,k)$

n位的码字,其中k位数据字,最右边加上n-k个0作为校正子的初始值,这样n位传递给生成器

生成器用长度n-k+1的除数去除码字

得到n-k位余数,填到校正子上

真码字(数据字:校正子)就计算完毕了,然后传输,然后被接收

接收方校验器用相同除数除码字

如果得到n-k位余数是0则无误,码字前k位就是数据字

否则丢弃

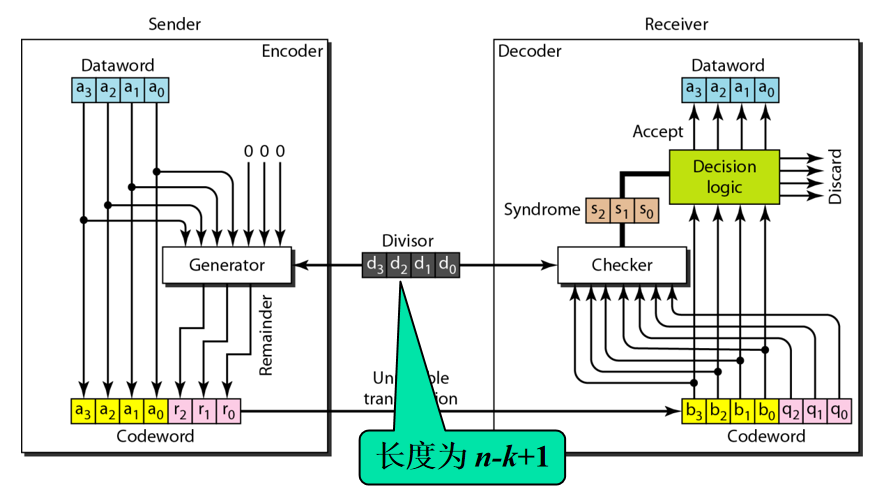
计算过程

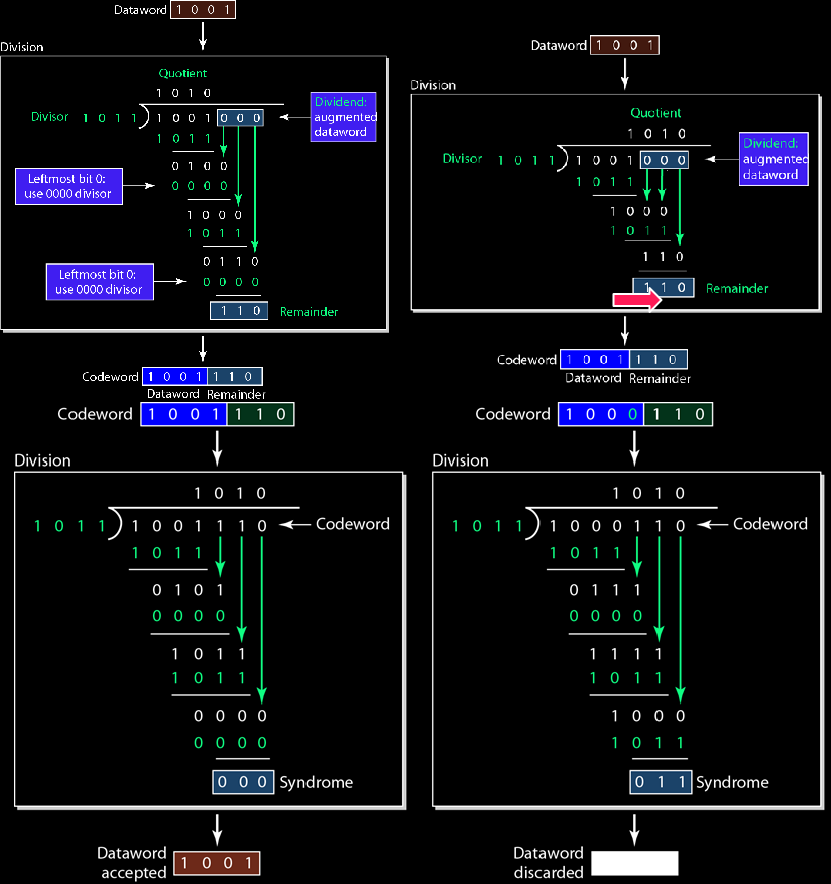
多项式

CRC的除数称为生成多项式,简称生成子或者生成器$g(x)$

码字$c(x)=d(x):s(x)$,码字就是数据字和校正子的增广

差错$e(x)$

校验原理:

在发送端计算完的真码字一定满足$\frac{c(x)}{g(x)}=0$

因此对接收方的码字除以$g(x)$,如果不为零,说明一定存在$\frac{e(x)}{g(x)}$这一项,也就是说分子不为零,即存在$e(x)$这一项,即存在差错

生成多项式的形式决定了检错能力

单个位差错

单个位差错是指$e(x)=x^i$的情形

检测单个位差错需要保证$e(x)$不能被$g(x)$整除

比如如果设置$g(x)=1$,则任何多项式都被$g(x)$整除,这就查不出任何错误来

如果生成多项式至少有两项,并且有1这一项(也就是$x^0$这一项),那么所有单比特错误都可以检出

也就是说,$g(x)$的作用是,出现差错时,$e(x)$无法被$g(x)$整除

两独立位差错

两独立位差错指$e(x)=x^i+x^j$的情形 \[ e(x)=x^i+x^j=x^i(x^{j-i}+1)=x^i(x^t+1) \] 如果生成多项式$g(x)$无法整除$x^t+1$则所有独立两位错误都可以检查出来

比如$x+1$不能检查出两个相邻位的错误

$x^4+1$无法检查出两个相隔4位的错误

$x^3+x^2+1$就可以检查所有两个独立位错误

奇数个位差错

奇数个位错误指: \[ e(x)=x^{i1}+x^{i2}+...+x^{ik} \] 其中k是奇数

只要是$g(x)$包含$x+1$因式,就可以检查出$e(x)$,证明:

如果任何一个偶数项多项式都可以被$x+1$整除,那么任何奇数项多项式,就可以拆成一个偶数项多项式加一个单独的多项式.那么问题转化为单个比特错误

于是只需要证明任何偶数项多项式可以被$x+1$整除

由于任何偶数项多项式,都可以转化为若干个这种形式的和 \[ x^a(x^t+1) \]

由于多项式系数在模2域上,因此上式又可以写为 \[ x^n(1-x+x^2-x^3+...)=x^n\frac{1-(-x)^t}{1-(-x)} \] 当t是奇数时由上式得到 \[ x^t+1=(x+1)(x^{t-1}-x^{t-2}+x^{t-3}-...) \] 当t不是奇数,是偶数比如$e(x)=x^2+1$,此时t=2是偶数

这就可以利用系数在模2域上的性质了

此时$e(x)=x^2+1=x^2+2x+1=(x+1)^2$

推广一下,可以得到$x^t+1=(x+1)^t$其中t是偶数,并且系数在模2域上

这就证明了$x+1$整除任何偶数项多项式

突发性错误

突发恶疾指接连几个bit位都可能发生错误 \[ e(x)=x^j+...x^i=x^j(1+...+x^{i-j}) \] 令$e'(x)=1+...+x^{i-j}$

意思时,起码两头的i,j两位是有错误的,中间的位可能有错误也可能无误,但是无所谓

设$L=i-j+1$,意思是突发性错误的长度

这L位中,提出公因式$x^j$之后,最低次项是1,最高次项是$x^{i-j}$,这两项肯定得有

设$g(x)=x^r+...+1$表示生成多项式,它至少包含$x^r+1$两项,这保证了可以检测任何单比特错误.其他比r低次的项可有可无.

如果$g(x)$阶比$e'(x)$大,即r>L-1,显然$\frac{e'(x)}{g(x)}$是有余数的,此时任何差错都可以检查出来

如果$g(x)$和$e'(x)$同阶,即r=L-1,

此时只有$e'(x)=g(x)$只有这种情况没有余数,这个概率是多大呢?

要求$g(x)$和$e'(x)$的每一项系数都相同,根据概率论独立事件乘法原则,这个概率是 \[ P(g(x)=e'(x))=(\frac{1}{2})^{L-2}=(\frac{1}{2})^{r-1} \]

这里L-2的原因是,$g(x),e'(x)$最高次项和常数项1都已经是相同的了,只需要考虑中间各项的情况

因此r=L-1时,能够检查出错误的概率是$1-(\frac{1}{2})^{r-1}$

如果$g(x)$比$e'(x)$阶小,即L>r+1时,考虑啥情况检查不出错误?

比如$e(x)=x^6+x^5+x+1$,$g(x)=x^5+1$

此时$\frac{e(x)}{g(x)}=x+1$可以被整除,无法检查出错误

考虑对于任意一个$g(x)$,只要是其阶比$e'(x)$小,一定存在$e'(x)$,使得$g(x)|e'(x)$吗?

确实如此,只需要构造$e'(x)=x^{L-1-r}g(x)+g(x)=(x^{L-1-r}+1)g(x)$

这是一个临界条件,保证了阶是L-1并且存在常数项1

还可以往里随便加$x^kg(x),k\in(0,L-1-r)$项

这样满足条件的构造共有$2^{L-2-r}$种

而L-1阶含常数项1的多项式共有$2^{L-2}$个

因此构造的出现概率就是$\frac{2^{L-2-r}}{2^{L-2}}=(\frac{1}{2})^r$,也就是检不出错误的概率

那么能够检查出错误的概率就是$1-(\frac{1}{2})^r$

总结:

所有$L ≤ r $的突发性差错均可被检测到。

所有$L = r + 1 $的突发性差错有$1 – (1/2)r–1 $的概率被检测到。

所有$L > r + 1 $的突发性差错有$1 – (1/2)r $ 的概率被检测到。

高性能多项式特性

至少有两项,要有常数项1,保证检查一位错误
不能整除 $x^t + 1(2 ≤ t ≤ n − 1)$,保证检查两个独立位错误
应当有因子 $x + 1$,保证检查所有奇数位数错误

校验和

脚丫子都知道怎么算,注意结果要取反

数据链路层协议:

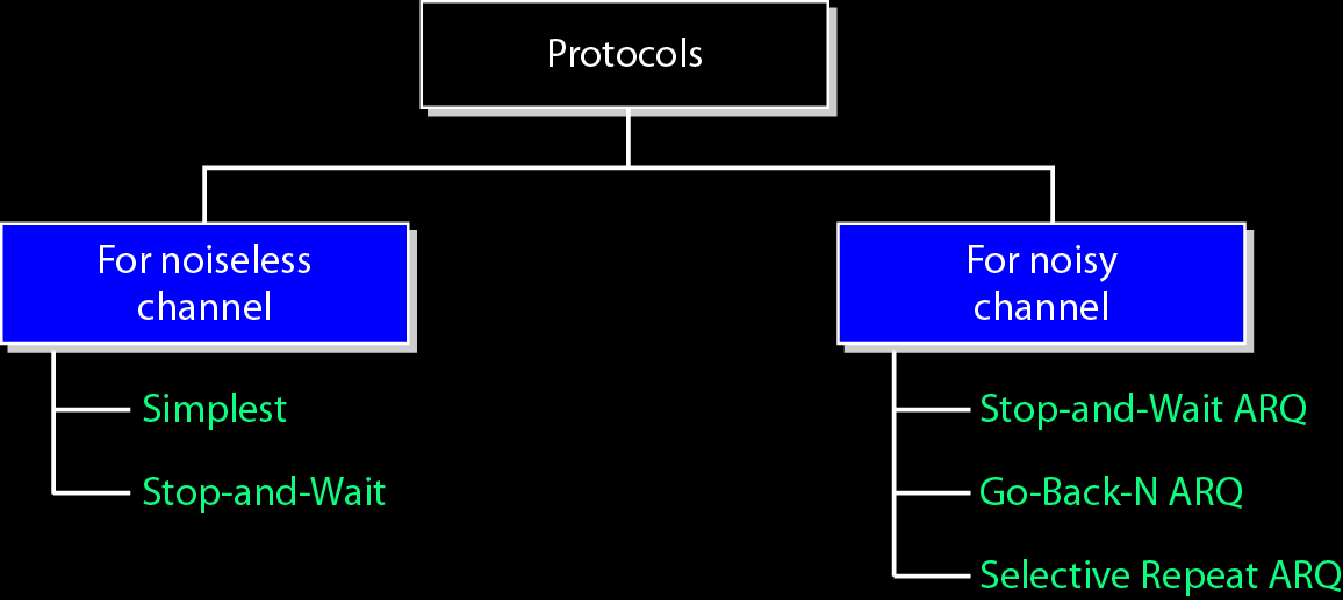
只要带上ARQ的肯定有差错控制功能

noiseless channel是没有噪声,不会丢包,不会重复,无损坏帧的理想信道,最简单协议和停止等待协议只是最初的一厢情愿

协议	特点
simplest	纯纯理想环境, 发送方不需要考虑丢包坏帧的情况,要说啥只说一遍,不多废话接收方就洗耳恭听,也不需要回复收到
stop-and-wait	发送方发一个帧,就等着接收方回复收到如果没有收到回复,那么可能是网络阻塞或者接收方死球了长时间没有收到回复就认为超时了,重发该帧啥时候收到回复确认,啥时候发下一帧

Stop-and-wait ARQ	停等ARQ协议中,每个帧要么编号1要么编号0(原序号模2得到) 如果收到0号帧,则下一个期望的就是1号帧如果接收方接收到的帧不是期望帧,回复自己期望的那一帧已发送的帧会被保留副本,如果超时没有收到该帧的确认(或者说下一帧的期待) 则重发超时帧
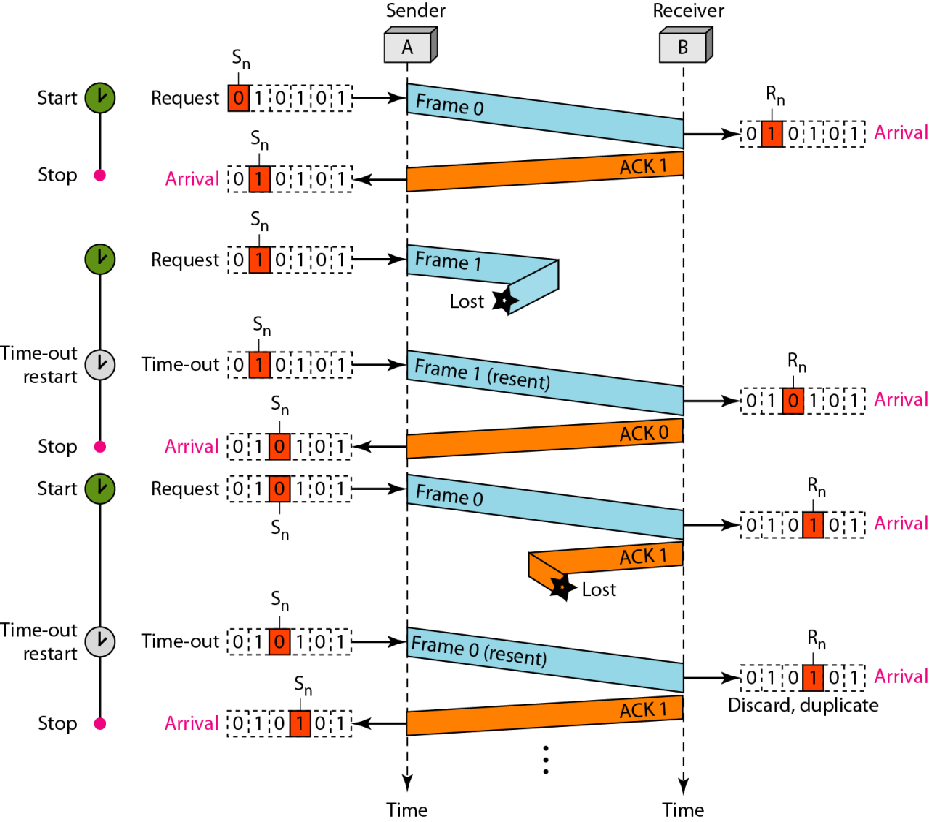Go-Back-N ARQ	实际上是Stop-and-wait ARQ的增强版 Stop-and-wait ARQ协议中没发一个包都要确认一下现在可以发一组包然后确认一下让确认这种控制信息比重更少
Selective Repeat ARQ	Go-Back-N ARQ的增强版 Go-Back-N ARQ中接收方窗口为1, 本算法中将接收方窗口增强到和发送方窗口一样大但是窗口大小更小了,为$2^{m-1}$ (Go-Back-N ARQ中发送方窗口是$2^m-1$)

回退N帧自动重发请求

Go-Back-N Automatic Repeat Request

在帧头部设置一个帧序号字段,假设这个字段使用m位,那么可以编号$[0,2^m)$,即帧序号是模$2^m$的

发送窗口:

发送方的发送窗口大小就设置为$S_{size}=2^m-1$,

为什么要设置成这个值呢?为什么不设置成$2^m$?留作后话

比如帧序号字段占用4bit,那么发送方滑动窗口大小就是16-1=15

两个指针,

其中$S_f$永远指向最早没有被确认的窗口

$S_n$指向当前发送方应该发送的窗口位置

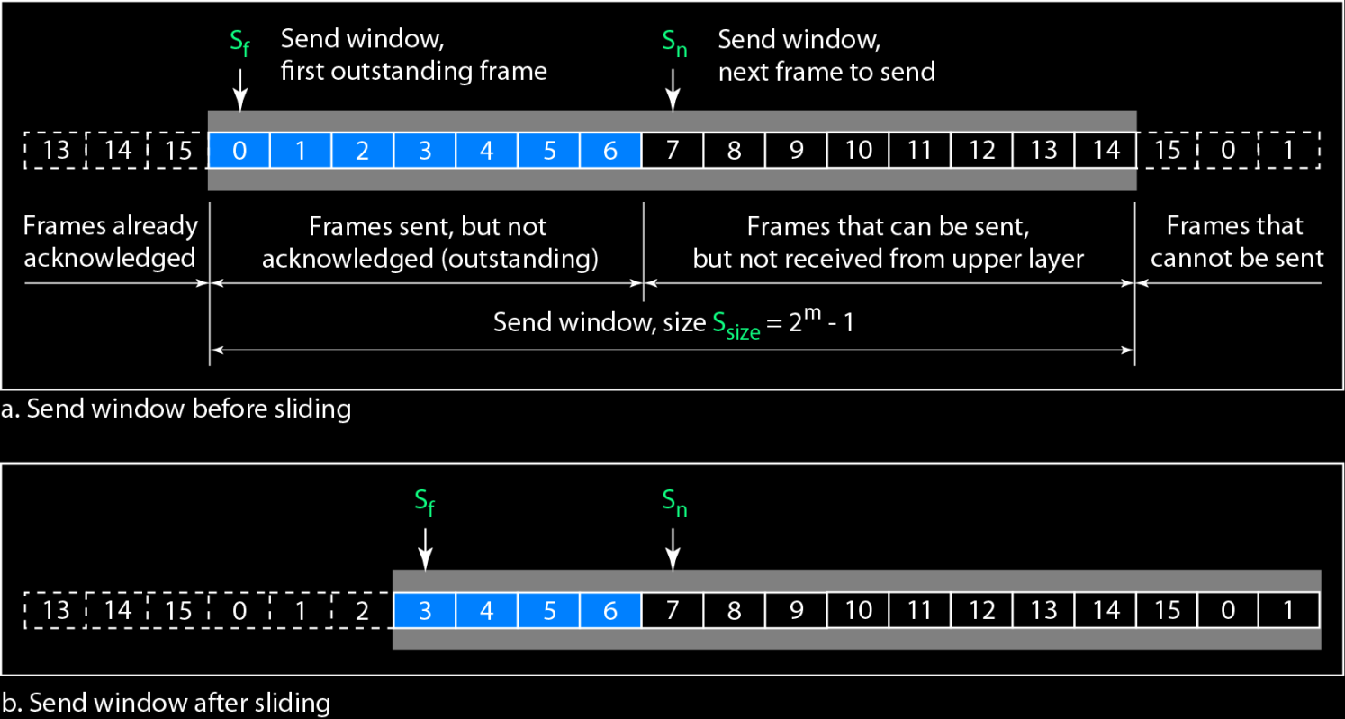
接收窗口:

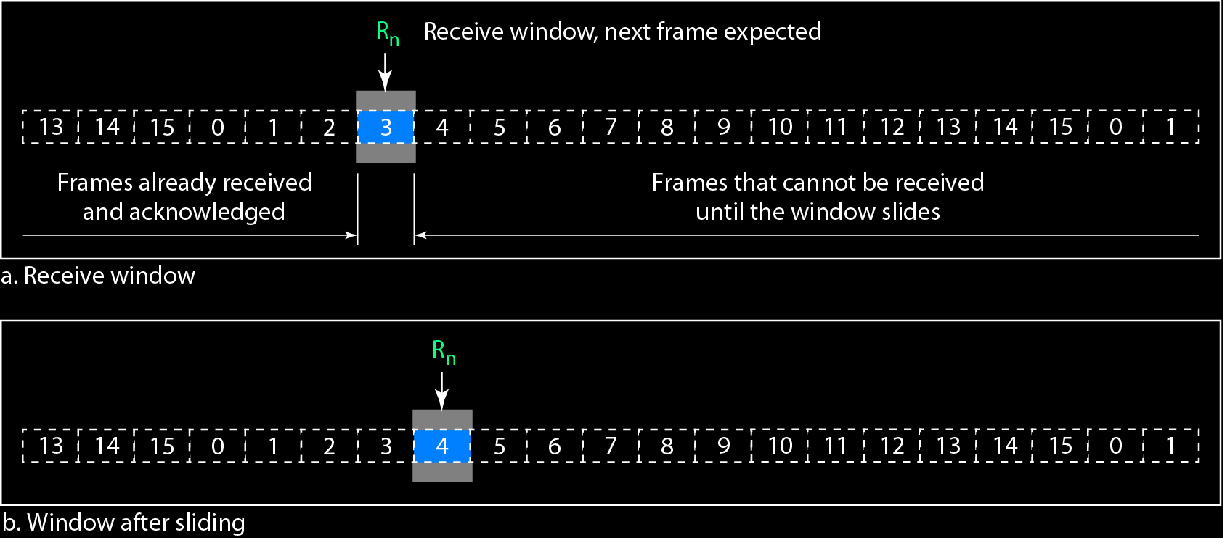
接收方只需要一个指针即可,只需要记录下一个期待接收的窗口

两个窗口如何交互?

假设发送方连续发了0到14帧,这几个帧是陆续到达的,接收方收到第n帧就会回复期待n+1帧.也可能一股脑收到了n,n+1,n+2这三帧,此时接收方直接回复一个累计确认,期望第n+3帧

考虑有丢包,可能接收方对0到5帧的确认都丢了,但是对第6帧的确认没丢,被发送方收到了,这时发送方Sf指针直接移动到第7帧,也就是发送方窗口右移,此时发送方就可以继续发送第15,16,17等等帧了

也可能发送方第0帧就在路上丢包了,第1,2,等等帧都到了,但是接收方不要,就要第一帧,于是接收方直接丢弃并保持沉默,

发送方发现从第0帧往后,一直长时间没有收到回应,就要从第0帧这里开始重发0到14帧

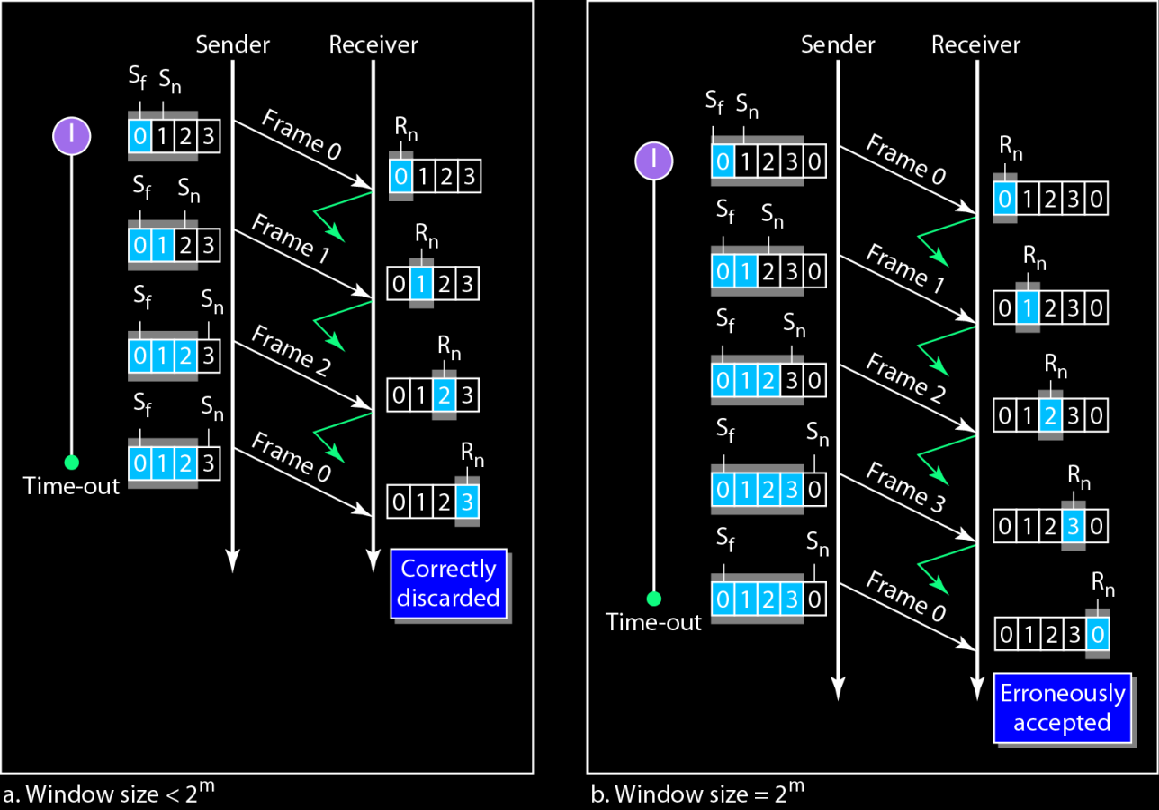
发送方滑动窗口大小设为$2^m-1$的目的

假设m=4,即帧的编号$\in[0,15]$

并且假设滑动窗口大小大于等于$2^m=16$,不妨就设置为16

好,现在一个大文件成帧之后

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15...

滑动窗口要是16就会包含[0,15],假设发送方这16帧全都发出去了,但是网络太垃圾了,没有收到任何回复,而接收方实际上全都回复了,并且接收方已经准备接收下一个0号帧了

此时发送方认为接收方本次[0,15]全都没有收到,于是从0开始重发,但是接收方期望的是下一个0号帧

但是两个帧都是编号0,接收方无法发现错误,于是就错误地接受了

选择性重传

在回退N帧自动重发中只有发送方会累计确认

在选择性重传中,发送方和接收方都会累计确认

解决了啥问题呢?

发送方如果发送了$[0,14]$这些帧,接收方可能就得发送15个确认回复,回复太多这是其一

其二是,如果发送方已经接到了[1,14],唯独0号帧路上丢包了,在回退N帧自动重发中,发送方就得从0开始重发[0,14]

而实际上只需要重发一个0就足够了,但是接收方脑子太小了,只认一个数,[1,14]已经忘记了.

于是就改进成选择性重传算法

接收方加上了窗口,就有了缓存的能力

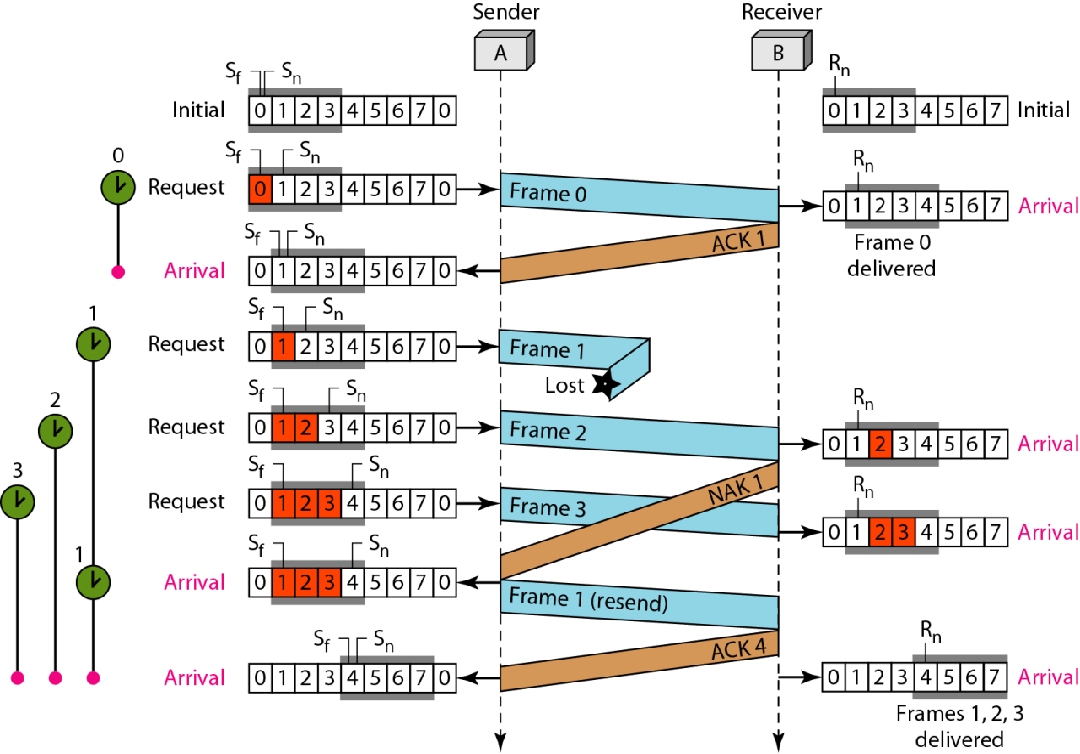
关键注意1号帧在发送途中丢包,但是2号帧顺利抵达,此时接收方回复NAK1,意思是期望1.然而在发送方针对NAK1的回应到达之前,3号帧也顺利抵达了,此时接收方默默收下,但是啥回复都没有

然后发送方的针对NAK1的回复1号帧到了,

此时接收方回复的是ACK4,通知发送方,3之前已经都接收到了,可以发送4及之后的帧了,

发送方接收到ACK4之后会调整自己的发送窗口,然后继续发送4,5,...号帧

为啥发送方和接收方的窗口都得是$2^{m-1}$呢?

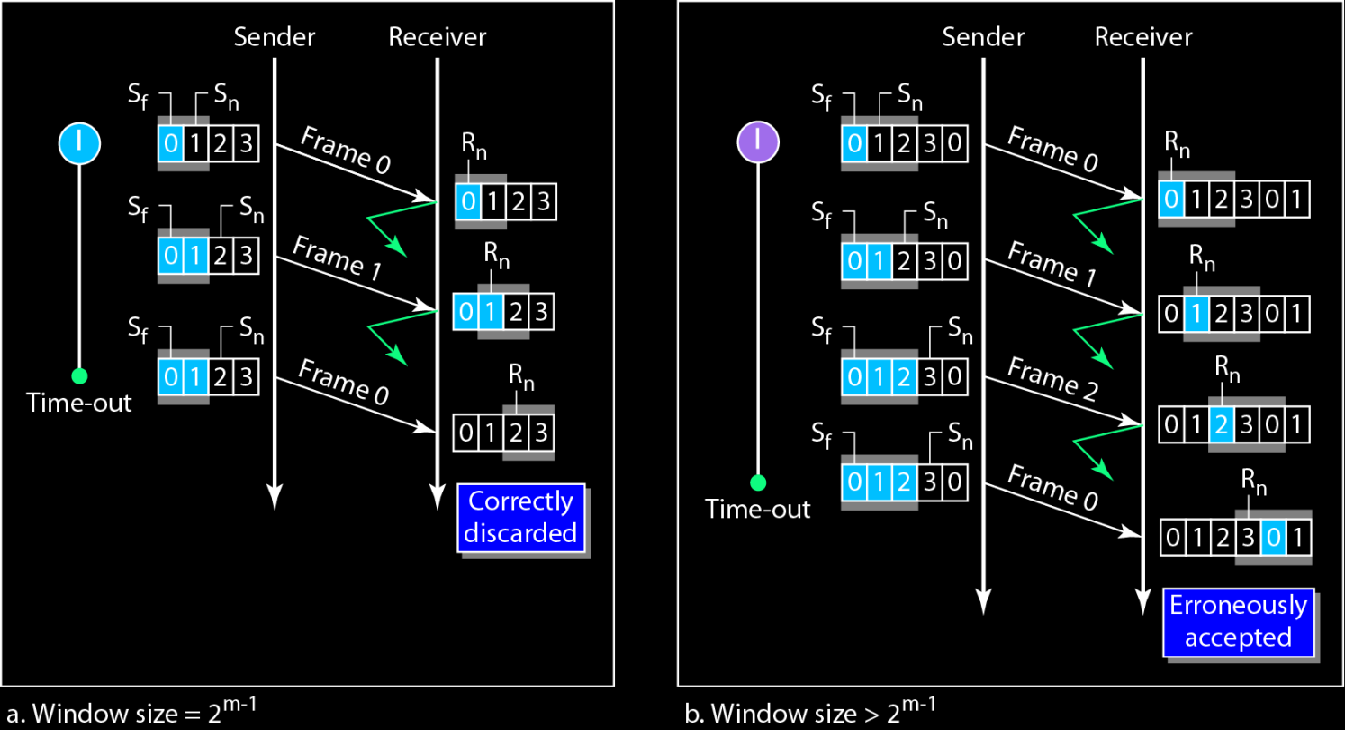
假设m=2,那么帧编号就是$[0,3]$此时窗口大小最大为2,否则,假设是3

发送方发送0,1,2三帧之后,都被接收方收到,但是所有回复都丢包了

此时接收方已经后移了接收窗口,此时接收方窗口内的期待0号帧是下一个0号帧.

但是发送方超时重发了刚才的0号帧

于是接收方就把刚才的0号帧当成下一个0号帧错误接收了

带捎带的N步返回NRQ

捎带:将控制报文,比如NAK,ACK等等,附带到数据报文中一起发送

带宽利用率

首先计算整个链路充满数据,能放开多少数据,也就是带宽时延积

然后使用的协议在传播时间内最多能有多少帧,多少bit上到信道上传输

做比即可

多路访问

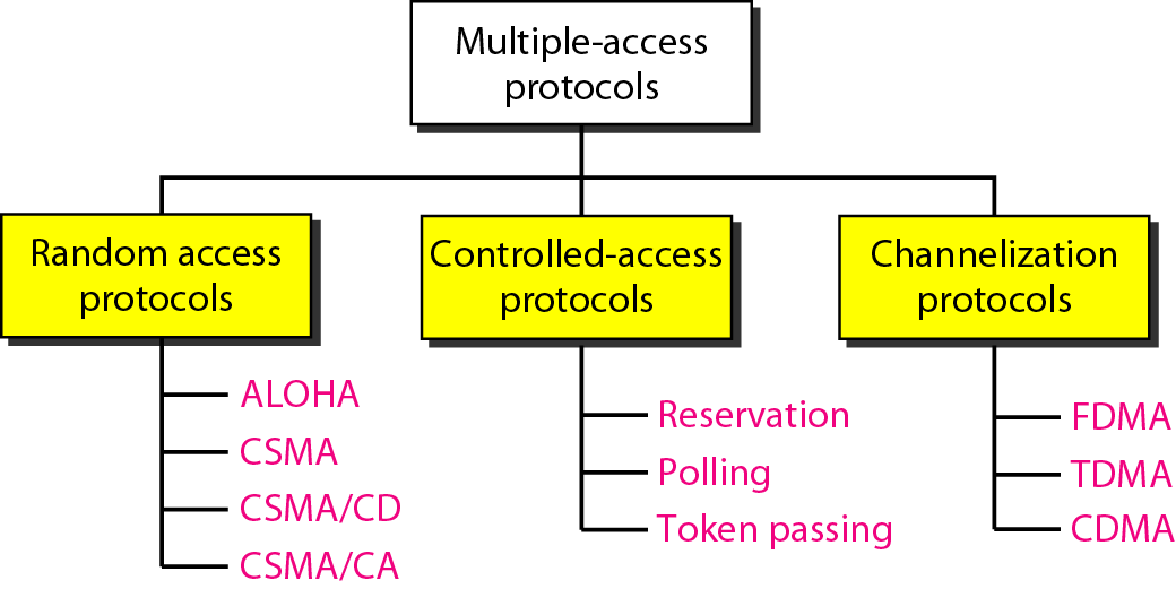
随机访问协议

所有站点低位相同,任何站点都不能组织其他站点说话

有话要说就根据自己的协议说

AlOHA

任何站点,在任何时间,想说啥就说啥

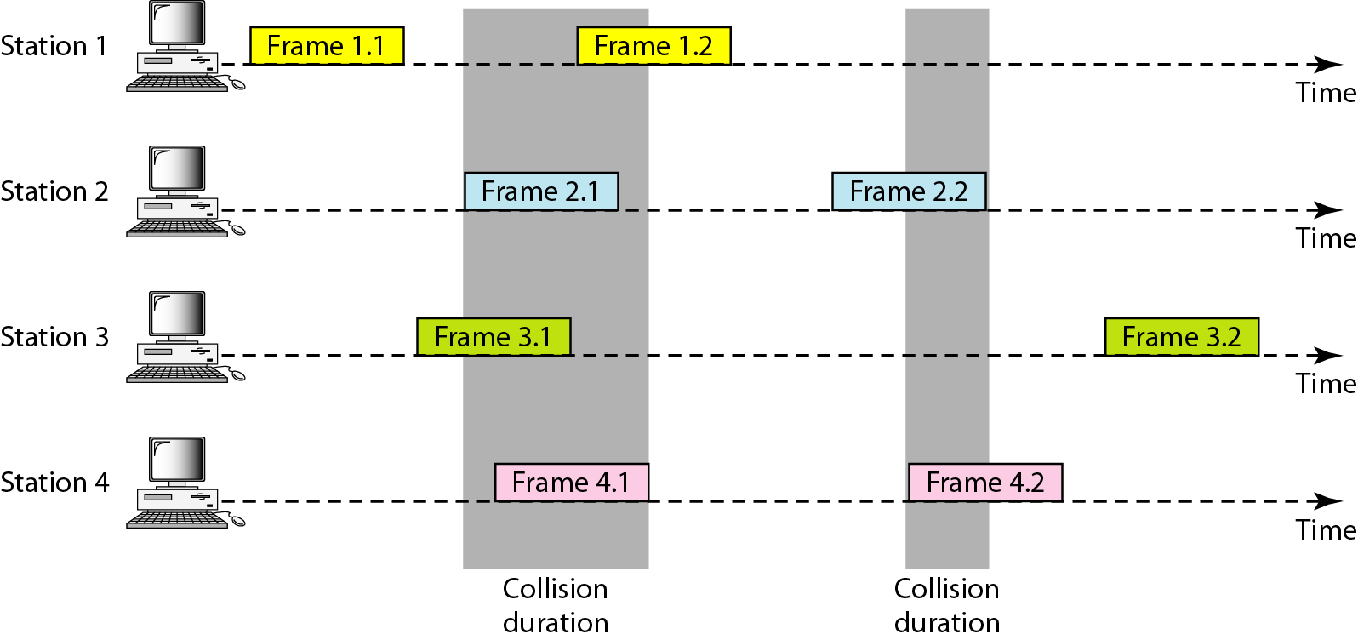
只要同一时间在信道上有两个帧,就会造成冲突,发生冲突的帧都会废掉

ALOHA协议流程:

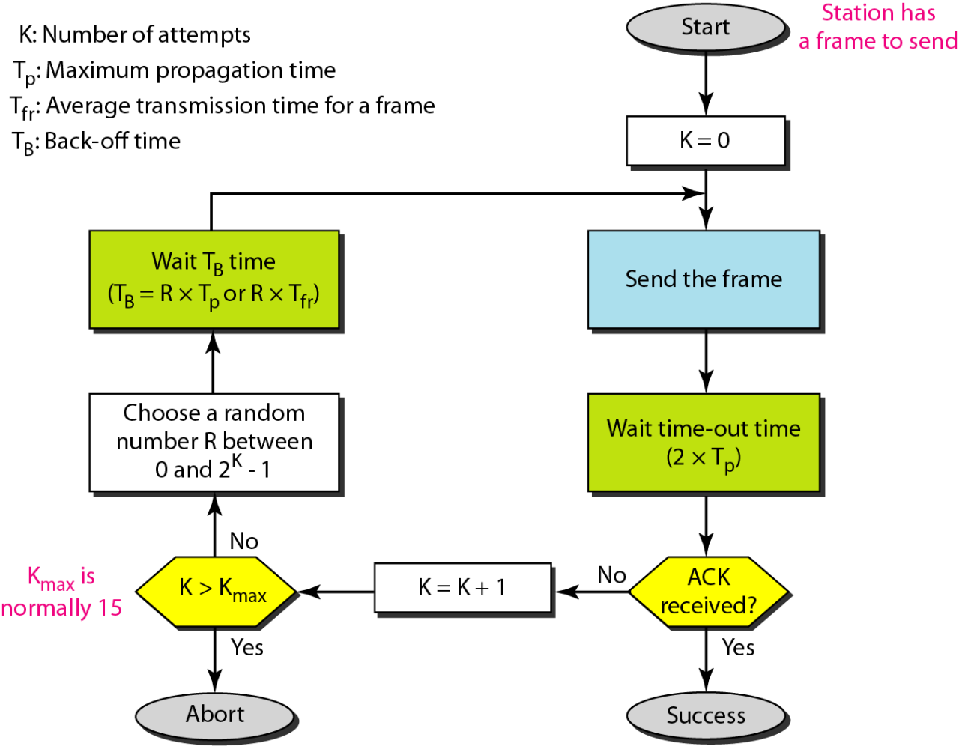
最多重发$K_{max}$次,如果一直没有收到ACK回复则放弃

每次发送之后等待$2\times T_{p}$,这是接收ACK的窗口期

如果没有收到,则等待一个随机数的时间$T_{B}= T_{p}\times R,r\in[0,2^k)$.然后再重发

传输和传播

传输,transmission,又可以翻译为发射,是发送方将信号全放到信道上用的时间 \[ 传输时间=\frac{帧长}{带宽} \]

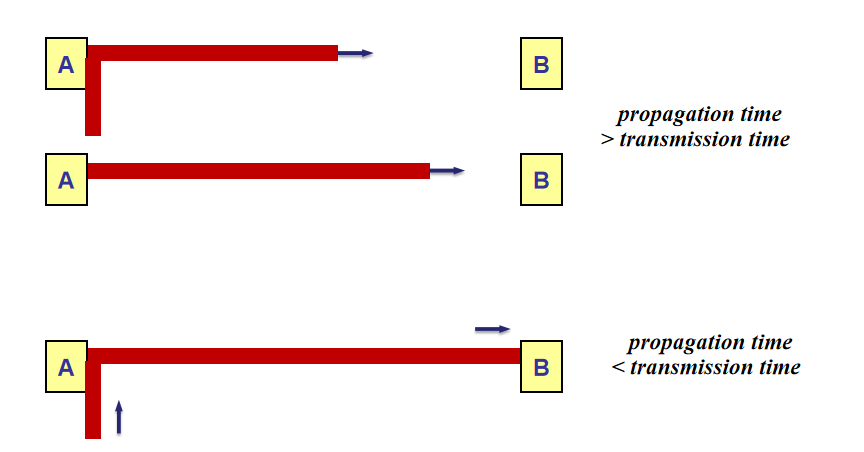
传播,propagation,信号的一位经过信道用时 \[ 传播时间=\frac{电缆长度}{信号速度(一般是光速)} \]

冲突时间:

假设各帧长度相同,ALOHA的冲突时间是传输时间的两倍

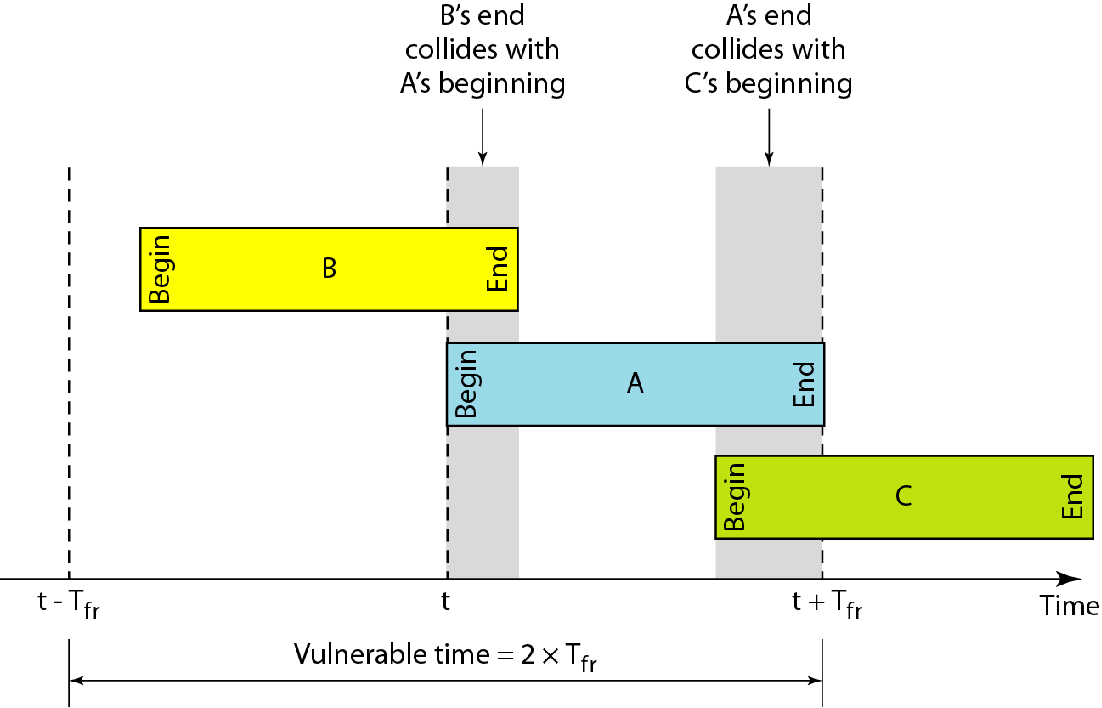
即在$[t-T_{fr},t+T_{fr}]$这期间,不允许有第二个帧

吞吐量

\[ S=G\times e^{-2G} \]

单位:帧

注意这里的吞吐量单位不是bps

当且仅当$G=\frac{1}{2}$,$S_{max}=0.184$

G是帧传输时间内系统平均产生帧的数量

对于$G=\frac{1}{2}$也好立即,因为冲突时间就是两个帧传输时间,如果整个系统在一个传输时间内产生的帧数均值是$G=\frac{1}{2}$,则冲突事件内产生的帧数均值就是1

如果$G>\frac{1}{2}$则冲突的概率增大,一旦发生冲突,两个帧都是废物

而吞吐量的定义是:单位时间内成功传送的数据量.

两个废物帧都不是成功传送,因此导致了吞吐量降低

推导$S=G\times e^{-2G}$

假设传输时间是T,当一个帧发射之后,在T时间内,系统中又发送帧数均值是G

也就是说,T时间内系统又发送一帧的概率为$G$

首先考虑吞吐量怎么计算

定义吞吐量:传输时间内,能够成功传输的帧数,则有: \[ S=GP_0 \] 其中$P_0$为一帧发送成功的概率,也就是冲突时间内没有第二个帧的概率.

$G$是T时间内系统发送帧数的均值

$P_0$是成功率

那么$S=GP_0$就计算了T时间内发送成功的帧数的均值

下面考虑$P_0$怎么算

计算一帧成功传输的概率,也就是发送一帧之后2T时间内没有其他帧的概率

假设T时间内有其他X个帧发射.显然$X\sim P(G)$泊松分布,则分布律为 \[ P(X=k)=\frac{G ^k}{k!}e^{-G} \]

在2T时间即冲突时间内,不发生冲突,意味着没有其他帧发送,其概率是 \[ P(X=0)\times P(X=0)=(\frac{G^0}{0!}e^{-G})^2=e^{-2G} \]

带入$P_0=P(X=0)\times P(X=0)=e^{-2G}$得到 \[ S=GP_0=Ge^{-2G} \]

如果定义吞吐量为:传输时间内成功传输的帧数.那么算到这里就结束了

如果定义吞吐量为:单位时间内成功传输的帧数.那么$S=\frac{G{e^{-2G}}}{T}$

如果定义吞吐量为:单位时间内成功传输的bit数.那么$S=\frac{G{e^{-2G}}}{T}\times 帧大小$

时隙ALOHA

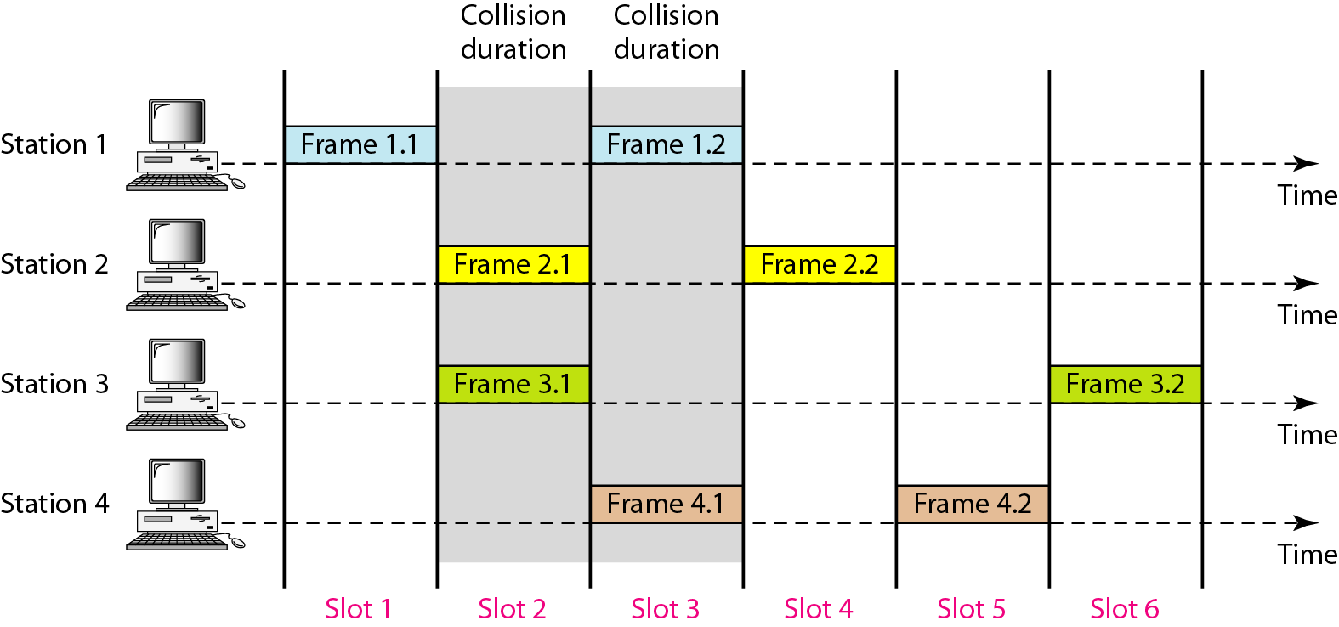
规定只能在每个Slotn一开始发送,每个帧顶多占用一个Slot,不会影响其他Slot

那么冲突只会发生在一个Slot之内,并且一旦发生冲突,一定是两个帧在时间上完全重合

吞吐量

假设每个Slot开始时,系统中传输帧的均值为G帧,则Slot时间内又发送的帧数还是满足泊松分布

只不过冲突时间降为一个Slot,成功发送一帧的概率变为 \[ P_0=P(X=0)=e^{-G} \] 吞吐量就是$S=GP_0=Ge^{-G}$

CSMA

Carrier Sense Multiple Access

载波侦听多路访问

发送前首先侦听,看看有没有其他帧在发送,可以缓解冲突,但是不能解决冲突

因为一个站点侦听时,可能另一个站点已经传输了信号,但是由于传播延迟,没有被本站点侦听到,如图所示:

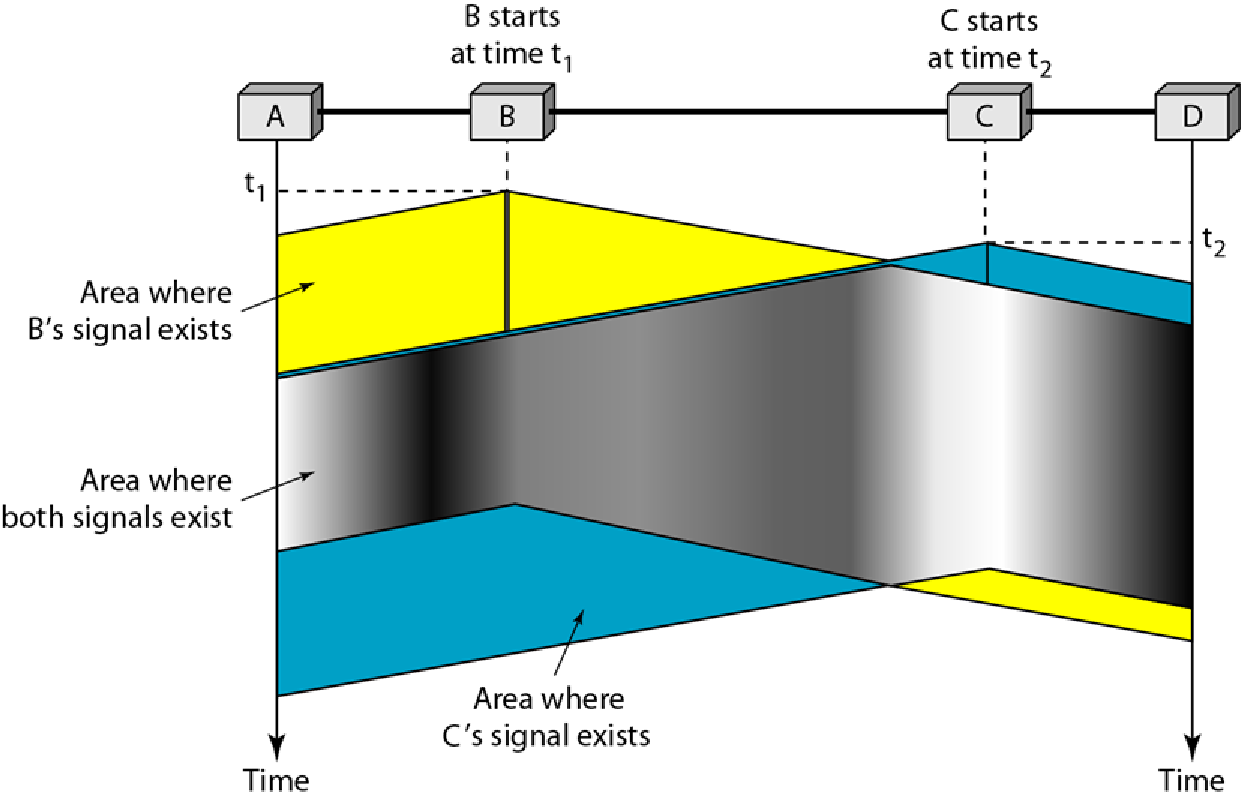
B站点在t1时刻传输一个信号,C在t2时刻要发送一个信号,但是t2时刻信号尚未传播到C处,因此C在t2传输一个信号,就会和B传输的信号发生冲突

冲突时间

在B开始传输消息,到消息传播到其他站点之前,这段时间是不能有第二个消息传播的

因此冲突时间就等于传播时间

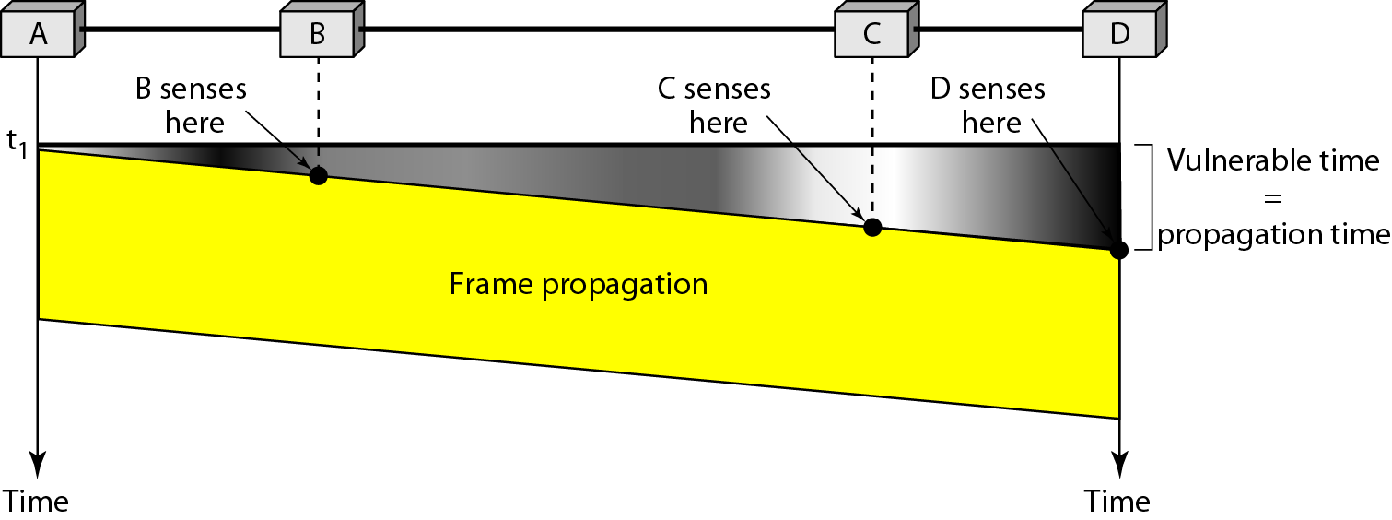
冲突缓解方法

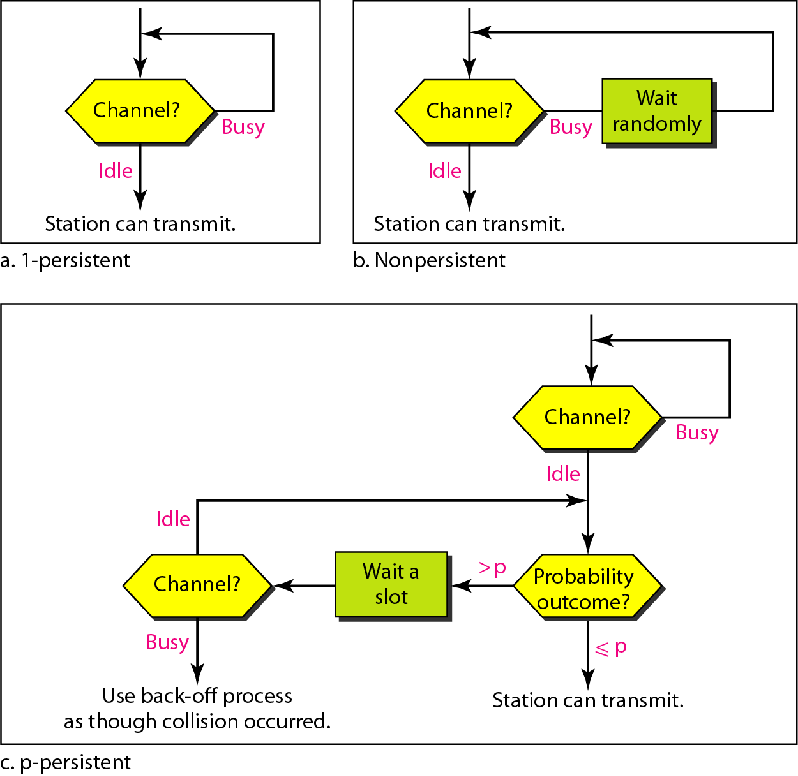
CSMA/CD

Carrier Sense Multiple Access with Collision Detection,带冲突检测的载波侦听多路访问

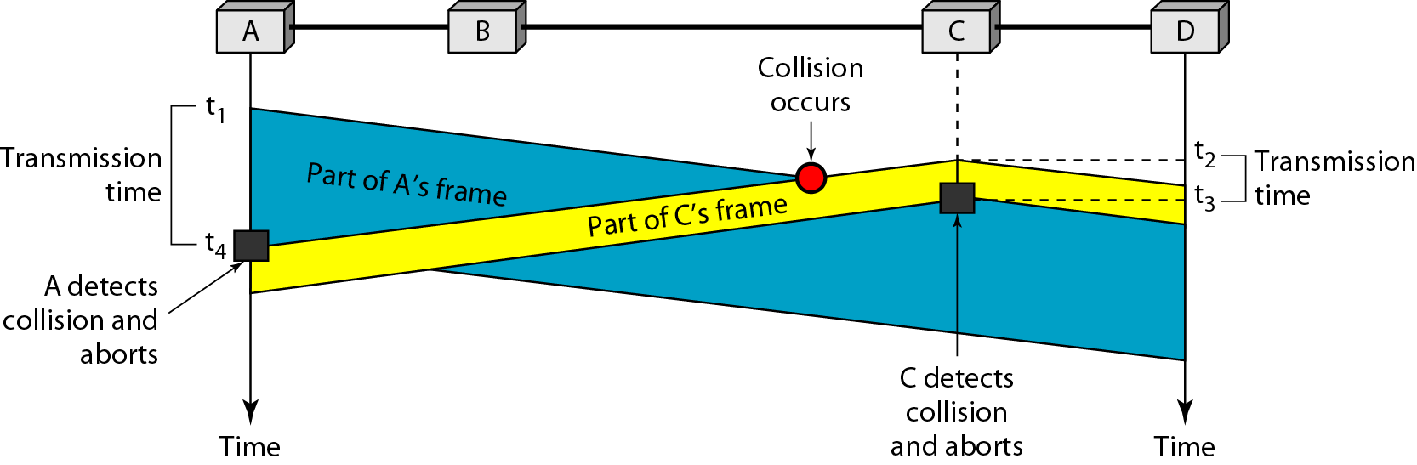
之前CSMA协议中,一个站点只会在发送前进行检查,如果信道空闲就发送

现在CSMA/CD在CSMA的基础上,一个站点会在发送时同时检查,如果侦测到信道中有其他信号,立刻终止发送

因为起码顺着该信号的传播方向上,如果再发送信号肯定是冲突了,那就不如立刻闭嘴不发了

冲突检测时间

首先考虑如图所示情况

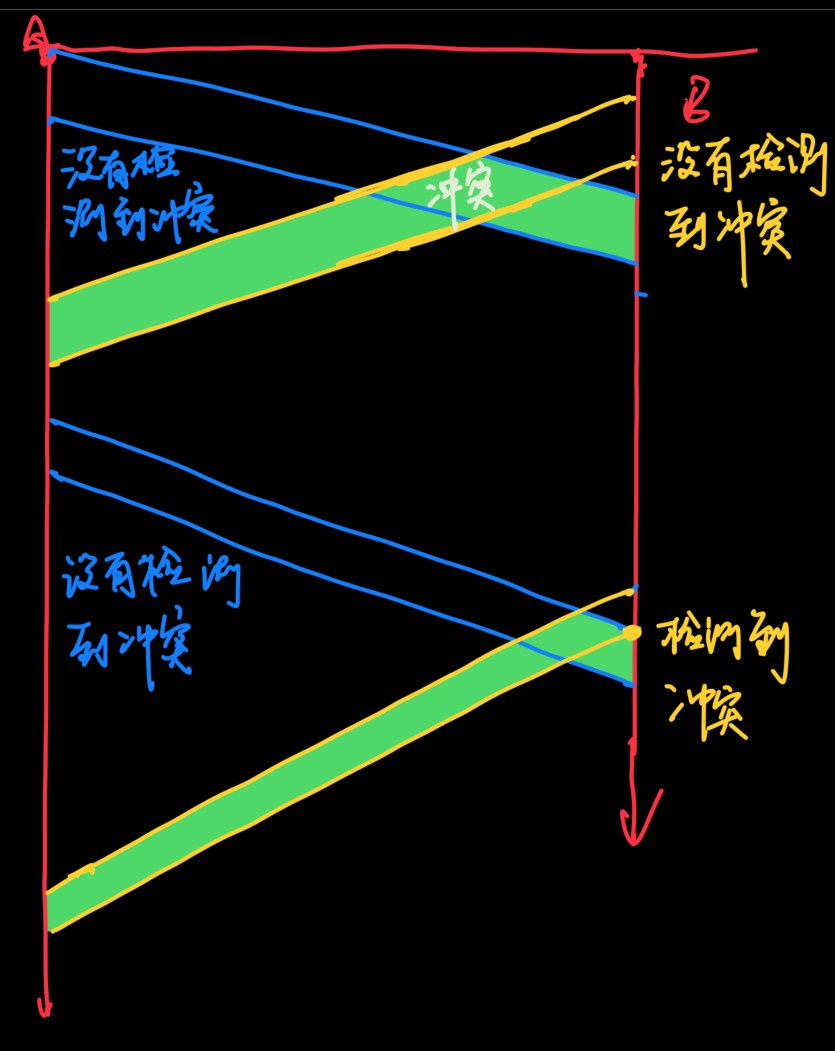
如果传输时间很短但是传播延迟很长,可能就存在双方均检测不到冲突或者只有一方能够检测到冲突的情形

此时冲突废帧会被错误交付

为了避免这种情况,就需要传输时间和传播时间有约束关系

直接考虑距离最远的两个站点A,B的情况即可

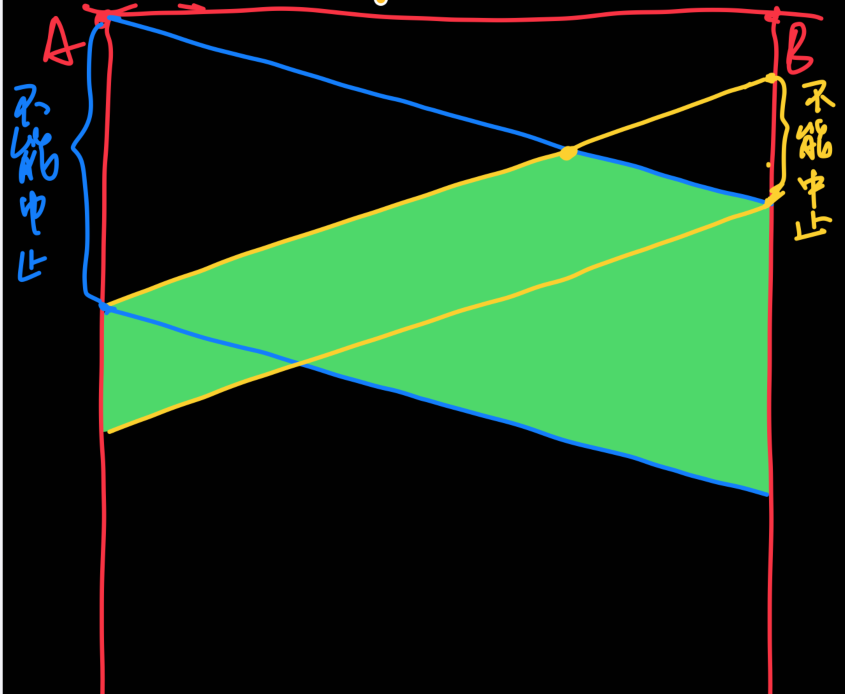
如果B在A的信号马上就要发到时才开始发送,直到B的信号被A侦听到时,A必须仍在发送

也就是说最小传输时间应为最大传播时间的两倍,如下图

因为A,B是两个距离最远的站点,因此是最大传播时间

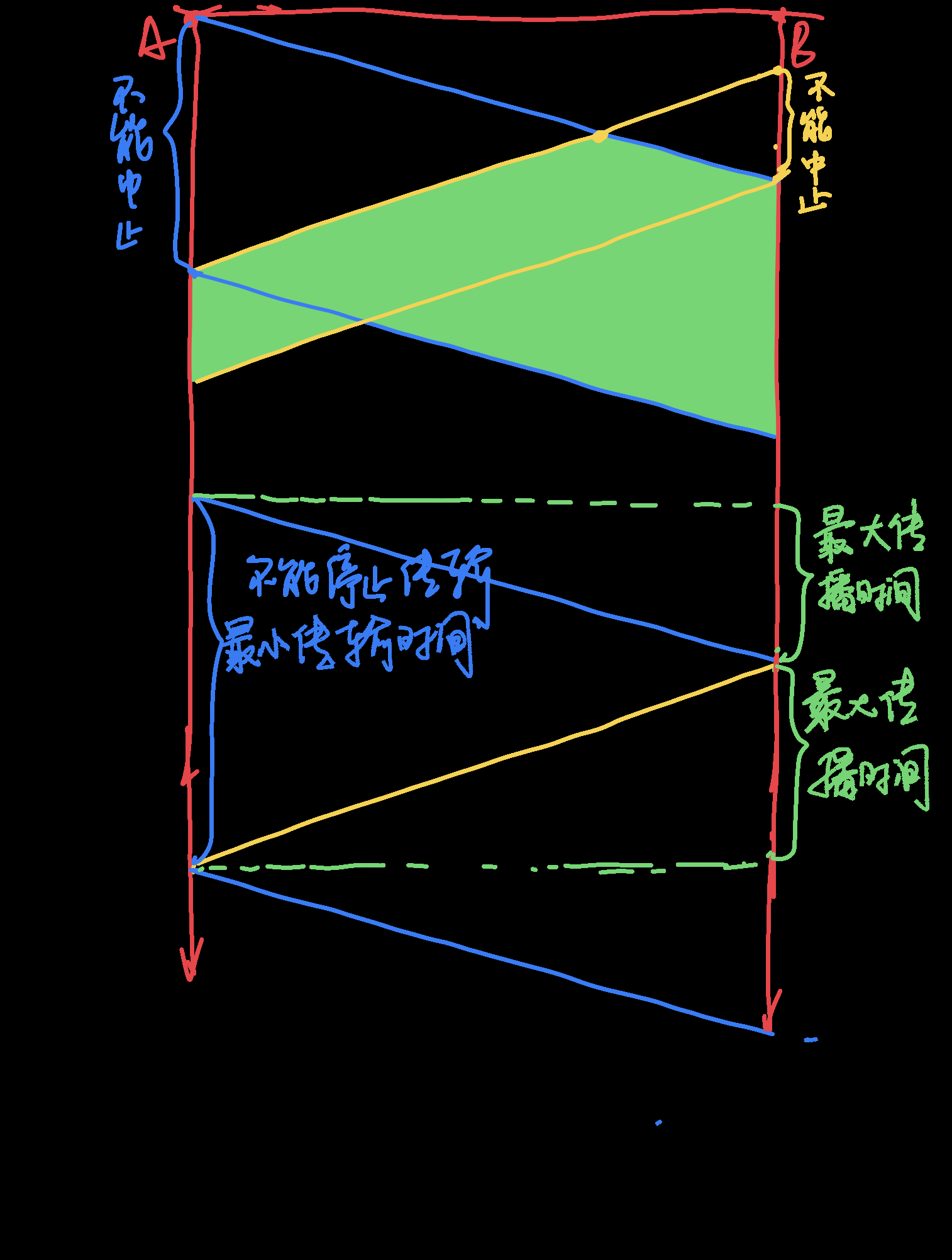
CSMA/CD网络中，带宽10Mbps，最大传播时间为25.6us，那么最小帧长度是多少？

假设帧长是x,则传输时间是$T_{fr}=\frac{x}{10M}$

由$T_{fr}\ge 2T_p$得到 \[ \frac{x}{10\times 10^6}\ge 25.6\times 10^{-6}\times 2 \] 即$x\ge 512bit$

因此帧长最小为512比特

CSMA/CD算法流程

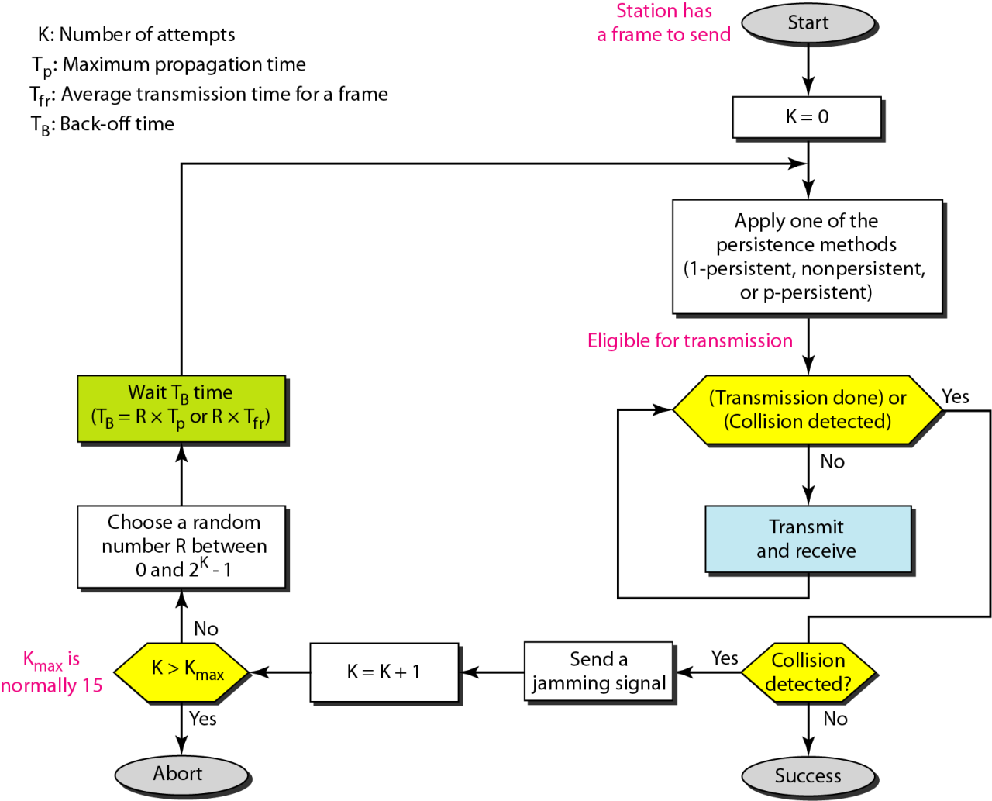
CSMA/CA

Carrier Sense Multiple Access with Collision Avoidance,带冲突避免的载波侦听多路访问

这个协议挺有意思

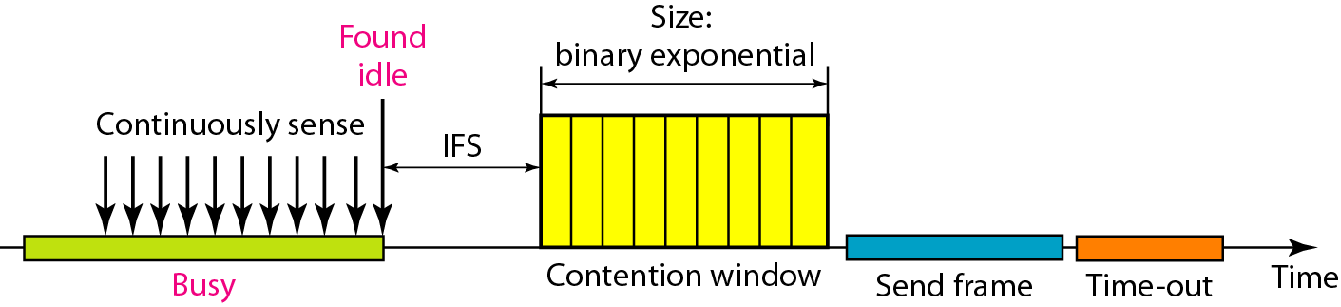
IFS:Interframe Space,IFS 帧间间隔

IFS用于定义一个站点的优先权,优先权高的站点,其IFS就短

为啥IFS短了就意味着优先权高呢?这就需要了解协议如何工作的

Contention Window 竞争窗口

工作流程:

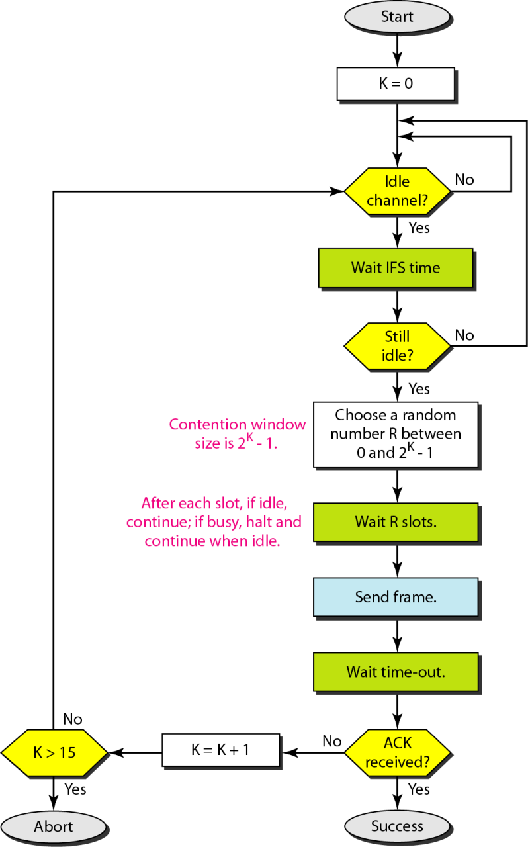
1.首先检查信道是否空闲,如果不是,重新检查

2.如果信道空闲,等待IFS时间

3.等完了再检查一下信道是否空闲,如果忙,退回1.

4.挑一个随机数$R\in[0,2^K)$,也就是在竞争窗口中抓阄

5.等R个时间片,然后检查信道是否忙,如果忙,就等会不忙了再发送.如果不忙就发送

6.发完了设置窗口期等待ACK回复,如果收到,则通信成功,否则K++,回头从1开始,如果K>15则不再尝试,通信事变

以太网

低层协议的组成

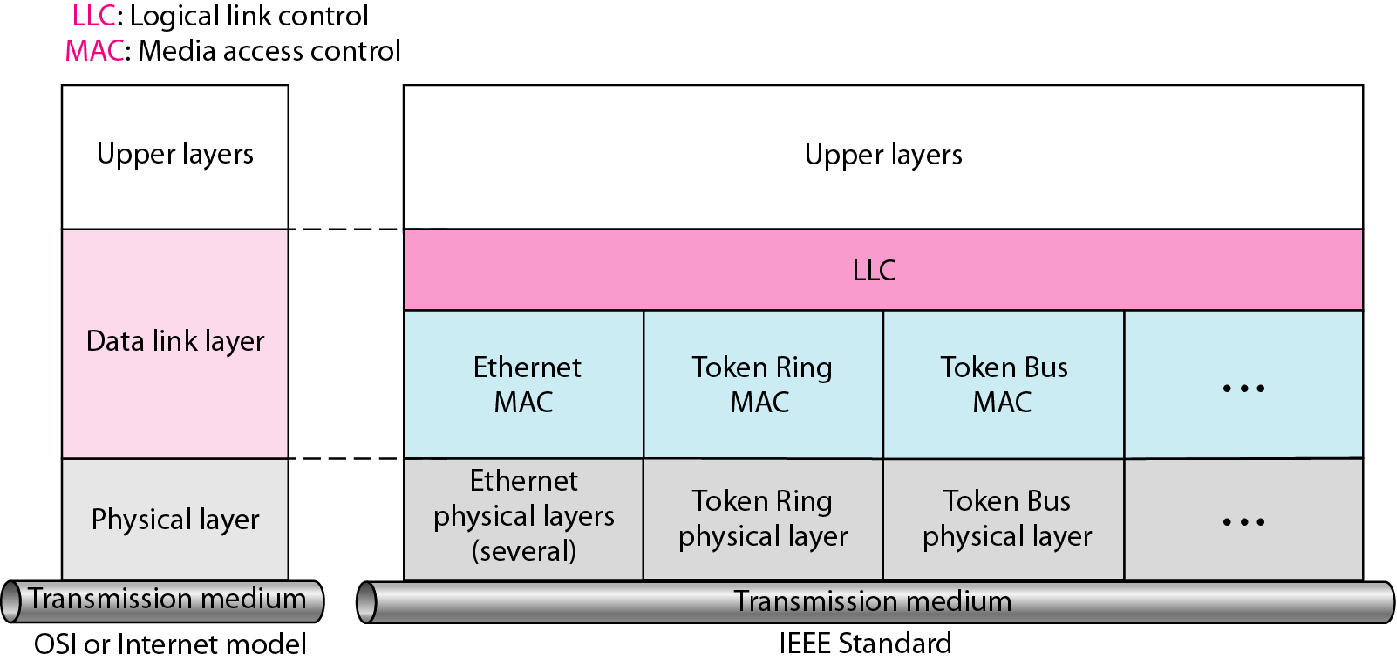
OSI规定的数据链路层分成两个子层,一个是LLC层,一个是MAC层.前者承上后者启下

以太网是MAC的一种实现方式,并且是目前最成功的实现方式

MAC地址

MAC地址规定

以太网地址是一个6字节数,每个网卡都有一个固定的MAC地址

一个计算机可能由多张网卡,因此计算机可以有多个MAC地址

ipconfig /all即可查看

以太网适配器 以太网:

   媒体状态  . . . . . . . . . . . . : 媒体已断开连接
   连接特定的 DNS 后缀 . . . . . . . :
   描述. . . . . . . . . . . . . . . : Realtek PCIe GbE Family Controller
   物理地址. . . . . . . . . . . . . : 84-A9-38-F4-9B-69
...
  
无线局域网适配器 WLAN:

   连接特定的 DNS 后缀 . . . . . . . :
   描述. . . . . . . . . . . . . . . : Intel(R) Wi-Fi 6 AX201 160MHz
   物理地址. . . . . . . . . . . . . : 2C-6D-C1-98-7D-03
....

以2C-6D-C1-98-7D-03为例子,最左边是最高位,

称"第一个字节"为最左边的0x2C,第二个就是0x6D

特殊地址

如果一个MAC地址第一个字节的最低为是0,则该地址是一个单播地址,是1则为多播地址

特殊的,如果MAC addr=FF:FF:FF:FF:FF:FF,则该地址是一个广播地址

0x2C=00101100b,显然所有的物理网卡地址必然是一个单播地址

怎么观察广播地址呢?可以观察ARP协议需要在以太网中广播寻找目标IP地址的主机

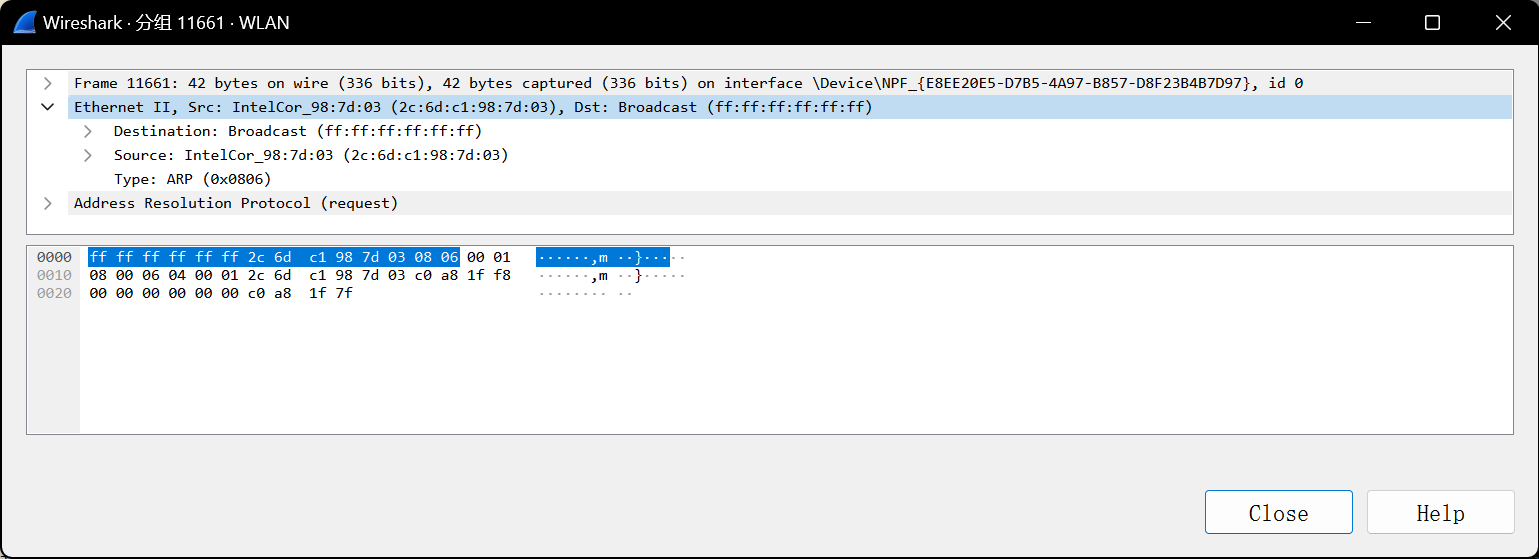
源地址就是本机WLAN网卡的地址2C-6D-C1-98-7D-03,目的地址12个F,显然是一个广播

wireshark已经自动根据本机WLAN网卡的前三个字节判断出本网卡产自Intel公司

再一查好家伙made in 马来西亚

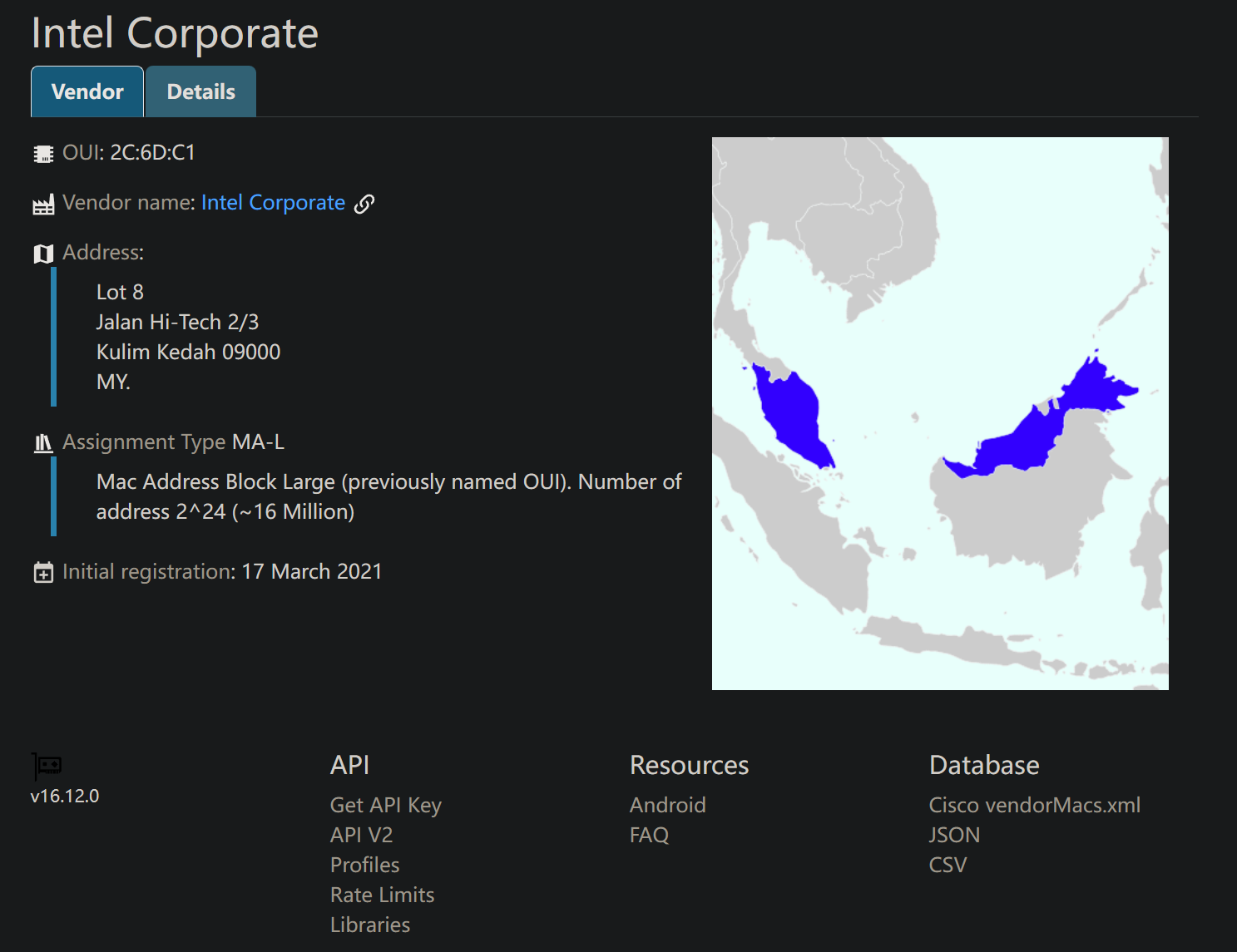
同理华为公司也会买下前三个字节用来标志自己公司的网卡

如果前三个字节是公司编号

那么一个公司编号最多能够产$2^{24}\approx400万$张网卡

如果一部手机使用一个wifi网卡,光中国就有13亿人,假设有1亿人用华为手机,显然一个公司编号是不够用的

网络序

字节序不变,但是每个字节内的比特位分别调转(不是取反,是前后调转)

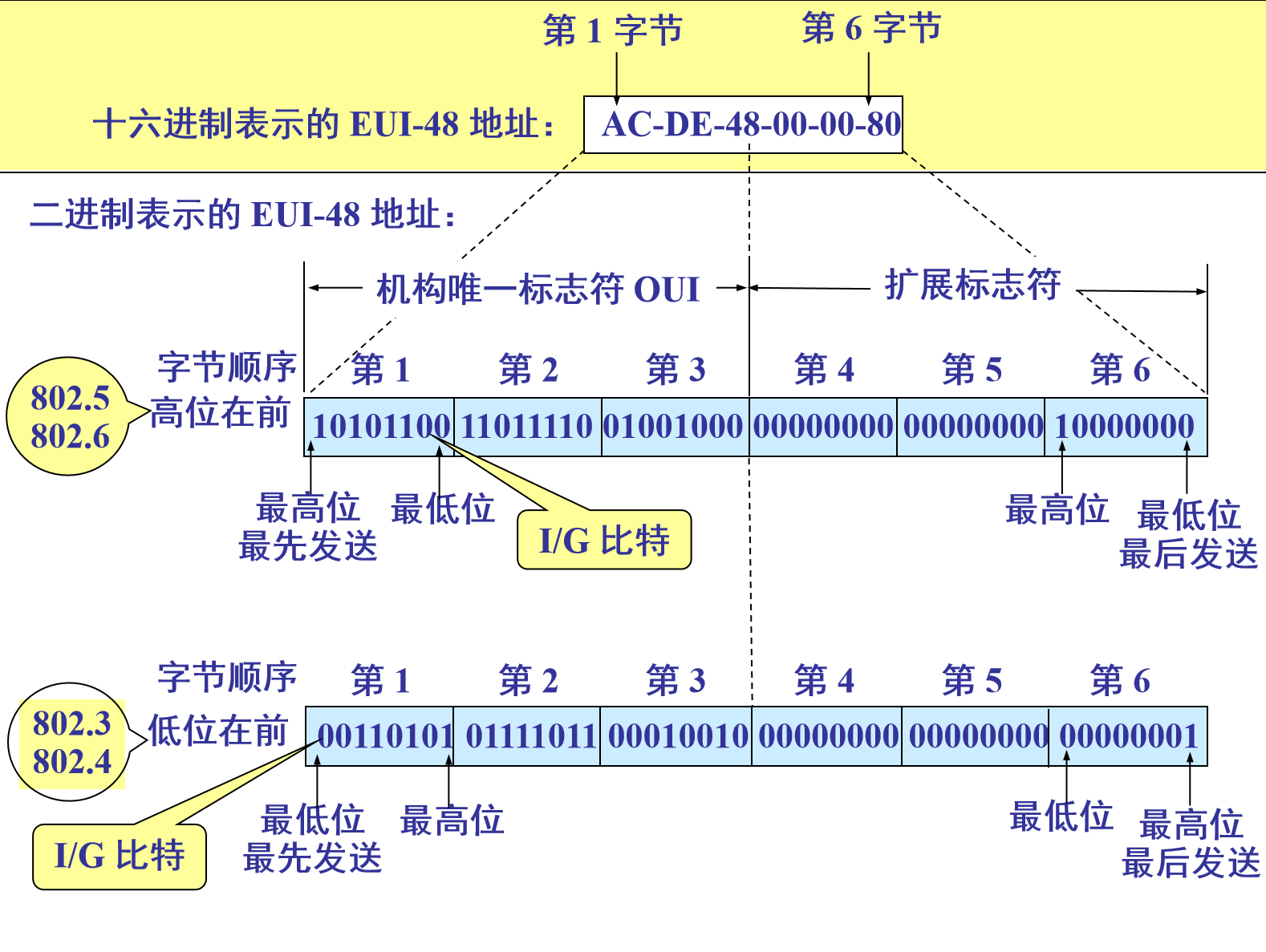
MAC帧格式

MAC帧有两种格式,

不常用的802.2LLC帧,这是IEEE802工作组制定的答辩

最常用的EthernetV2帧

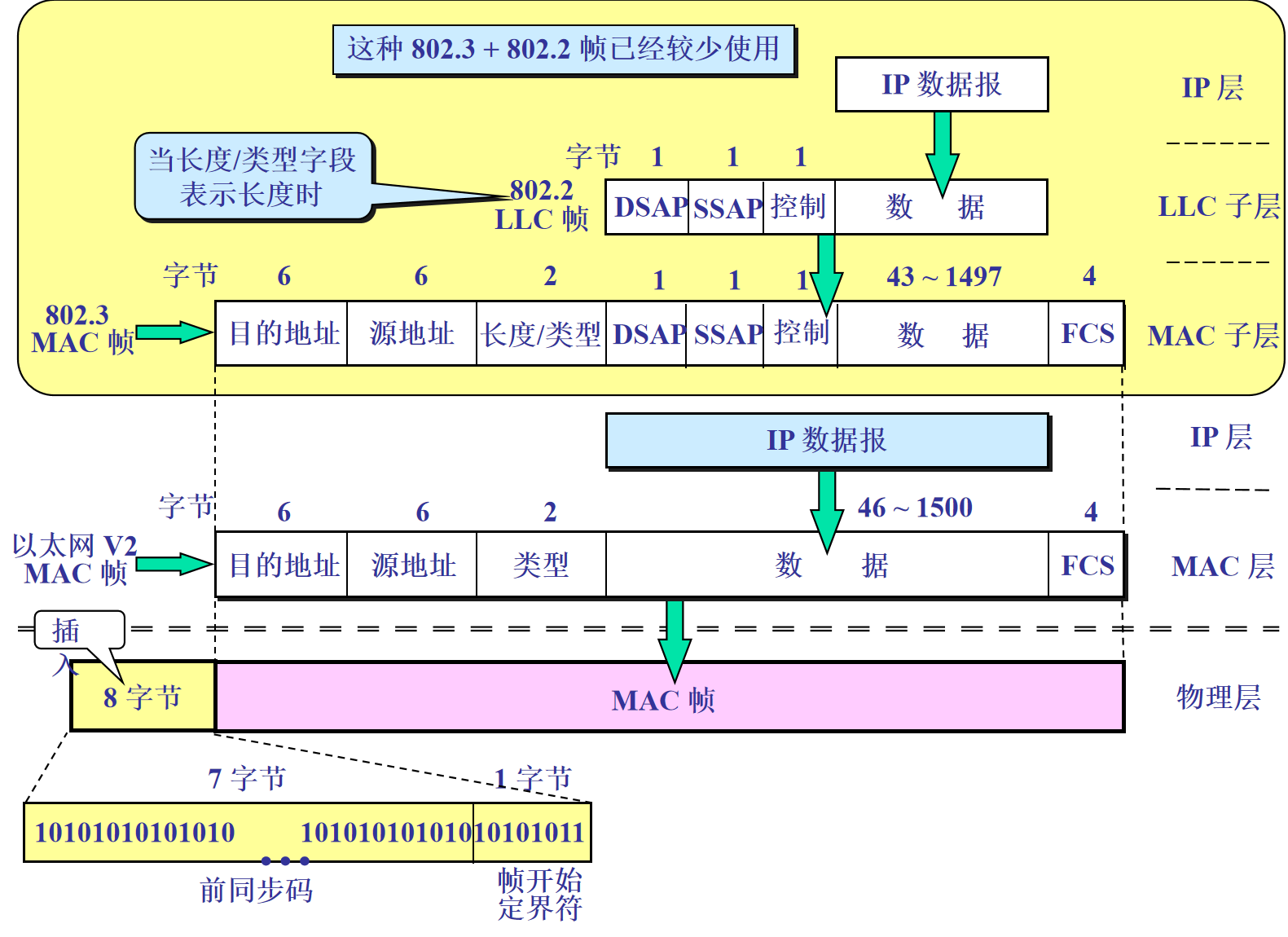
MAC帧=MAC头+MAC数据+FCS

其中MAC头包括目的地址,源地址,MAC数据类型

FCS就是校验和

MAC数据一般是IP数据报,包括IPv4包或者IPv6数据包

不合法的MAC帧

以下有一则为不合法MAC帧

数据字段的长度与长度字段的值不一致；

帧的长度不是整数个字节；

用收到的帧检验序列 FCS 查出有差错；

数据字段的长度不在 46 ~ 1500 字节之间；

MAC 帧长度不在64 ~ 1518 字节之间；

对于检查出的无效 MAC 帧就简单地丢弃，以太网不负责重传丢弃的帧。

这里对帧长度有一个规定,[64,1518]为啥会有这两头的限制呢?

合法帧长度

[64,1518]bytes

由于有限以太网使用CSMA/CD协议,因此需要保证最小传输时间大于等于两倍的最大传播时间

而这两个时间的关系,关乎帧长度啥事呢?

显然帧长越长,传输时间就越长,可以推测帧长为64bytes时达到临界值

根据802.3规定,以太网最长2500米,带宽10Mbps,四个中继器,最坏情况下,往返时间(也就是两倍的最长传播时间)大约是50μs.

那么传输速度应该大于50μs.

又带宽是10Mbps,在50微妙内能够发送$50\times 10^{-6}s\times 10\times 10^6bps=500bit$

增加安全边际,往上取整到512bit=64byte

因此规定最小帧长就是64byte

那么又为啥限制最长帧长为1500呢?

因为网络是多台计算机共享的,如果一台主机一直喋喋不休地说,其他主机就得等着,因此一句话不能说太长

于是人为规定为最长1518byte

那么在以太网上的IP包长度就跟着被限制到[48,1500]字节

这个1500字节也就是MTU,最大传输单元

网络连接

数据链路层设备

网桥,集线器,二层交换机都是链路层设备

一层设备	结构	作用
中继器		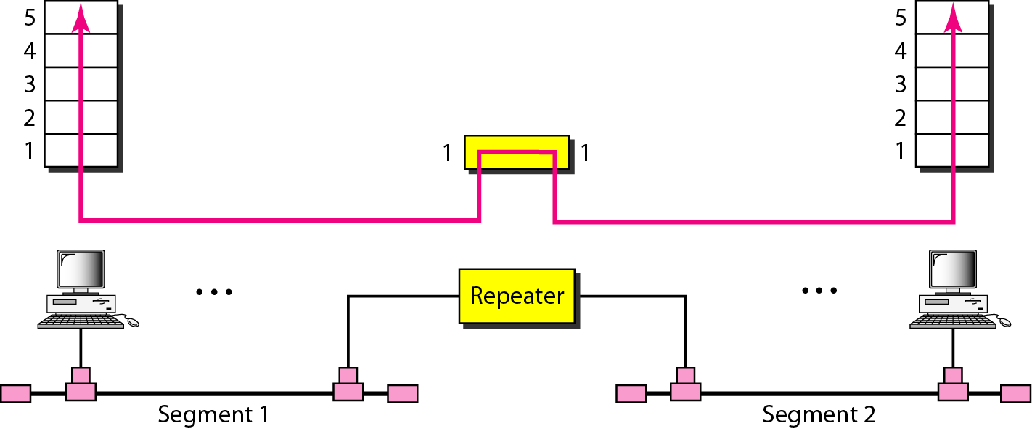再生信号(不是放大信号),延长通信距离
集线器	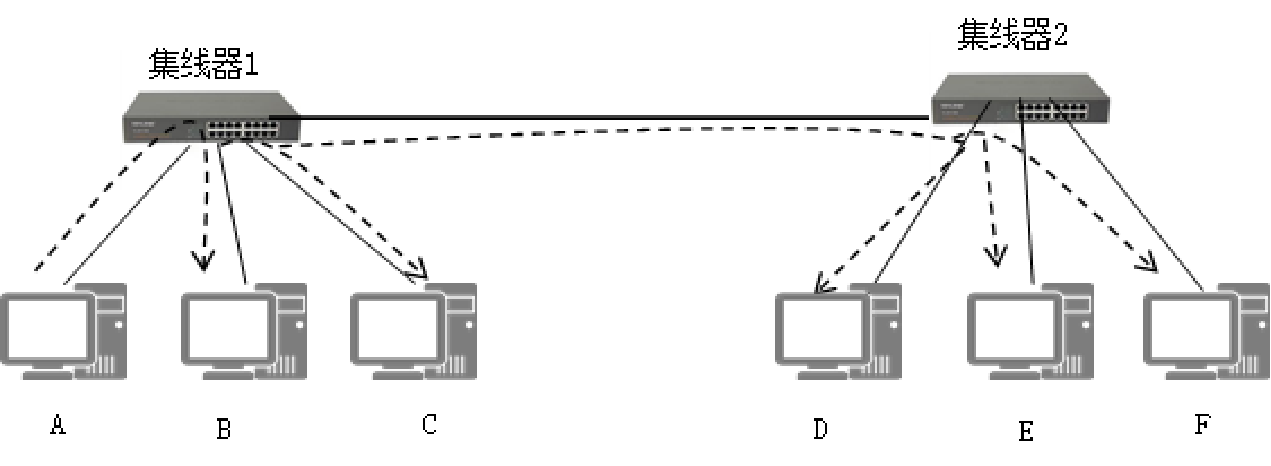所有计算机同处于一个冲突域集线器从一个端口进来的包会被无脑拷贝到所有的出端口	只是把多个主机联通, 相当于多通水管多端口的中继器

二层设备	结构	作用
网桥	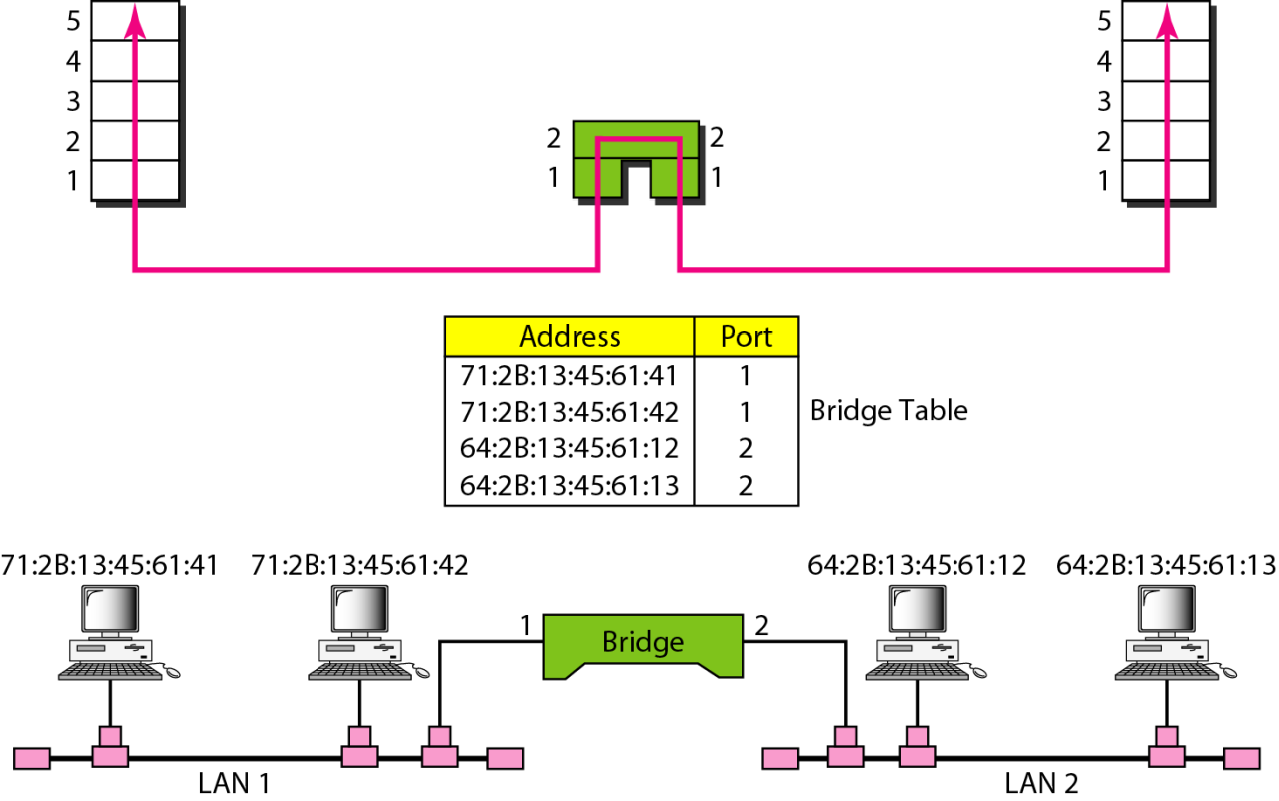网桥可以检查目标地址,根据自己学习建立的转发表,决定从哪个端口转发,相对集线器聪明了不少	减小冲突域,网桥的一个接口是一个冲突域但是所有达到接口都在同一个广播域
二层交换机		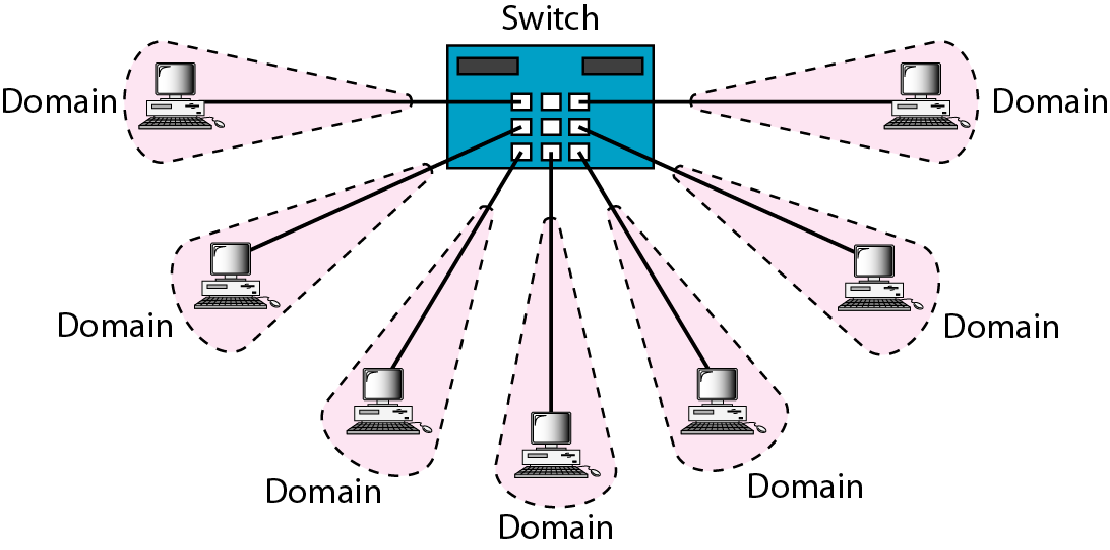消除冲突域,从此不再有冲突相当于带阀门的多通水管但是所有接口都在同一广播域

区分两个术语:广播域,冲突域

广播域:能够接收广播帧的所有设备的集合

冲突域:所有共享介质(比如电缆)都是冲突域

显然广播域的范围要大于等于冲突域

以太网:有线局域网的一种实现,链路层使用CSMA/CD技术

网桥

爱学习の网桥

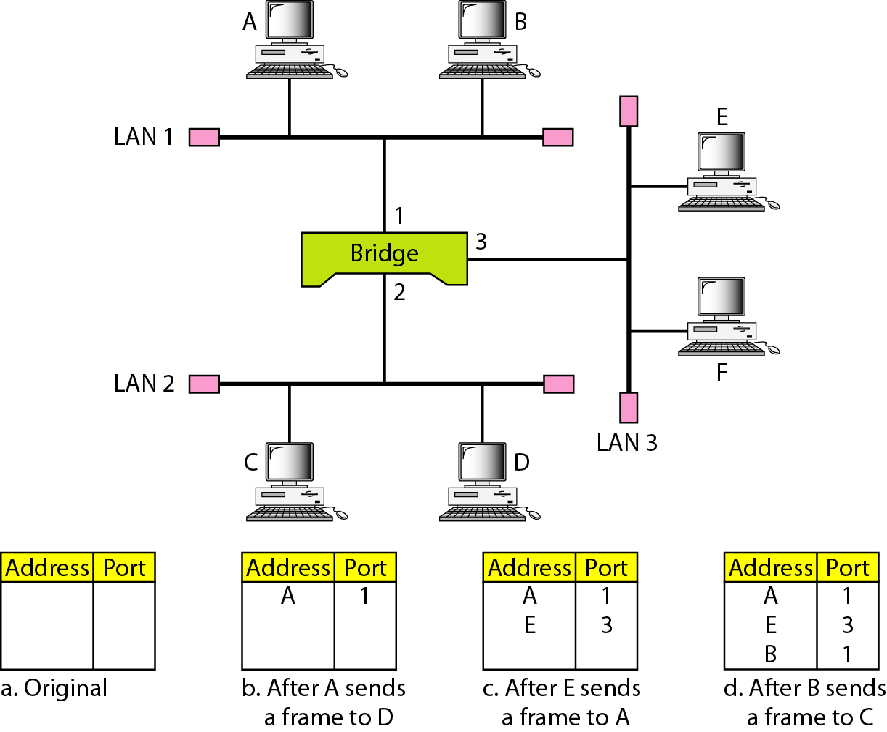
刚接入局域网的网桥是个傻子,啥也不知道,但是他很快就会知道

一开始他的MAC:Port映射表是空的

当A@LAN1 向 D@LAN2发送一个数据帧之后,这个帧显然必须从网桥的1号端口进入.网桥从帧中得知,源地址A在1端口对应的LAN上,于是将A:1写入映射表

如果D回复A收到,立刻就会把D的MAC暴露给网桥,网桥就会记录D:2

D不回复也没关系,反正D只要一说话立刻就会被网桥学会

环路问题

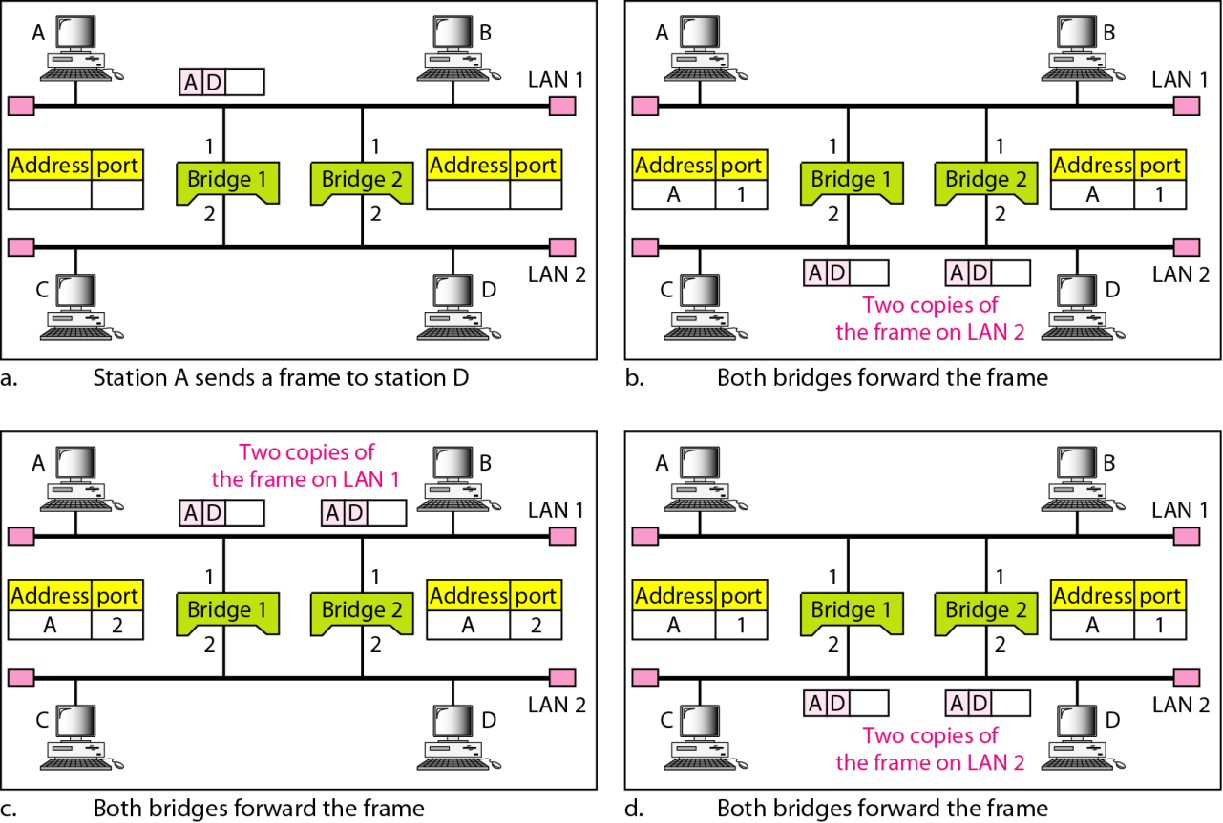
如果有两个网桥同时连接了两个LAN

那么一个LAN发出的帧会同时被两个网桥转发,导致另一个LAN中出现两次该帧

生成树算法

生成树算法用于建立多个LAN的最优联通路径

这里的最优可能是最小跳数,最小延迟,最大带宽等等

假设从网桥到LAN跳数为1，从LAN到网桥跳数为0。

为啥要这样假设呢?

因为网桥不会主动向一个LAN发送帧,除非该帧的目的在这个LAN中

而一个LAN的帧要想传送到另一个LAN,必须要经过网桥

也就是说,网桥转发帧需要一定的代价,应该尽量减少转发量

而LAN向网桥发送帧这是不可阻阻挡的,几乎没有代价

因此有这么一个假设

首先将网桥和LAN进行有向图建模,并标注边权

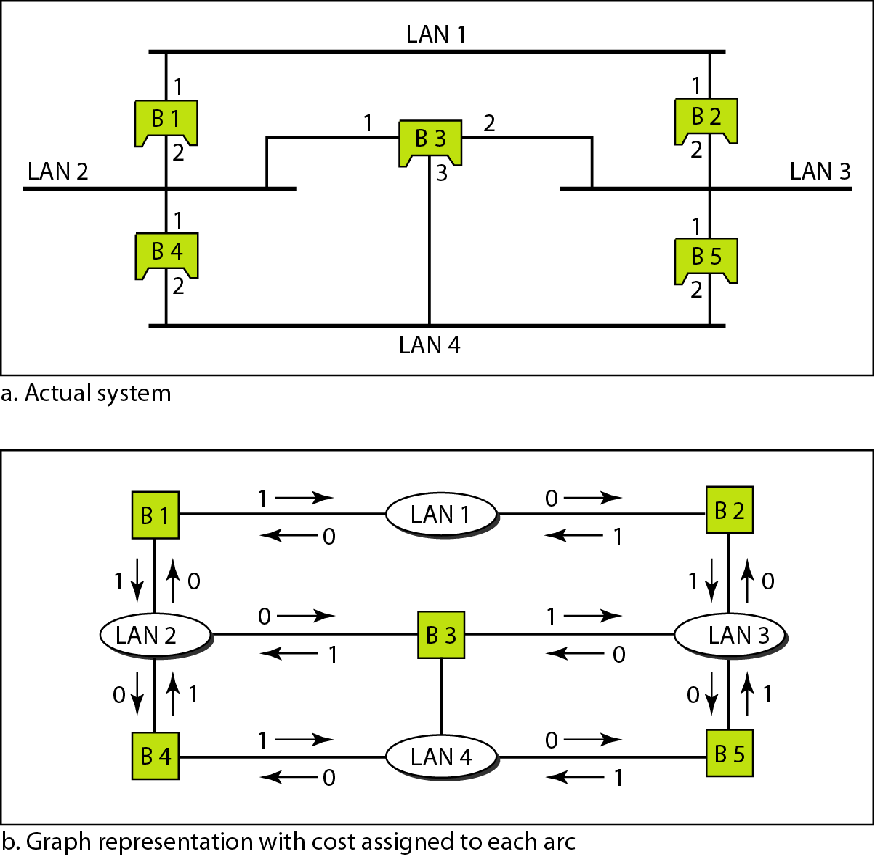
为啥没有两个网桥直接连接?或者两个LAN直接连接?

这不废话吗

两个网桥连接和只用一个网桥不一样吗?

两个LAN连接就是一个LAN

两个LAN连接也得使用网桥啊(

生成树算法:

spanning tree algorithm:

1.每个网桥广播ID,选择最小的ID作为根网桥

2.找出从根网桥到其它网桥或LAN的最短路径

3.最短路径组合生成最短的树

4.标记转发端口和阻塞端口

注意生成树算法目的是,找出从根网桥到其他网桥和LAN的最短路,

而不是为每个LAN找出到其他各个LAN的最短路

使用生成树算法之后,阻塞端口不再使用,转发端口活跃

交换机

交换机相对于集线器的优点:

1.每个端口是一个冲突域

2.根据目标MAC地址查转发表,决定发往哪个端口

3.全双工,由于没有冲突域,不需要CSMA/CD协议

4.有缓存,各个接口的带宽可以不同

网络层设备

链路层设备关心帧的MAC地址

网络层设备关心包的IP地址

三层设备就一个三层交换机和一个路由器

这个三层交换机不伦不类,它既有二层交换机那个交换转发的功能,也有路由器的路由功能

两者本身上的区别是,三层交换机主要是硬件驱动的,但是路由器是CPU+操作系统软件驱动的.这就导致三层交换机的效率远快于路由器

两者功能上的区别是,三层交换机用于连接相同性质的网络,比如连接两个LAN:192.168.2.1/24和192.168.1.1/24

但是路由器主要用于不同类型的网络连接,比如因特网和局域网的连接,入户网线可能给一个互联网的公网地址,需要使用一个路由器NAT转化为一个LAN.并且实际上的路由选择,负荷分担,链路备份,和其他网络交换路由信息,都是路由器实现的

路由功能:当IP报文抵达路由器时,决定转发给哪一个下一跳路由器

这个决策是基于路由器的路由表做出的

路由表可以人工填写静态的,也可以让路由器自己学,就跟网桥交换机的转发表差不多

网关

比较特殊的路由器

一个LAN内的主机如果想要跨LAN访问另一个主机,只通过二层交换机是做不到的,因为二层交换机是连IP地址都不知道的傻子.网关就是一个LAN和外部网络连接的关口.LAN内的主机只要是想和外部通信,无脑往网关发包就可以了,网关负责决定这个包如何路由

虚拟局域网

交换机可以隔离冲突域但是无法隔离广播域

划分虚拟局域网之后可以隔离冲突域和广播域

在一个交换机上划分了VLAN,实际上相当于虚拟出多个交换机,每个交换机都分别连接到路由器上,形成多个LAN,并且这几个LAN互不连通.这个路由器就是各个LAN的网关

等效结构

如图所示

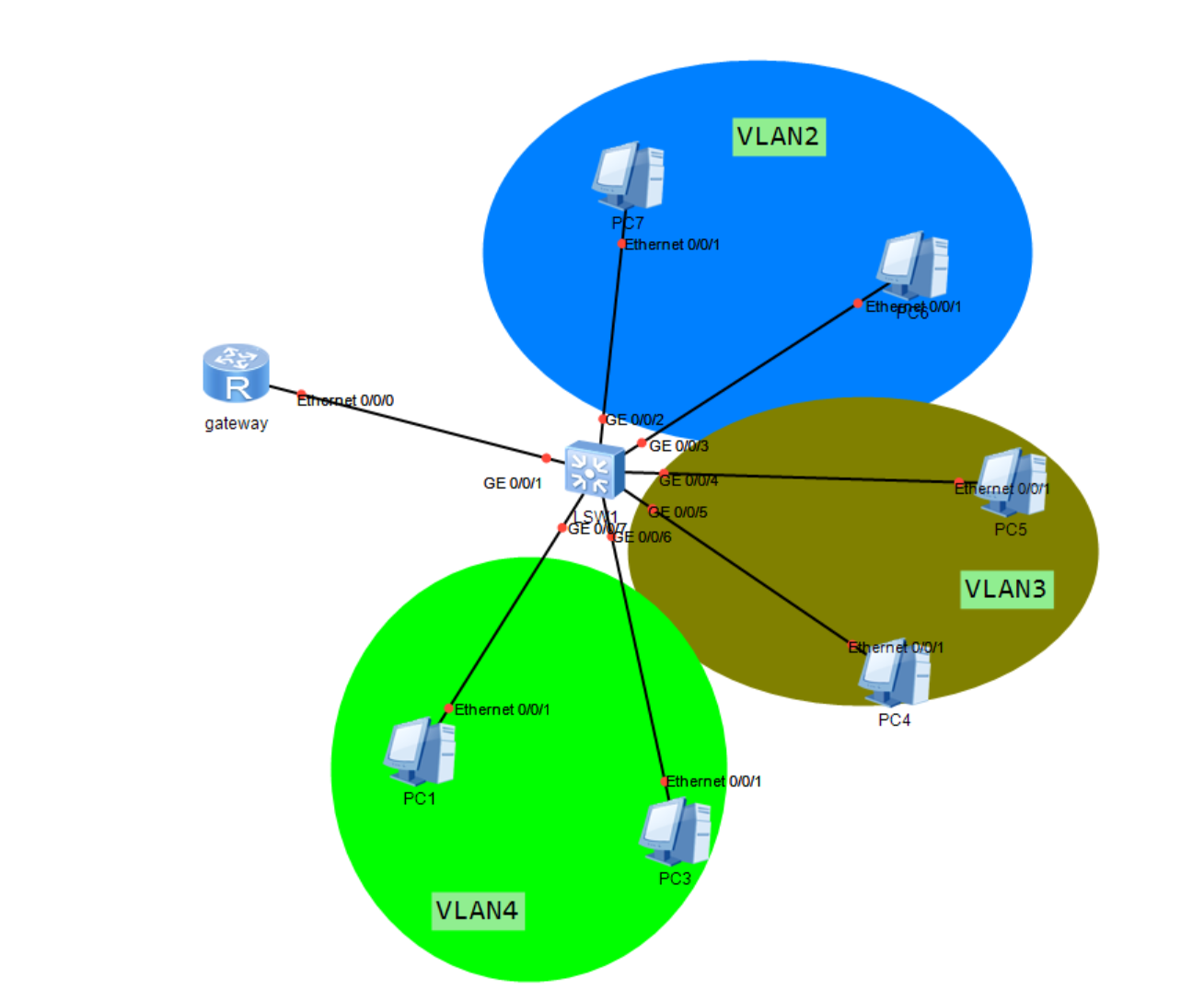
这实际上就相当于

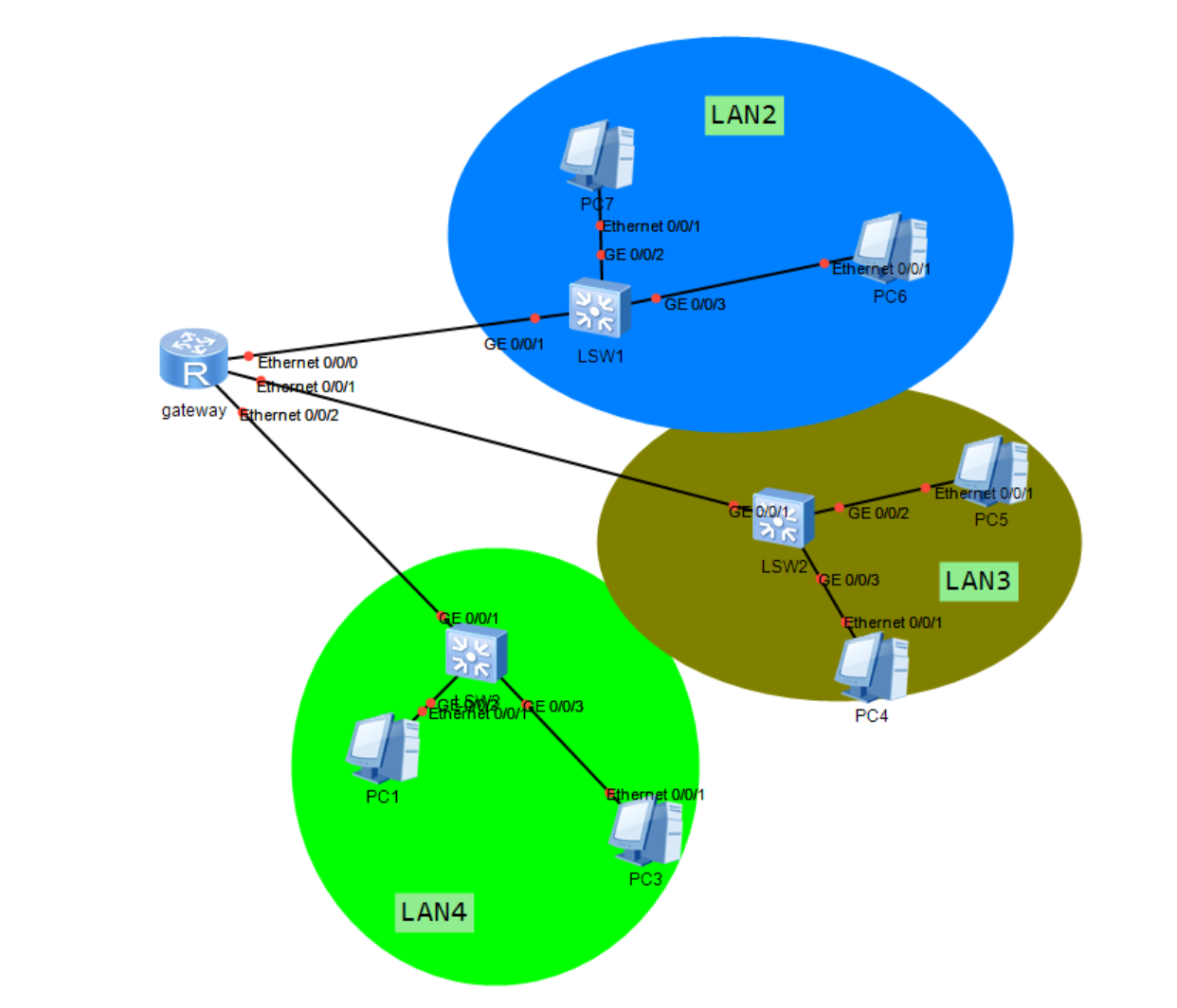
如何实现

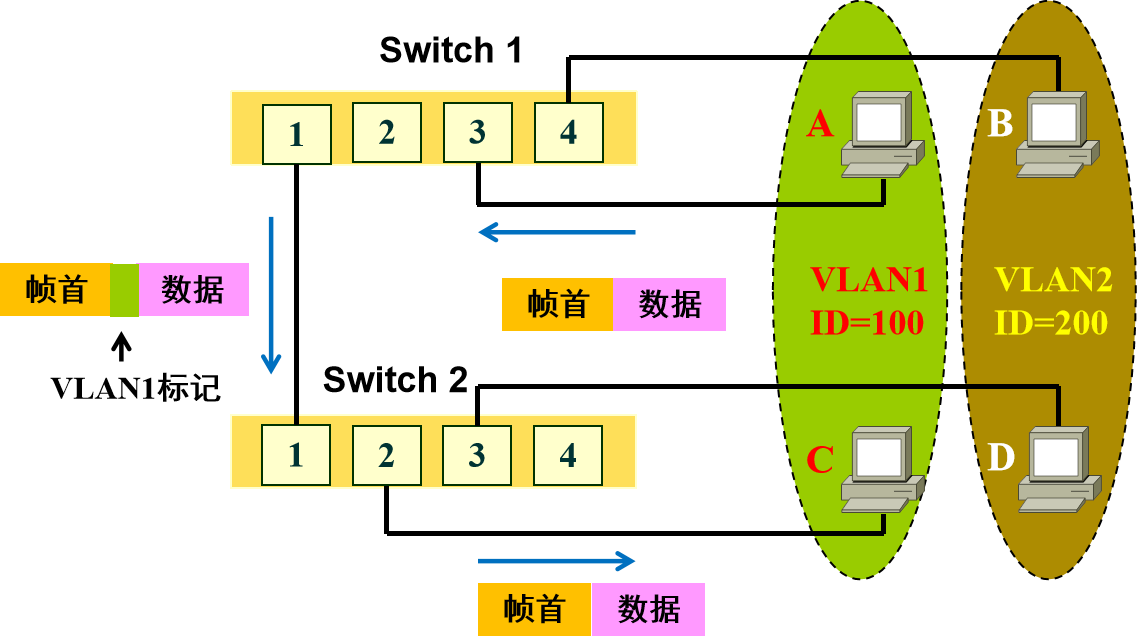
如果一个VLAN跨越了两个交换机,那么这个VLAN中两个计算机通过交换机通信时,交换机在发往另一个交换机之前,检查A计算机所处VLAN,然后在链路层帧后面加上VLAN标志,这样另一个交换机就知道把改帧转发给哪一个目标VLAN了

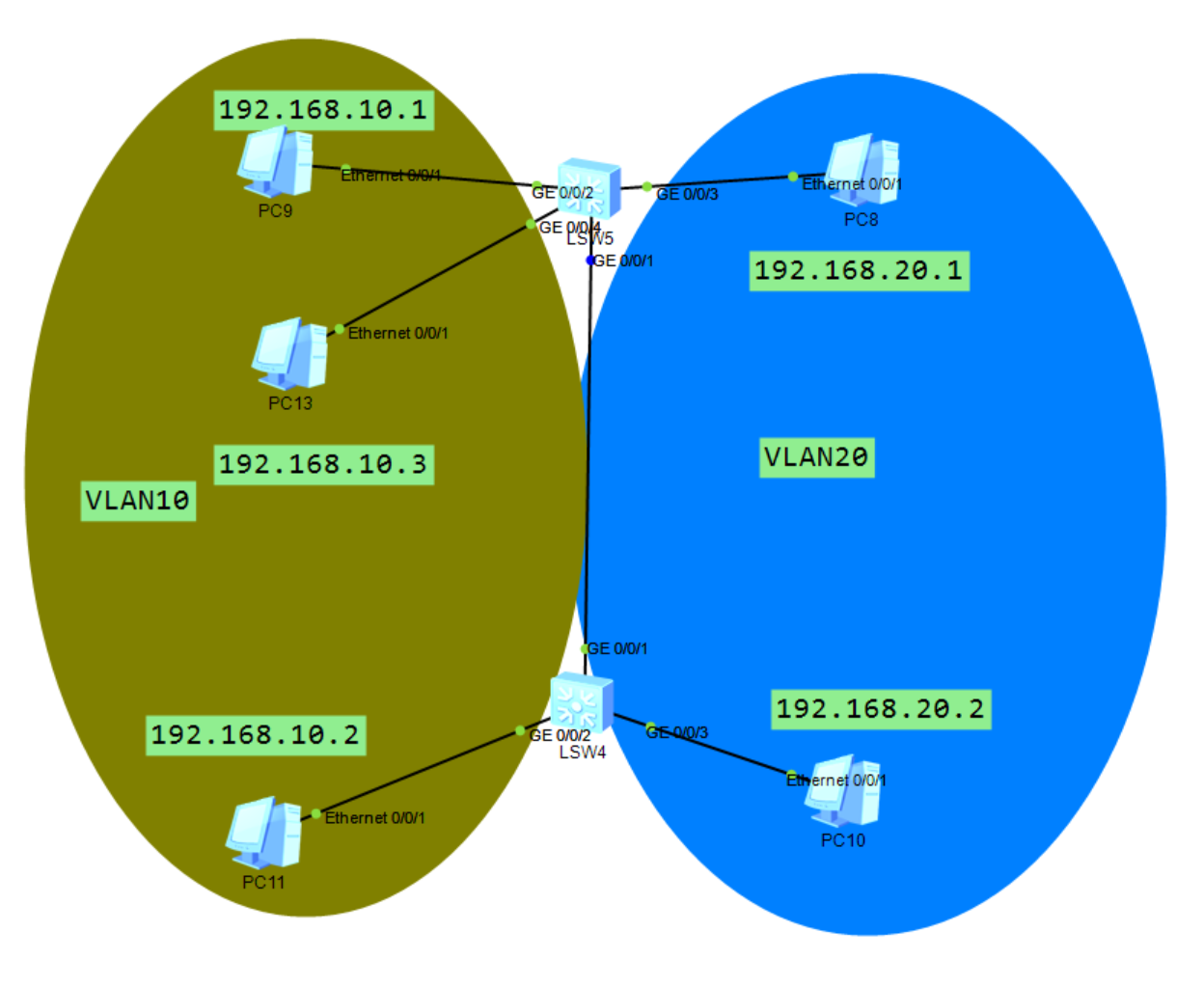
如图所示的拓扑中,经过实验,PC9@192.168.10.1 ping PC13@192.168.10.3时,ICMP报文会被LSW5交换机准确地从GE0/0/4口转发到GE0/0/2端口,报文中也没有体现VLAN

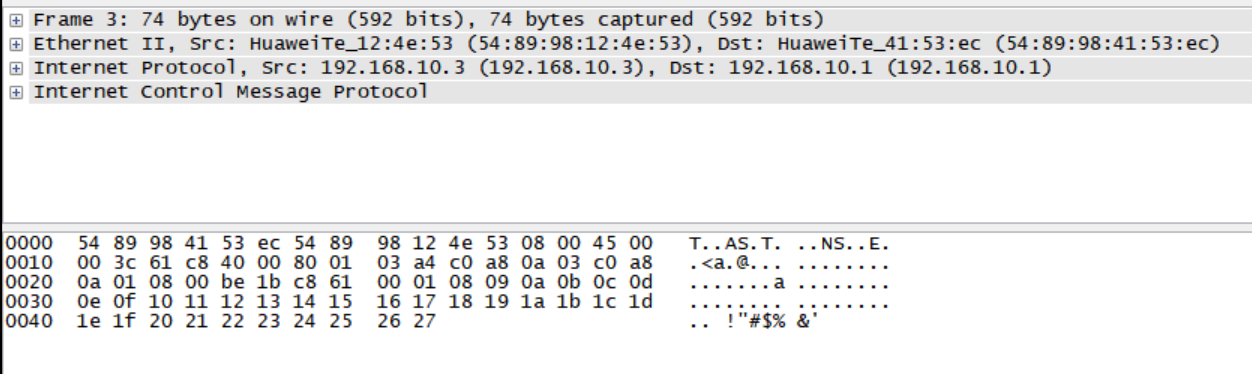
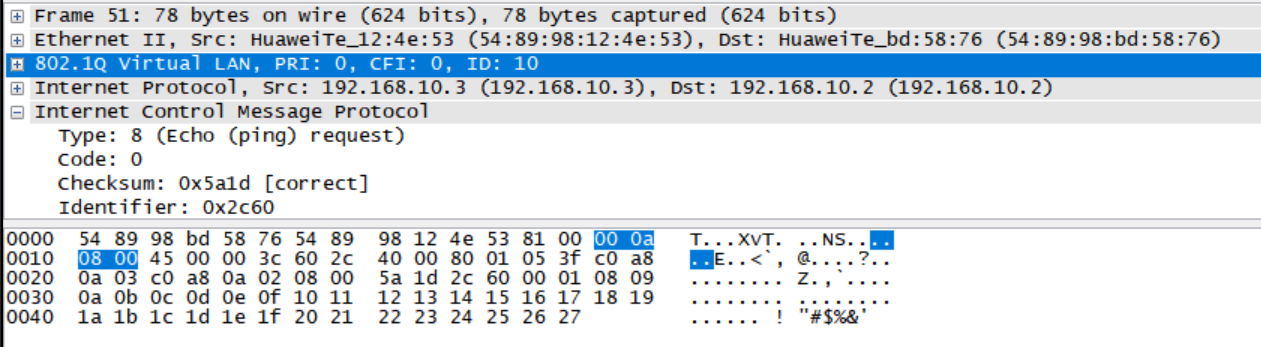
PC13@192.168.10.3 ping PC11@192.168.10.2时会经过两个路由器的Trunk端口,其报文中,以太网头和IP头之间加上了VLAN编号,占用四个字节,这个玩意叫做tag(标签)

交换机端口类型

access类型,只属于一个VLAN,用于连接计算机

trunk类型,主干道,可以设置允许哪些VLAN通过,用于连接交换机

hybrid类型,类似于trunk,但是hybrid允许通过改接口的帧不带VLAN tag,而trunk要求必须带VLAN tag(除了缺省VLAN,默认是VLAN 1,的帧不需要带tag)

当端口接收到不带VLAN Tag的报文后，则将报文转发到属于缺省VLAN的端口(如果设置了端口的缺省VLAN ID,默认是VLAN 1)。

当端口发送带有VLAN Tag的报文时，如果该报文的VLAN ID与端口缺省的VLAN ID相同，则系统将去掉报文的VLAN Tag，然后再发送该报文。