计算机网络-物理层

物理层

比特率:一秒内发送的位数,bps,b/s

比特长度=传播速度*传播时间,即一个比特在传输介质上的距离

复合信号:简单正弦信号的叠加信号

带宽:符合信号的组成成分中,最高频率与最低频率的差

模拟信号:用连续变化的物理量表示信息

数字信号:用离散的物理量表示信息

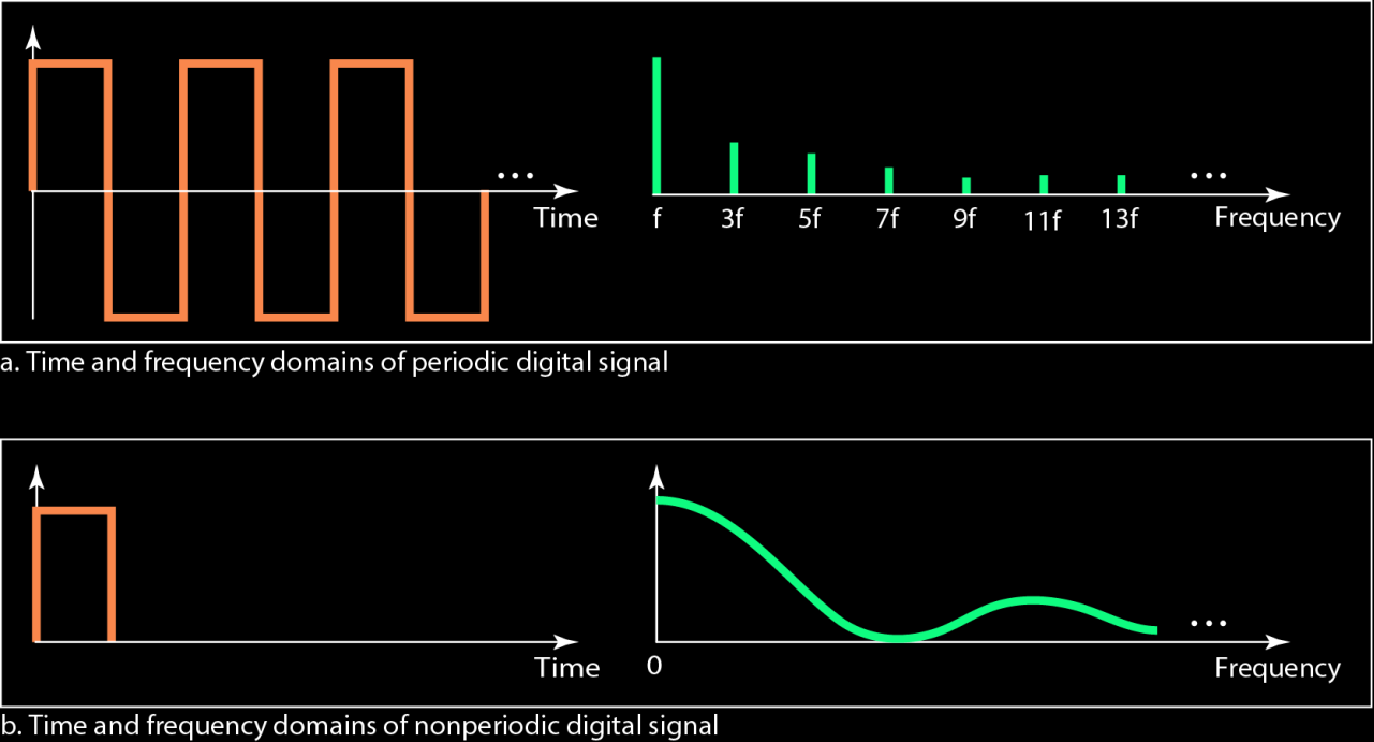
模拟信号和数字信号的关系

实际上数字信号是带宽无穷大的复合的模拟信号

至于为啥非周期性的数字信号,其频率是连续的,而周期性的数字信号,其频率是离散的呢?

也就是说,为什么周期性的数字信号做傅里叶变换之后,在频域得到的是频率离散的正弦波呢?

首先证明,离散的正弦波叠加一定能够得到周期性复合波形

直接取这些正弦波周期的最小公倍数,一定是该复合波形的周期

对于$f(x)=Asin(\omega x+\phi)$设T为其周期,则有$f(x+T)=f(x)$

不妨设这些正弦波的最小公倍数为nT

那么 \[ f(x+nT)=f((x+(n-1)T)+T)=f(x+(n-1)T)=...=f(x) \] 对于$F(x)=\sum_{i=0}^n A_isin(\omega_ix+\phi_i)=\sum_{i=0}^n f(x)$

自然有$F(x+nT)=F(x)$

然后证明,连续频率的正弦波叠加,无法形成周期性信号

假设$f(x)=Asin(\omega x+\phi)$,其中$\omega$在$[a,b]$上连续

则 \[ F(x)=\int_{a}^bA(\omega) sin(\omega x+\phi(\omega)) d\omega \] 即证明$F(x)$不是周期函数

假设$F(x)$是周期函数,设T为其一个周期,则有F(0)=F(T),那么就得有 \[ \int_{a}^bA(\omega) sin(\phi(\omega)) d\omega=\int_{a}^bA(\omega) sin(\omega T+\phi(\omega)) d\omega \]

即 \[ \int_{a}^b A(\omega)[sin(\phi(\omega)) - sin(\omega T+\phi(\omega))] d\omega=0 \] 其中 \[ sin(\phi(\omega)) - sin(\omega T+\phi(\omega))=2cos\frac{2\phi(\omega)+wT}{2}sin\frac{-\omega T}{2} \] 然而这个式子无法证明成立,倒是可以举反例证明不成立,比如令A=1,$\phi=0$

则$-\int_{a}^b sin\omega \ d\omega=0$显然不正确,因为a,b可能不够一个周期

为什么说数字信号是带宽无穷大的复合模拟信号?

先说为啥数字信号是一个模拟信号

根据傅里叶变换,非周期数字信号是连续频率的正弦波的叠加

周期数字信号是离散频率的正弦波的叠加

这个频率的上下界是多少?下界是0,上界是无穷大,为啥是无穷大?

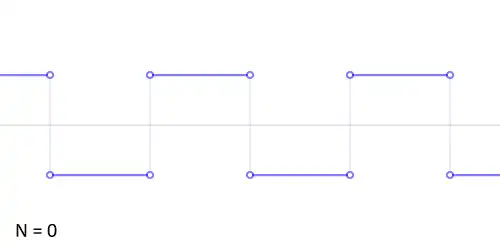
N越大,也就是谐波越多,波形越接近方波,拐弯的时候越接近直角

当N趋向无穷大时,才可以认为波形是方波

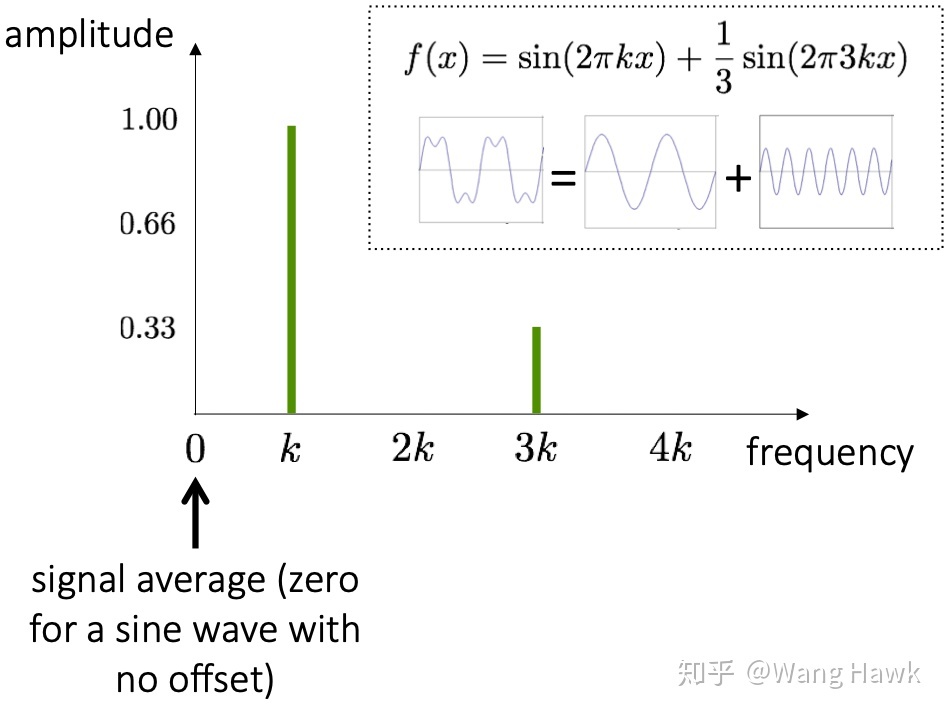
振幅体现成什么?

在频域图上观察更加明显

振幅越大的分量,代表这个分量信号在复合信号中的影响更大.

可以这样理解:

三个人一起说话,我们从远处只能听见说话声音大的那个一,几乎听不到其他人说话,但是实际上我们听到的是三人声音的复合信号,只不过另外两个人的劲太小,发出的信号振幅小,能量小,我们听不清

传输方式

基带传输

直接传输数字信号,要求该信号的最低频率成分,其频率是0.

理想情况下,传递1101110这么一串信息,可能就是高高低高高高低电平的变换.

但是实际上由于基带传输需要无穷大的带宽,而实际的信道带宽有限

这就意味着,要噶掉一些频率过高或者过低的谐波.

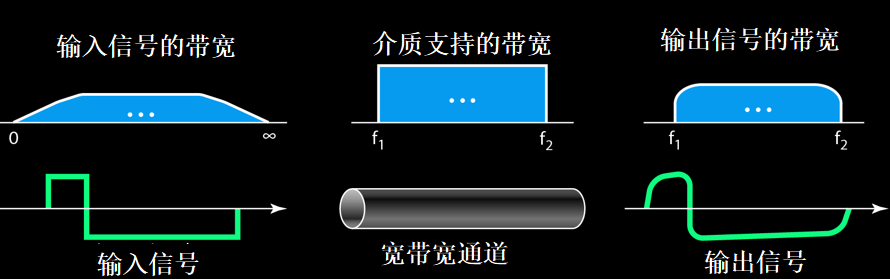
这就会造成波形失真

为什么噶掉一些谐波就会造成波形失真?

还是这个图,如果只保留N=1,也就是噶掉了其他所有频率的分量,那么图像就是只一个正弦波,根本看不出方波了

如果被噶掉的部分,有些频率的分量,其振幅很大,也就是在符合信号中的话语权比较重,那么被噶掉之后,波形失真就会很厉害

这就好比一场音乐会,去掉一些和声,普通人可能也察觉不出来

但是去掉劲最大的主唱,傻子也能听出来,怎么开始放伴奏了?

但是只要能够保持波形的大概就可以了,接收方会复原信号

因此使用有限频率的分量就可以了

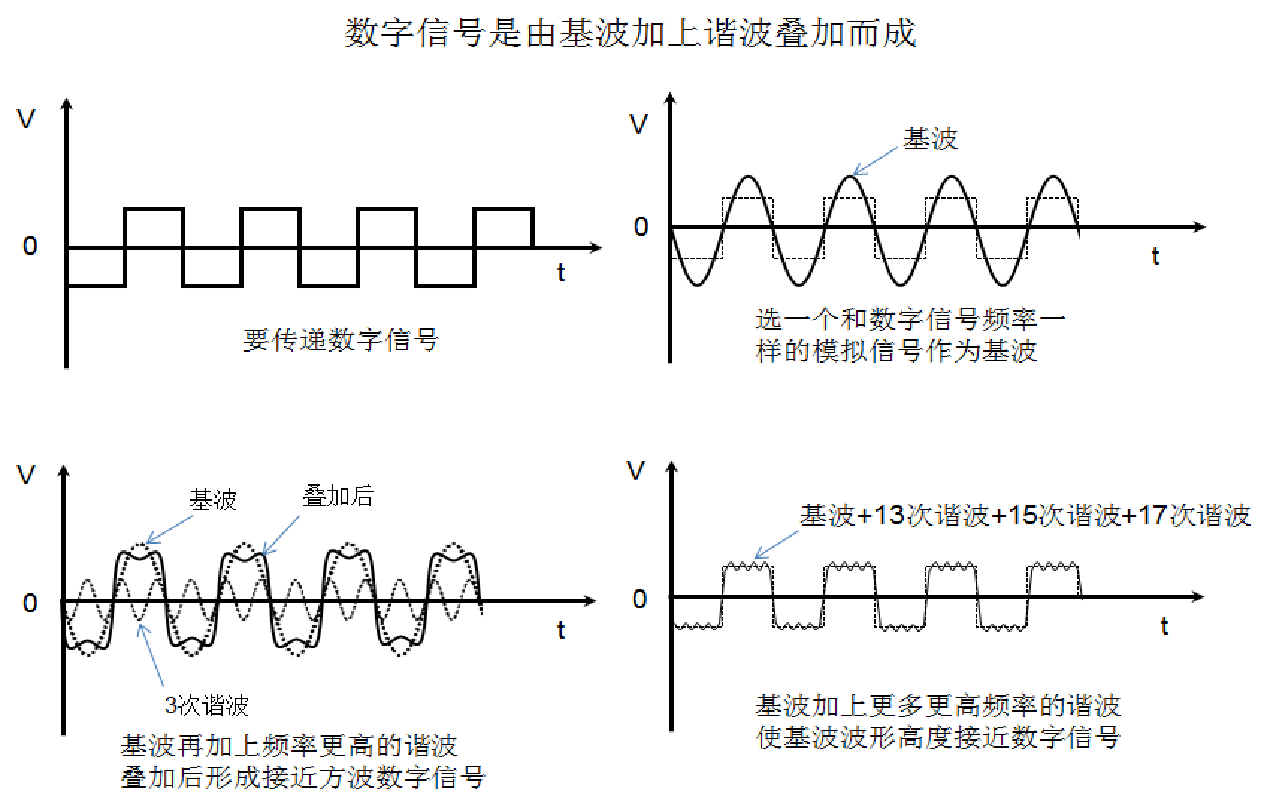
一个例题说明这个事情

也就是说,更高的带宽是为了容纳更多谐波,使得波形更接近方波,使得分辨更清晰

比特率和带宽的关系:正比

比特率是单位时间内发送的位数

为啥说单位时间内发送的位越多,要求的带宽就越大呢?

下图可以从直观上说明这个事情

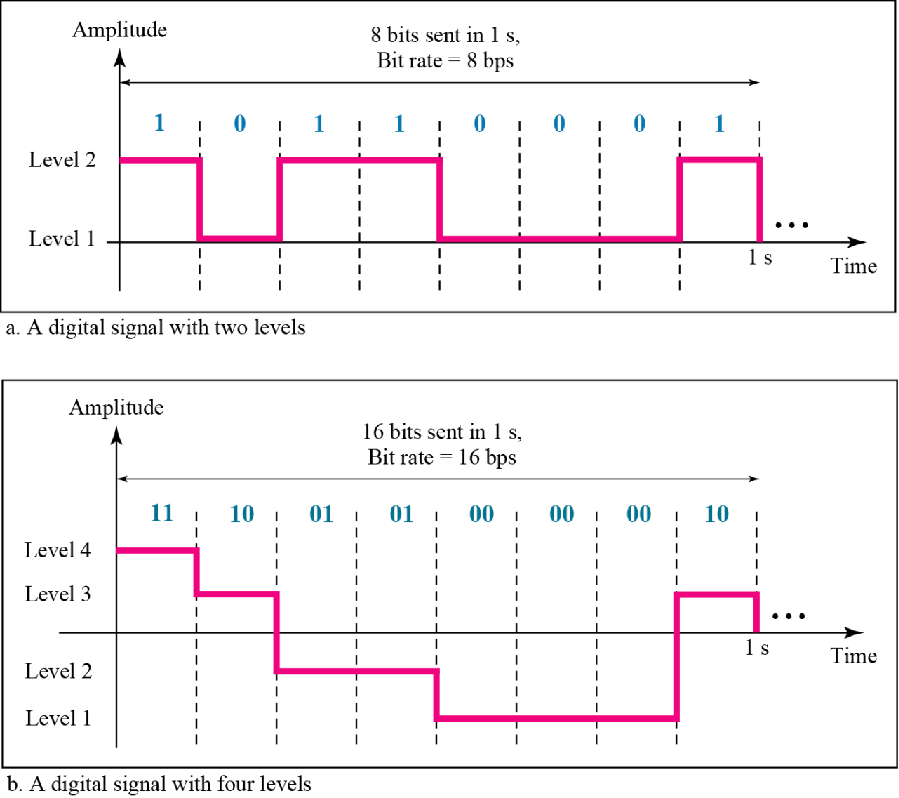
相同时间(1s)内,有四种电平的方波,可以发送16个比特位,比特率就是16bps

而只有两种电平的方波,只能发送8位,比特率就是8bps

也就是,要证明电平种类数越多,需要的带宽就越大

直观上,要拟合一个只有两种电平的数字信号,需要的谐波要少点.

也就是说这个方波越复杂,拟合时需要的谐波就要更多

但是怎么证明我不会

宽带传输

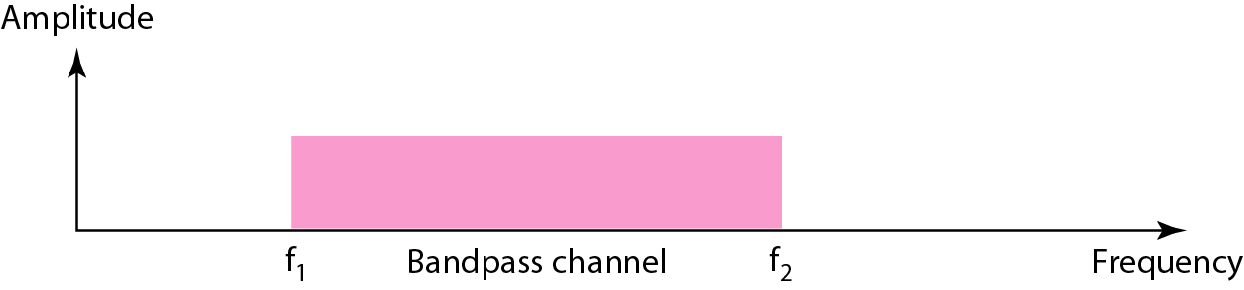
宽带传输允许的频率不是从0开始的,是从某一个正数f1开始的

"这就导致不能直接发送数字信号"为啥呢?

推测其原因是

1,是数字信号的主要分量(主要也就是振幅比较大,权重比较大的那些分量),其频率较低,在f1之下,会被噶掉,造成严重的失真

2,就算被噶掉的无关紧要,但是考虑衰减问题

可能发出时的信号很强,01分明,但是百前公里之后信号就会衰减,届时可能辱下图所示

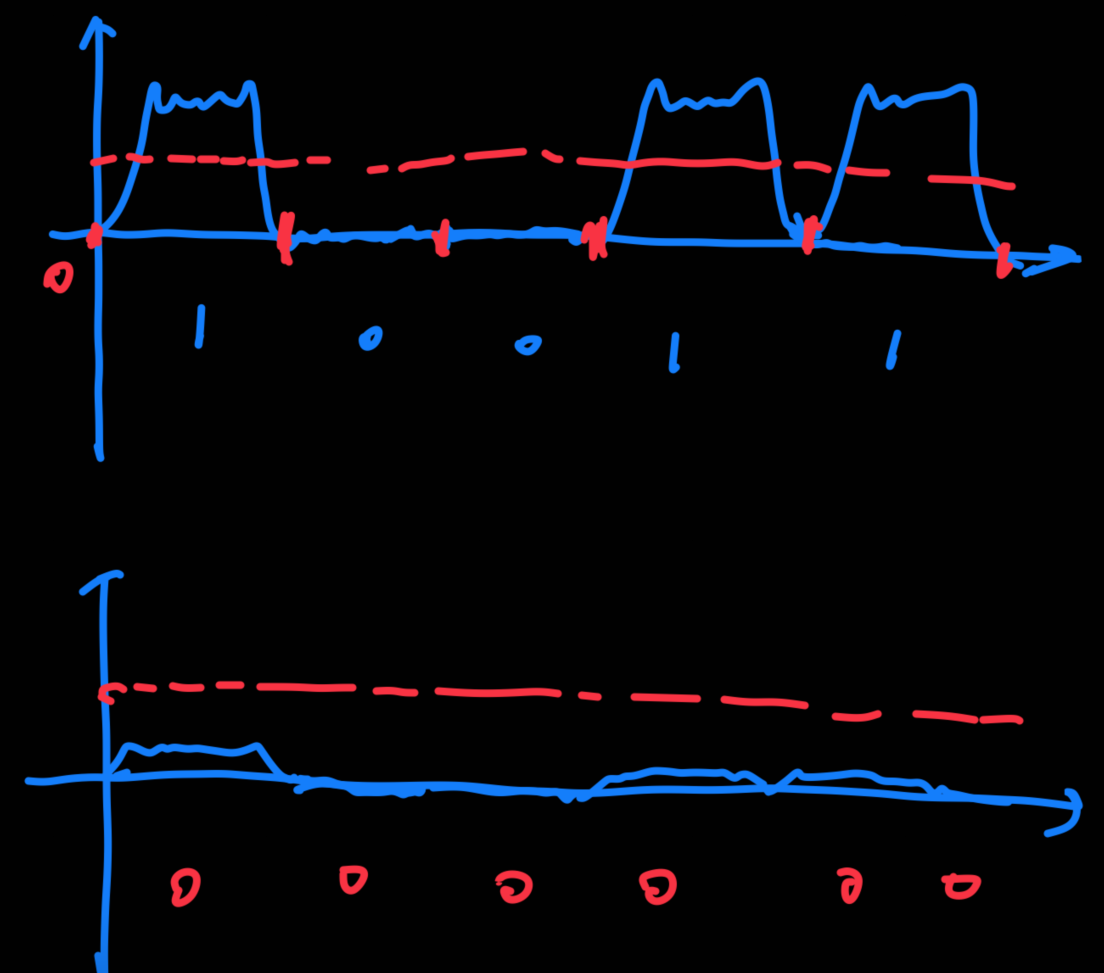
原来的高电位也变得低趴,被接收方识别为0

但是可以采取中继措施啊(~~比如红石中继器~~),上述推测2也不是问题啊

然而实际上也没有对数字信号采取中继,数字信号被应用于芯片比如CPU,计算机主板这种东西上,或者以太网这种局域网(曼切斯特编码等等)

那么为啥远距离传输一定要模拟信号呢

知乎的解答:

"以电话线为例子,电话线主要用来传语音（300到3400赫兹），不适合直接传输频带很宽能量比较集中在低频段的数字基带信号，所以这里需要一个modem做频带调制解调."

也就是推测1

那么为啥不能让电话线的最低频率再低一点,低到0?或者说,一根电线,其允许传播的电信号频率范围是多少?这个可以人为改变吗?

也就是说,计算机只会收发数字信号,两个modem之间才会使用模拟信号

flowchart LR
C1((C1))
C2((C2))
subgraph 远距离通信
	Modem1(Modem1)
	Modem2(Modem2)
end
C1--"数字信号"---Modem1
Modem1--"模拟信号"---Modem2
Modem2--"数字信号"---C2

在两个计算机看来,他俩是直接数字信号通信的,他俩不知道中间有个猫干了啥

flowchart LR
C1((C1))
C2((C2))
C1--数字信号----C2

传输减损

三种类型的减损:衰减,失真,噪声

衰减

衰减:远距离传输信息肯定有衰减,就比如在泰安说句话在西安听不见,可能十步之外就听不见了,这就是衰减

衰减的原因是介质震动将能量传递给其他物质了,比如空气

衰减只会让能量减弱,不会改变信号的频率相位,而能量直接提现到振幅上,因此画在图上,衰减就是信号变得低趴

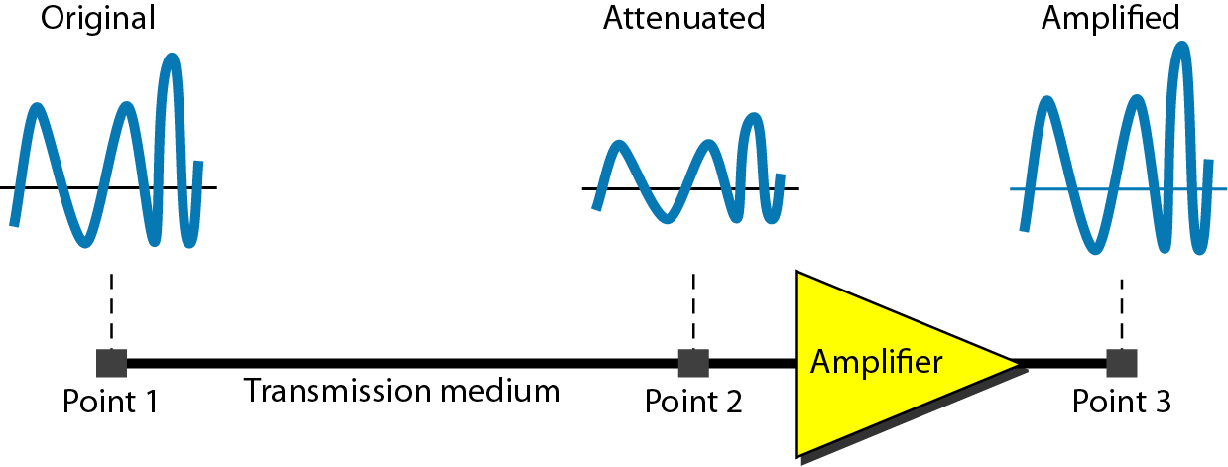
使用分贝作为单位衡量衰减程度 \[ dB=10\lg{\frac{P_2}{P_1}} \] 其中P1是衰减前的功率,P2是衰减之后的功率

假设功率衰减为之前的一半,$10\lg\frac{1}{2}\approx-3dB$

失真

失真就是信号波形发生了变化,相位,频率都可能变化

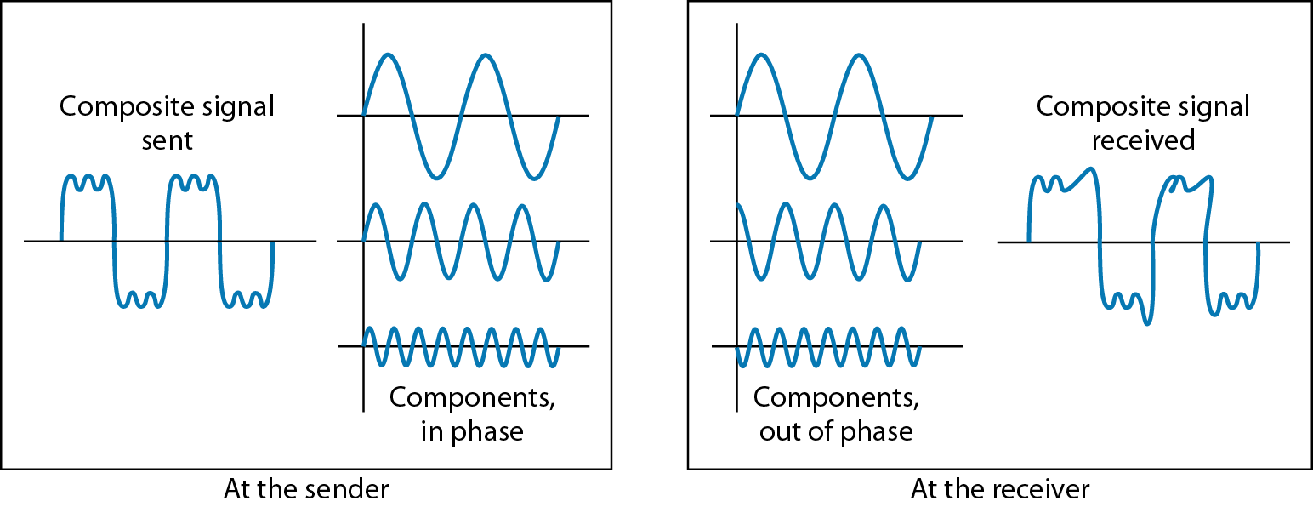
发生失真可能是电子元件本身导致,比如三极管就有失真区

噪声

噪声就是杂音,就比如上课时老师讲话是有效信息,学生嘀咕就是噪音

噪音能量大了,就会淹没有效信息,如下图所示

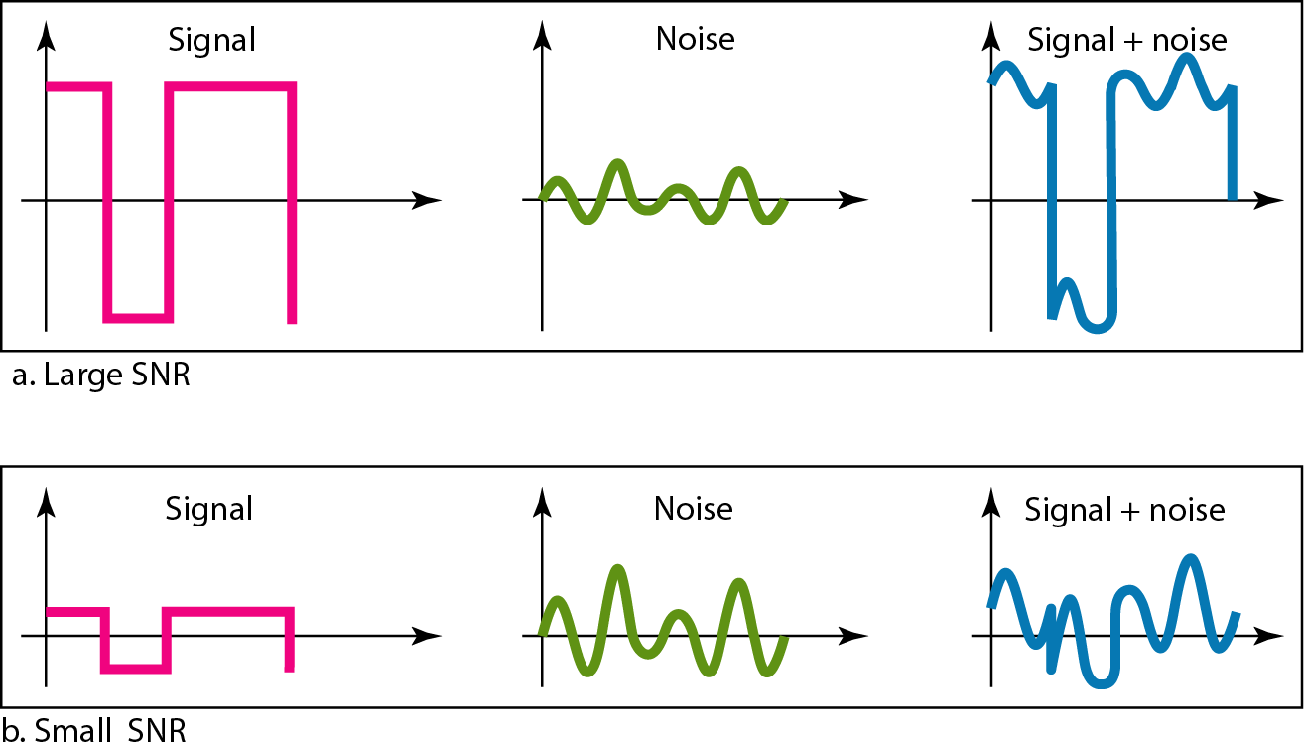
信号中的噪音可能来自

热噪音:导体中电子热震动造成

串扰:两条信号线之间的耦合、信号线之间的互感和互容引起线上的噪声。

脉冲噪声:磁暴就可以导致

噪声程度用信噪比衡量 \[ 信噪比SNR=\frac{平均信号功率P_{信号}}{平均噪声功率P_{噪声}} \] 单位是分贝

无噪声信道数据速率

数据速率(比特率):一秒内传送的比特数

三个影响因素:有效带宽,使用的信号电平数,通道质量

理论最大比特率(无噪声信道): \[ 理论上的最大比特率 = 2 × 带宽 × log_2 L， L是电平数 \] 如果只有两个电平,只能一个电平表示一位,

有四个电平,则每个电平可以编码两位

依此类推

但是,为啥带宽和比特率会发生关系呢?

参考深入理解奈奎斯特第一准则与码间串扰

奈奎斯特第一准则直观理解

考虑这么一个问题

同样一秒时间内,我让电平变化越快,岂不是传递的信息越多吗?

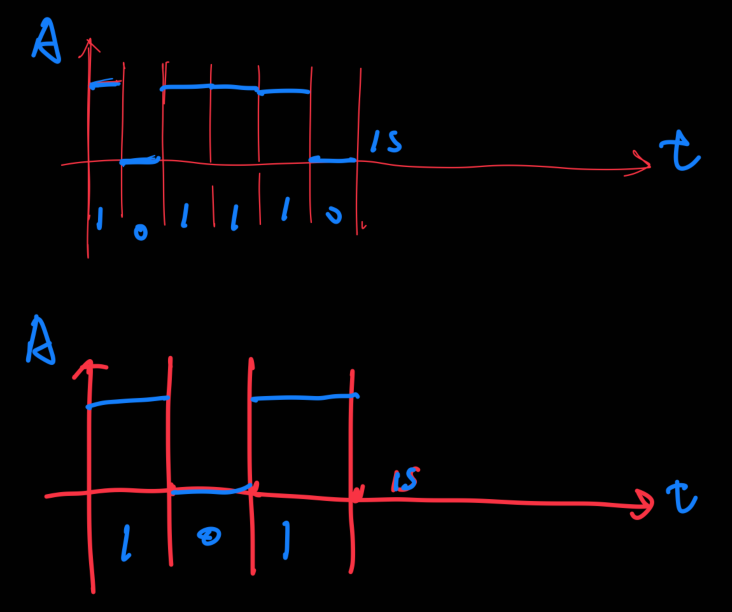
那么我让一个bit位持续时间只有1皮秒,那么1秒内直接传输1e9 个bit,岂不美哉?

这就是带宽的限制的作用了

单位时间内电位变化越快,说明信号的频率越大,显然信号的最大频率不能超过信道的频率上限.比这个上限再高的分量会被直接噶掉

最大比特率也就是说,在一秒内能够传递$ 2 × 带宽 × log_2 L$这么多bit,为啥不能比这再高了呢?为啥会和带宽挂钩,而不是和最高频率挂钩?

因为当比特率大于这个值时,会发生码间串扰

啥是码间串扰呢?

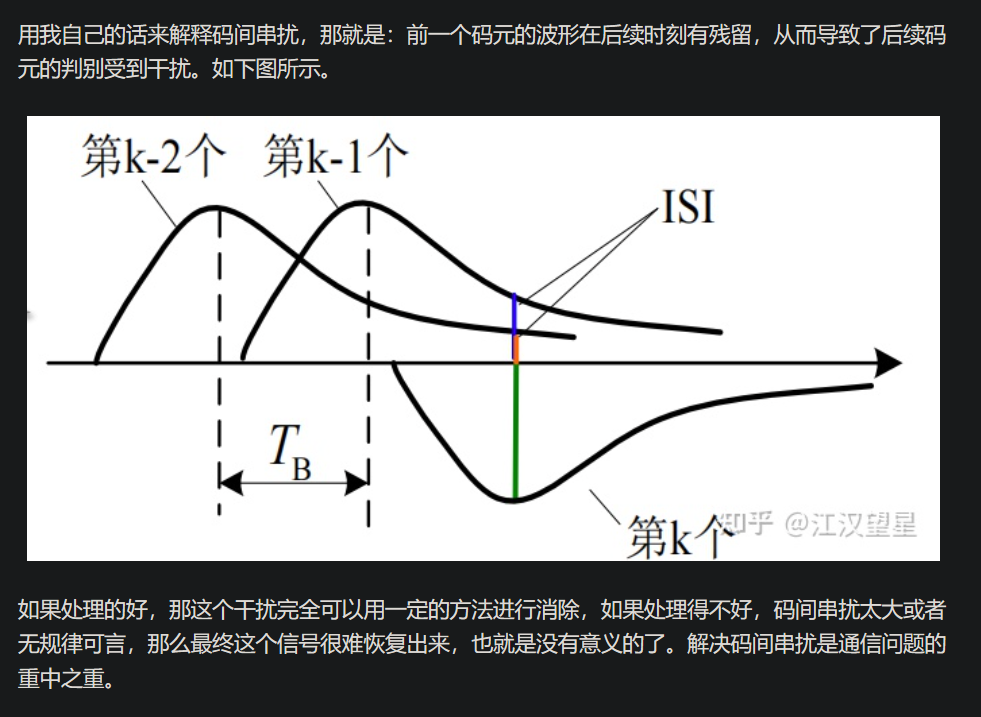
怎么发生的码间串扰?我有一个直观的理解了

发生器在产生一个码元之后,应立刻变换模式生成下一个模式,这里不应该存在码间串扰

为什么说前一个码元在后续时刻有残留呢?这个残留是怎么来的呢?

百度百科是这样解答的:

直方脉冲的波形在时域内比较尖锐，因而在频域内占用的带宽是无限的。

直观上,拟合一个尖锐变化的信号,需要无限多高频的分量

如果让这个脉冲经过一个低通滤波器，即让它的频率变窄，那么它在时域内就一定会变宽。

这是关键

首先,为啥信号频率变窄,时域就得展宽?

这是傅里叶变换的展缩特性展缩特性的推导

我没学过傅里叶变换的细节,找到一个直观的理解

因为脉冲信号是由不同频率的正弦波组合而成，通过低通滤波器，只剩下些低频正弦波，所以波形看起来更接近正弦波，像被展宽了一样。

也就是说,频率上噶掉高频和低频之后,再进行傅里叶逆变换,时域图像会变,变宽

此前是一个码元完毕立刻跟着下一个码元,现在每个码元都宽了,把脚伸到下一个码元怀里了,也就是"拖尾"

因为脉冲是一个序列，这样相邻的脉冲间就会相互干扰。这种现象被称为码间串扰（InterSymbol Interference，ISI）。

最后一个问题,为啥比特率超过这个最大值$ 2 × 带宽 × log_2 L$就会造成码间串扰?

实际上这个$log_2L$就是波特率,也就是码元率,也就是单位时间内传送的码元个数

这实际上是奈奎斯特第一准则

深入理解奈奎斯特第一准则与码间串扰

这篇博客完美解答了

写太好了写太好了写太好了

博主用一个实验证明了不遵守奈一准则的后果,实验是这样设计的:

首先,要发射方波,但是理想的方波的频率无限大,显然真实的信道做不到

于是用sinc脉冲函数作为近似拟合,该函数的带宽是2B,也就是说,该信号包括了2B带宽范围内的各种强度的连续频率的简谐信号分量,也就模拟了无噪声信道

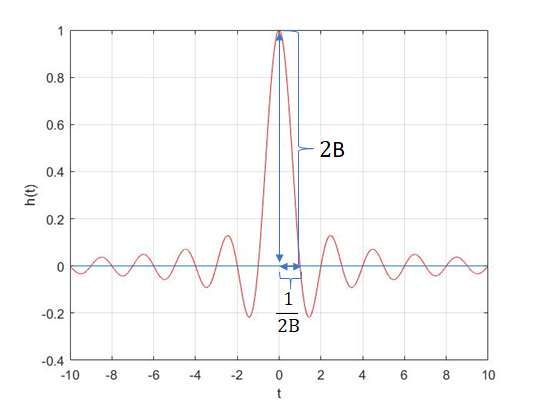
用这个最高的尖作为方波

要发送比特序列00010110,用正高电位表示0,负高电位表示0

对应电位处放上函数的尖儿

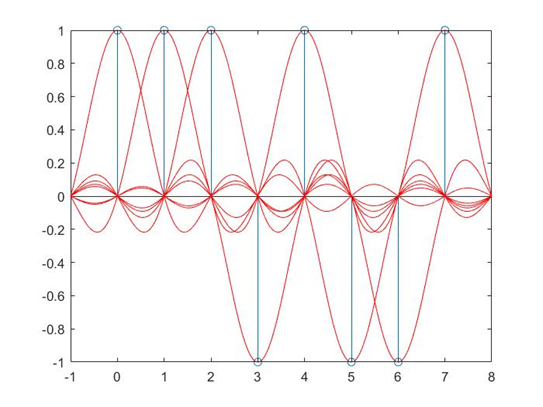
实际上发出的信号是这几个sinc函数的叠加

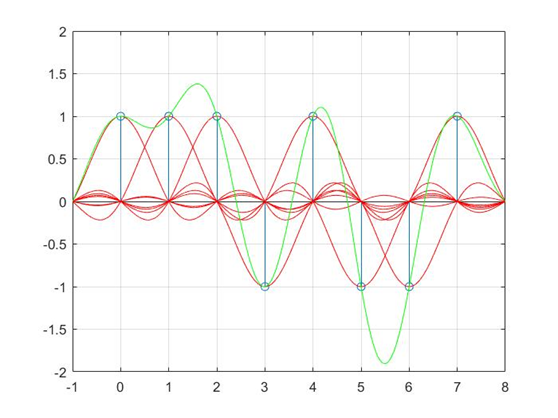
接收方收到后进行采样,决定某个时刻是哪一个码元

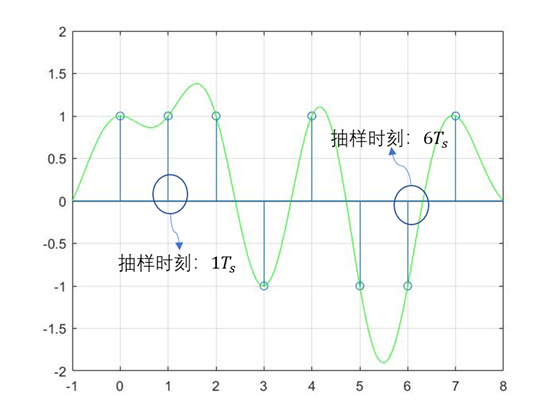
采样结果

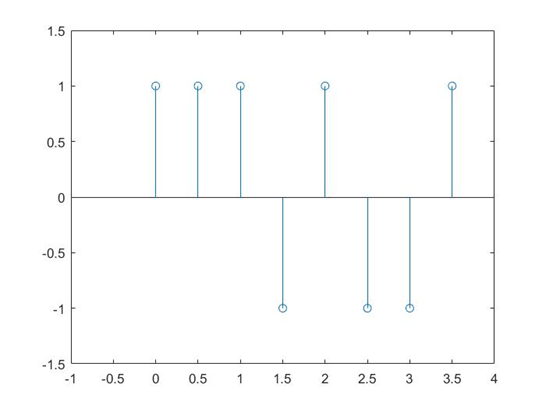
和发送时一模一样

好,下面要缩短码元的时间,也就是相同时间内企图发送更多的码元

之前是1秒内两个bit,现在是1秒内4个比特

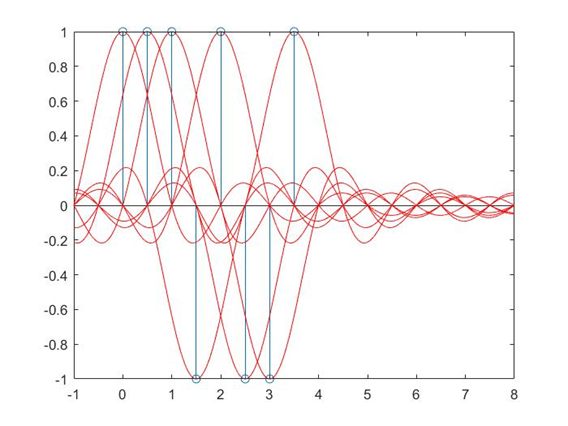
叠加之后

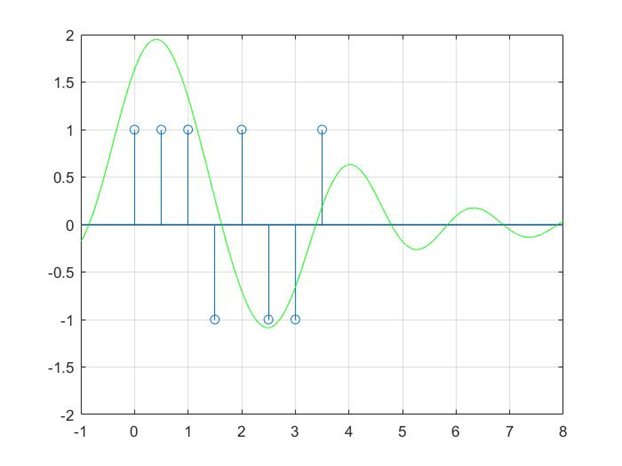
接收方采样

已经无法在整1和-1处采到信息了

如果以大于0的作为1,小于0的作为0

接收方得到的序列就是111101001,失真了

有噪声信道数据速率

定义通道容量:单位时间内通道传输的比特数

香农定理

\[ 通道容量C=带宽B\times \log_2(1+SNR)\\ \]

其中$SNR=\frac{P_{信号}}{P_{噪声}}$

如果SNR很大,可以认为$SNR\sim SNR+1$,则有 \[ C=B\times \log_2 SNR=B\times \frac{SNR_{dB}}{3} \] 香农定理规定了真实信道的最大传输速率

物理层 : 香农定理

然而香农定律中没有涉及电平数量,实际中也正好利用这一点,结合奈奎斯特准则计算信号电平数

有一个 1MHz带宽的通道。通道的信噪比是 63，合适的比特率以及信号电平是多少？

根据香农定律,理论上最高的通道容量为 \[ C=B\times \log_2(1+SNR)=1M\times \log_2(64)=6Mbits/s \] 实际上的比特速率肯定比这要小,为了获取更好的性能,可以使用$N=4Mbits/s$为合适的比特率

根据奈奎斯特第一准则 \[ N=2B\log_2L \] 得到$L=2$

这里的"性能"指什么呢?

性能

吞吐量

单位时间内成功传送的数据量.

单位:bit/s,bps,同带宽相同

吞吐量和带宽的区别:

带宽只需要考虑信道的速率,不管两头的计算机,发射装置

而吞吐量需要考虑所有因素,包括计算机的速度,调制速度,带宽等

可以理解为,带宽用来衡量一段高速公路满载时的流量

但是吞吐量需要考虑高速公路两头的收费站减速

因此吞吐量一定是小于等于带宽的

延迟

延迟 = 传播延迟 + 传输时间 + 排队时间 + 处理延迟

传输时间就是发送方计算机将信息从本机发到信道上的时间

取决于发送方CPU速度,总线,网络适配器等硬件的速度 \[ 传输时间=\frac{报文长度}{传输速度} \]

传播延迟就是信号从信道中传递的时间

传播延迟取决于信号在信道中的传播速度,比如电信号在导线中的速度就是光速$3\times 10^8$ \[ 传播延迟=\frac{距离}{传播速度} \]

排队时间就是该信号在接收方消息队列中等待被处理的时间

该时间取决于前面有多少个排队等待处理的消息以及这些消息的处理时间

处理延迟就是接收方执行本信号处理程序花费的时间

取决于接收方硬件速度,以及处理算法复杂度

带宽延迟积

定义了能够充满链路的位数

啥意思呢?

假如接收方在大洋彼岸,发送方传输一个bit,需要50ms才能抵达

而这50ms之内,发送方已经传输了成千上万个bit.

发送方一直传输,直到第一个bit到达接收方时,此时整个信道排满了bit

此时信道中的bit数量就是带宽延迟积

这一路上有多少辆车呢? \[ 带宽延迟积=延迟\times 比特率 \]

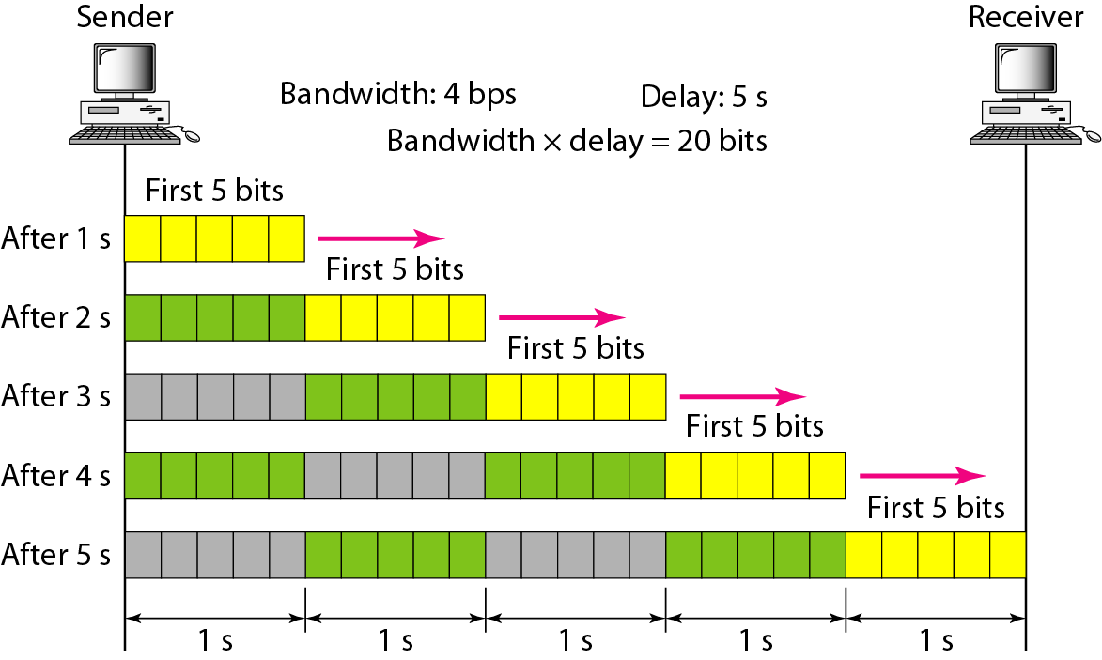
图中的带宽实际上描述的是数据速率,单位是bit/s

数字传输

线路编码

基本概念

将数字数据转换为数字信号的过程

数据元素:信息的最小单元,一个位bit

信号元素(码元):数字信号的最小单元,是数据元素的载体

比率r:每个信号元素承载的bit数量

把人比作数据元素,一个人相当于1bit

把车比作信号元素,一辆车是一个数据元素

比率为2,意思是一个信号元素承载两个bit,也就是一辆车可以坐俩人

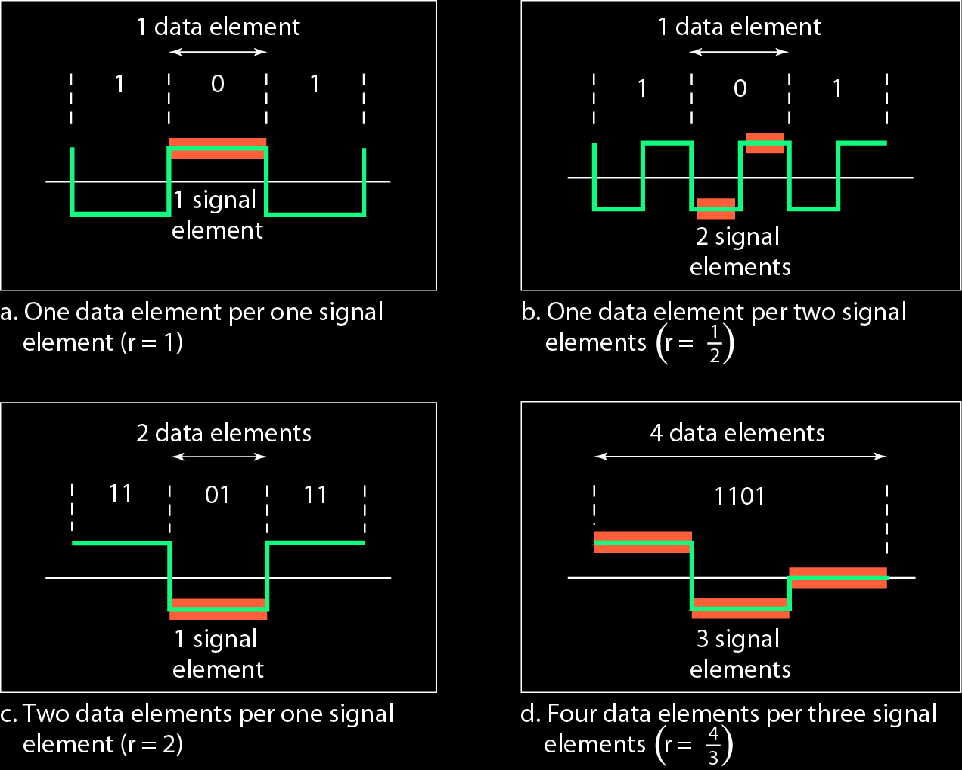
波形的每一个方格是一个信号元素,这个元素能够承载啥数据元素,承载几个,这是人为规定的

数据速率(比特率):一秒内发送的bit数

信号速率(波特率):一秒内发送的码元个数

两者关系: \[ S=c\times N\times \frac{1}{r},\\ \]

S,信号速率
N,数据速率
c,情形因子,通常取值1/2
r,比率

理想的数字信号,其带宽应该是无限大的,但是实际上信道的带宽有限,于是就有了奈奎斯特第一准则,对带宽的限制 \[ 理论上的最比特率 = 2 × 带宽× log_2 L， L是电平数 \] 也就是 \[ B_{min}=\frac{N_{max}}{2\times \log_2L}=\frac{cN}{r}=S \]

这里数据元素和信号元素的关系体现在电平数量上$r=\log_2 L$

线路编码需要解决的问题

基线偏移

接收方需要观察信号一段时间,才能计算出信号的平均功率,然后根据信号的瞬时功率决定当前信号是高电位还是低电位

假如使用高电位编码1,低电位编码0

然后发送方故意找茬发了一亿个1,接收方认为平均功率就是10V电压对应的功率.如果后来的1,其电位稍微低了点,成了8V,接收方就会把它解码为0

尽量避免基线偏移就得选择正负电位出现几率相同的编码方式

直流分量

一个信号可能会有变化很剧烈的地方,也可能会有变化比较缓慢的地方

比如如果发送方连续发送一亿个1,那么信号就可能是持续1秒的高电位,几乎成为了直流电

直流电无法通过电容这种器件.会被过滤掉

尽量避免直流分量,就得选择变化剧烈的编码方式

自同步

就是"对表",接收方得和发送方时钟差不多一致

否则可能出现下图情况

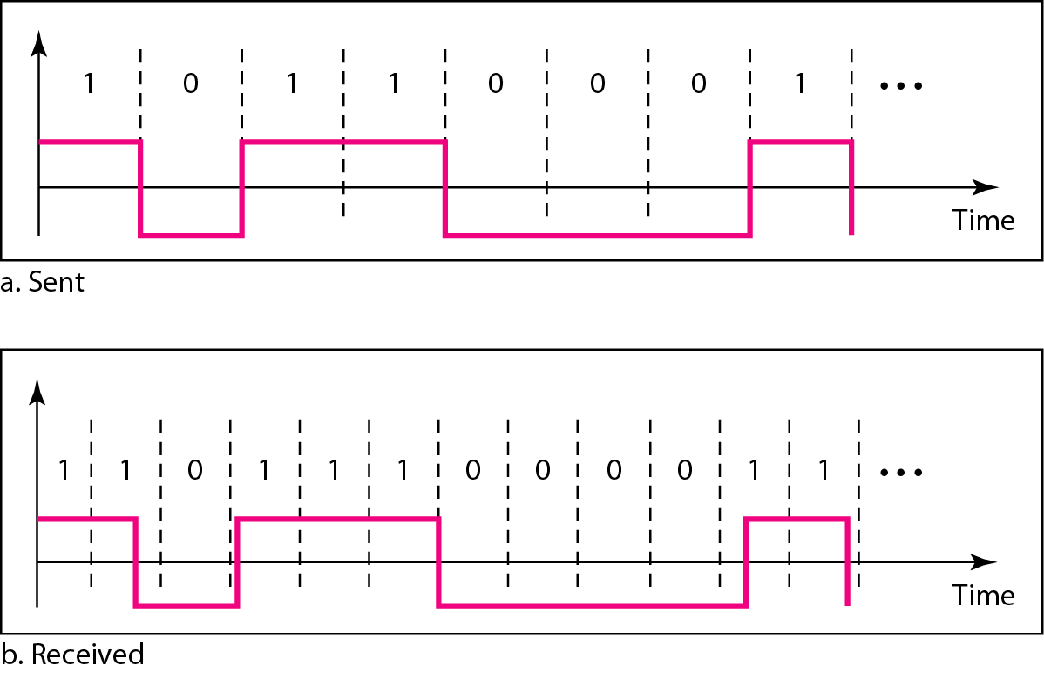
差错检测

抗噪声,抗干扰

实现的复杂性

线性编码方案

性质	编码方案	图像	特点	带宽和数据速率
单极性	不归零(NRZ)		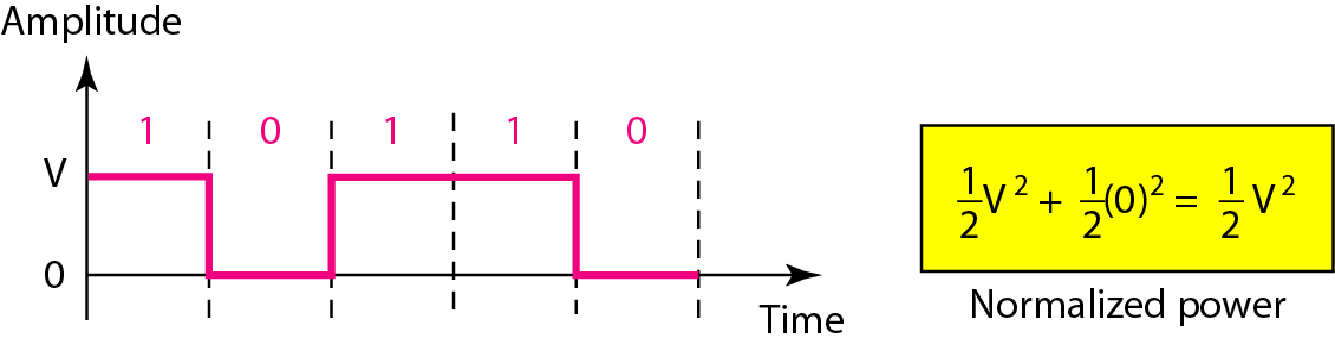1高0低	$B=\frac{N}{2}$
极性	不归零(NRZ)		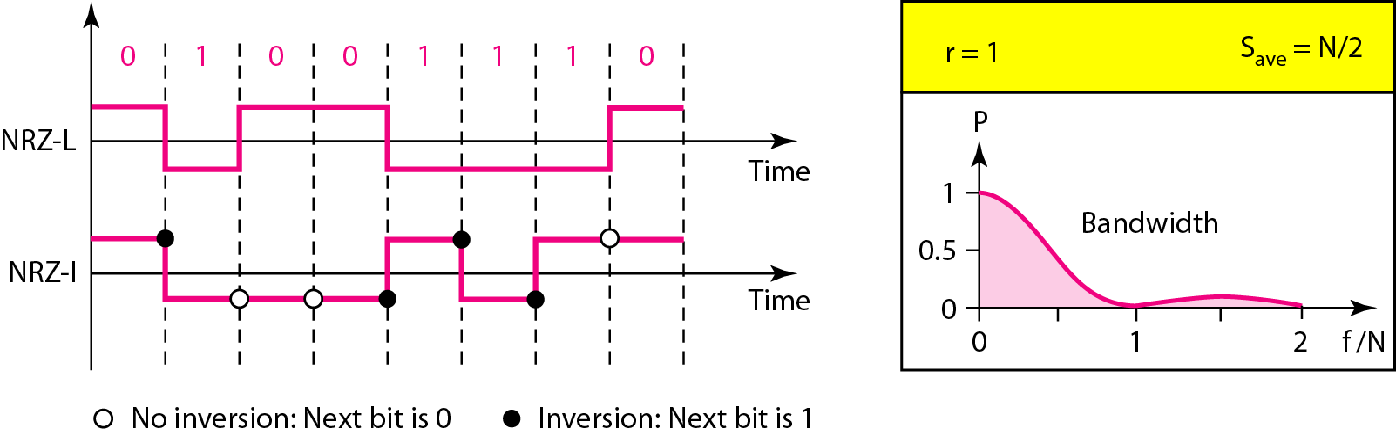NRZ-L:0正1负 NRZ-I:遇1则拐	$B=\frac{N}{2}$
极性	归零码(Polar RZ)		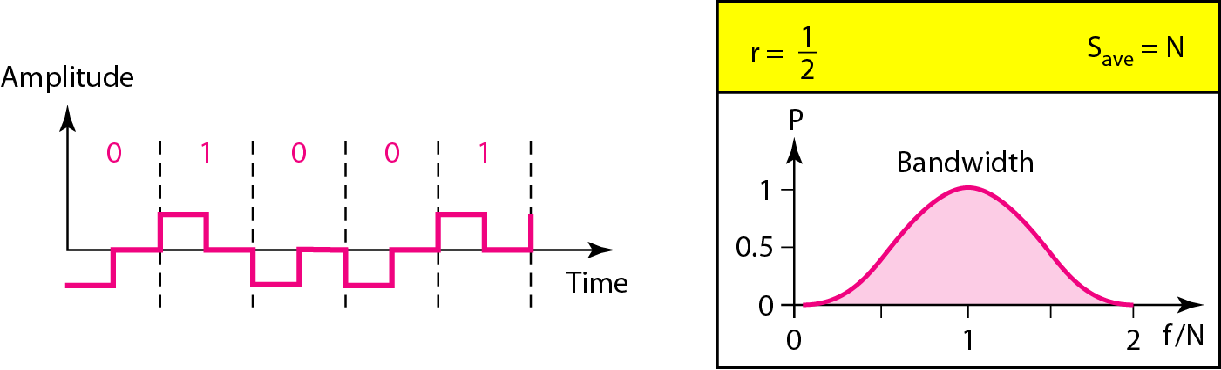0先负后0 1先正后0	$B=\frac{N}{2}$
极性	双向码曼彻斯特编码差分曼彻斯特编码		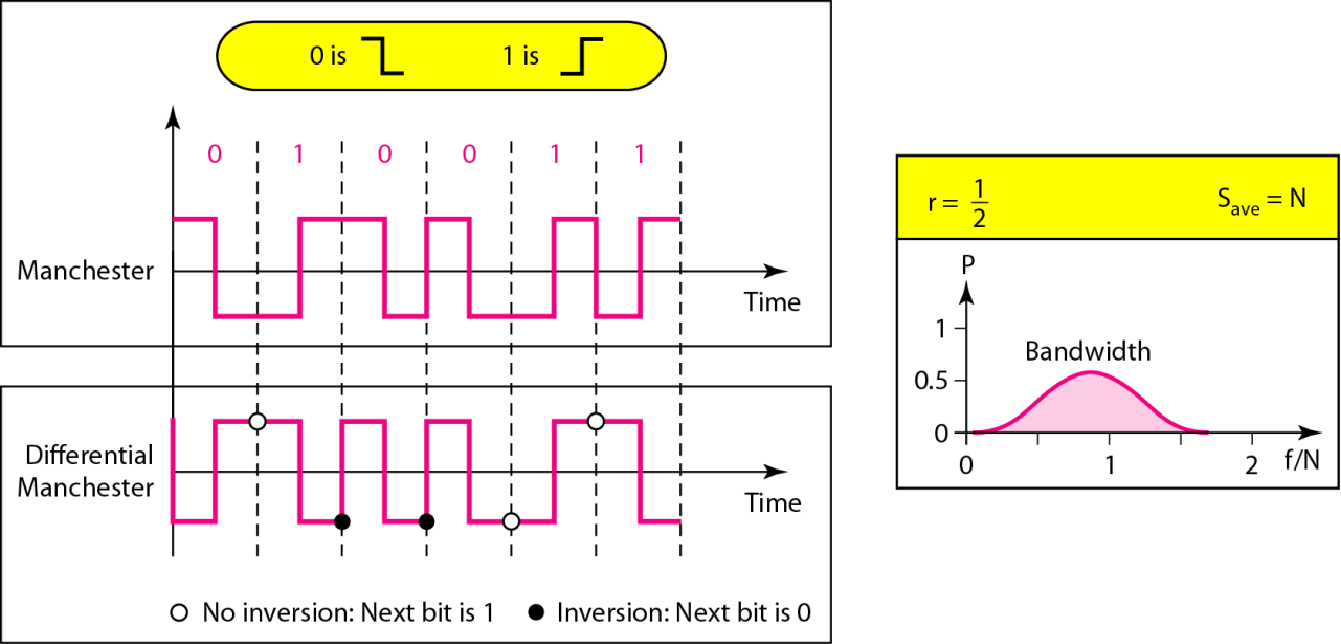曼彻斯特:0先负后正,1先正后负差分曼彻斯特:1先保持,0立刻转	$B=\frac{N}{2}$
双极性	交替传号反码(AMI) 伪三元编码(Pseudoternary)		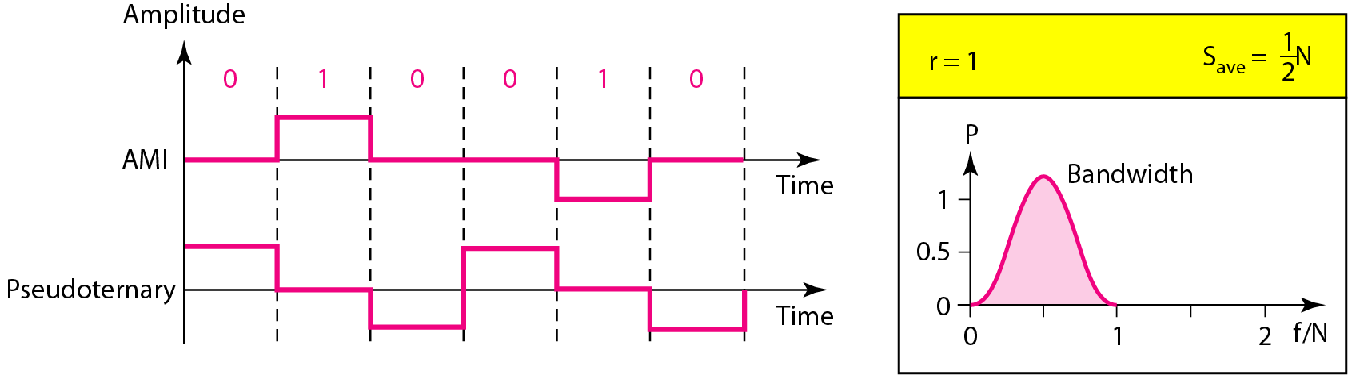AMI:1正负交替,0就是0 Pseudotemary:0正负交替,1为0	$B=N$
多电平mBnL m个数据元素编码成n个信号元素也就是n个码元承载m个bit	2B1Q(L=4=Q)	2B1Q: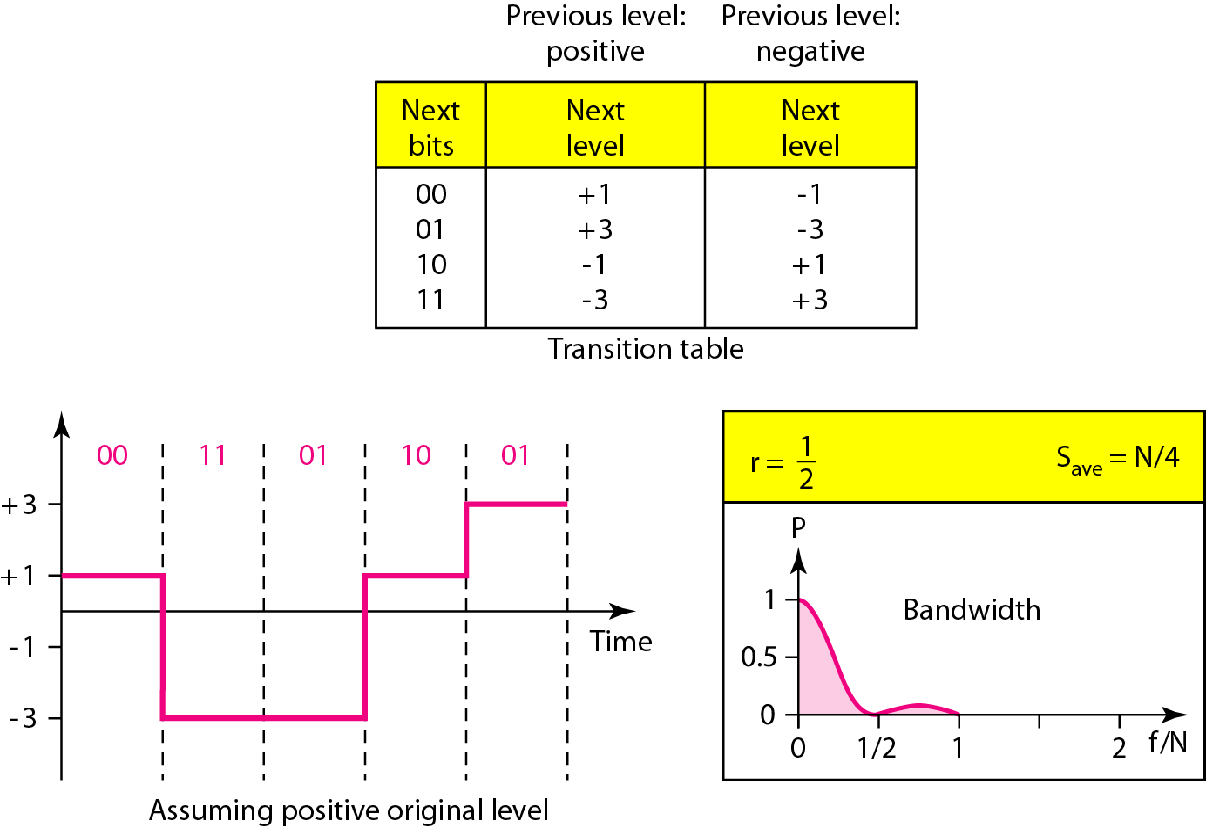 8B6T:	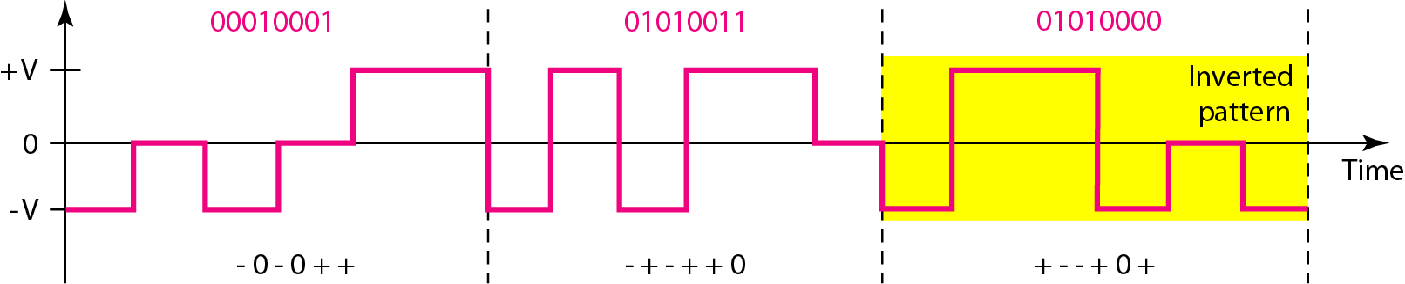多个电位,可以用连续的几个电位编码连续的几个bit 比如2B1Q意思是,每两个bit为一个组,有4种电位,一组使用一个信号单元(码元),也就是$r=2$ 比如8B6T意思是,每8个bit为一组,有3种电位,一个组使用连续的6个信号单元(码元),也就是$r=8/6=4/3$	2B1Q:$B=\frac{N}{2}$ 8B6T:$B=\frac{3N}{4}$
多电平并发	4D-PAM5 四线路并发的8B1Q		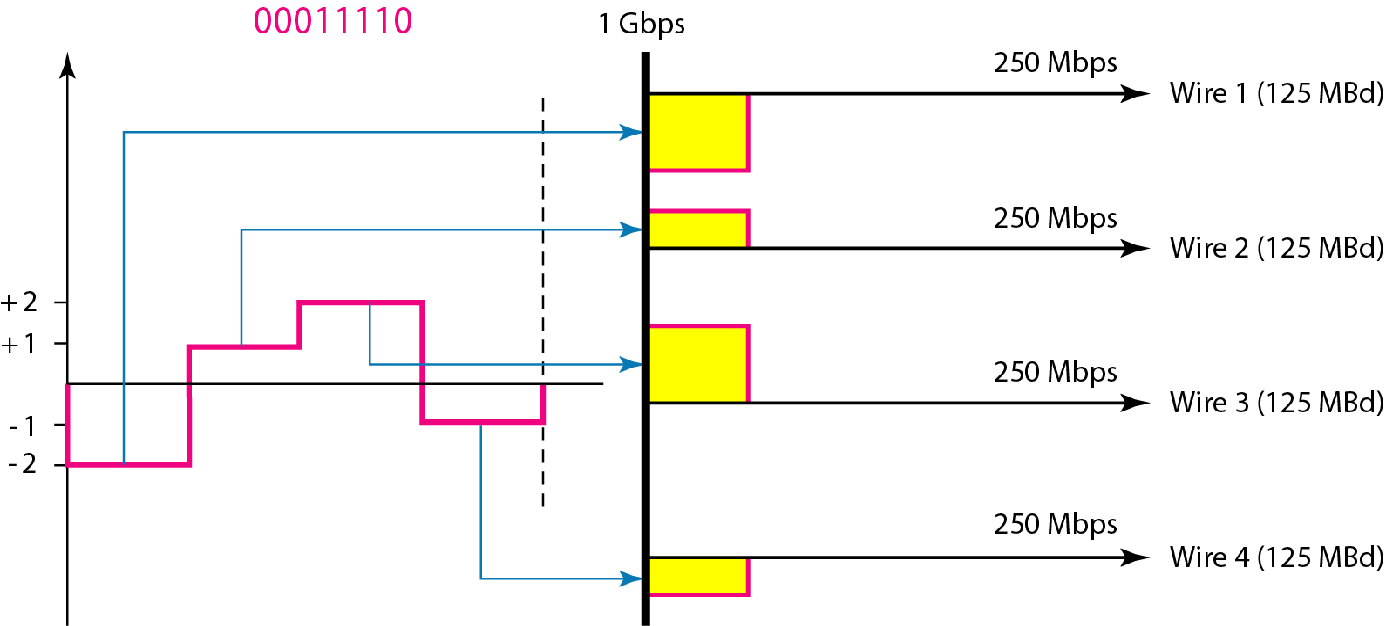00对应-2电位 01对应1电位 11对应2电位 10对应-1电位从四根铜线上并发传送如果只有一根线,则相当于8B1Q	$B=\frac{N}{8}$
多线路	MLT-3 三电平多线路传输		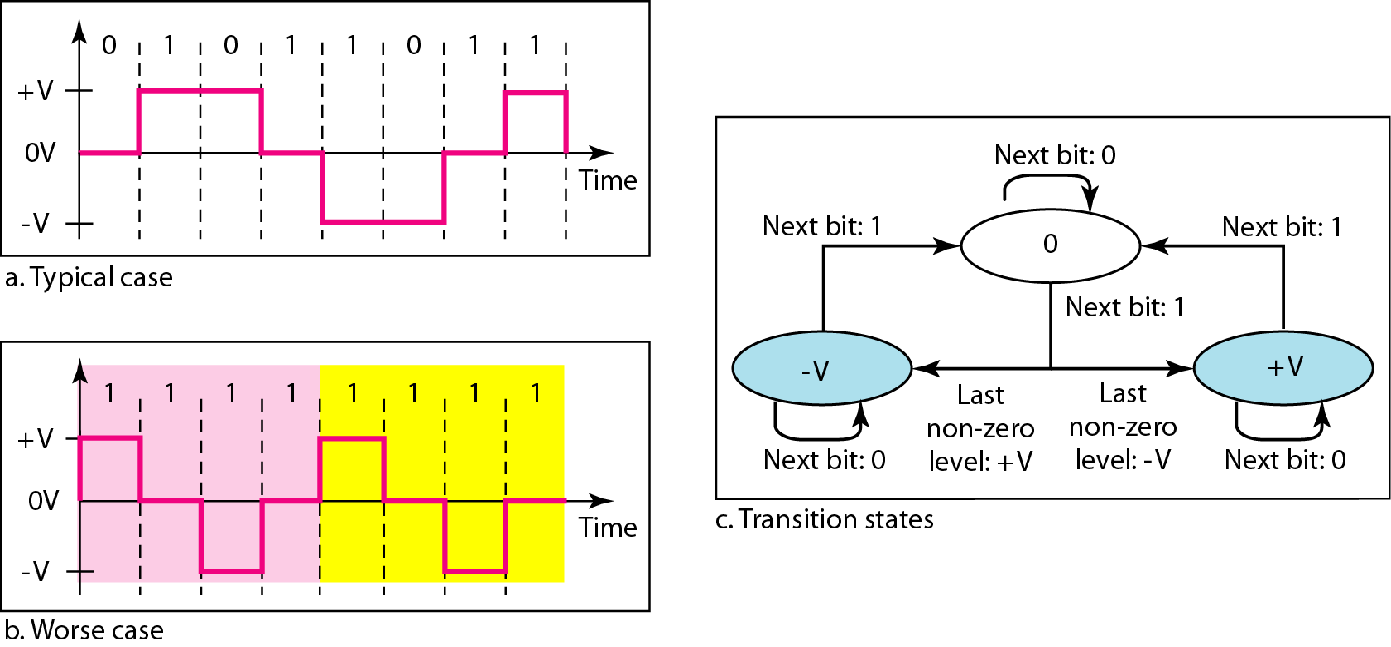跳变方式多于两种,之前的极性非极性编码都只有两种跳变方式.而MLT-3中的跳变多余两种跳变规则: 如果下一位是0，没有跳变如果下一位是1且当前电平是0，下一个电平是最后一个非零电平的相反值如果下一位是1且当前电平不是0，下一个电平是0	$B=\frac{N}{3}$

块编码

块编码,mB/nB编码,将m个bit加上额外的位组成nbit(n>m)

其目的是加上冗余信息,确保同步,并获得差错控制能力

或者说有一定的加密能力

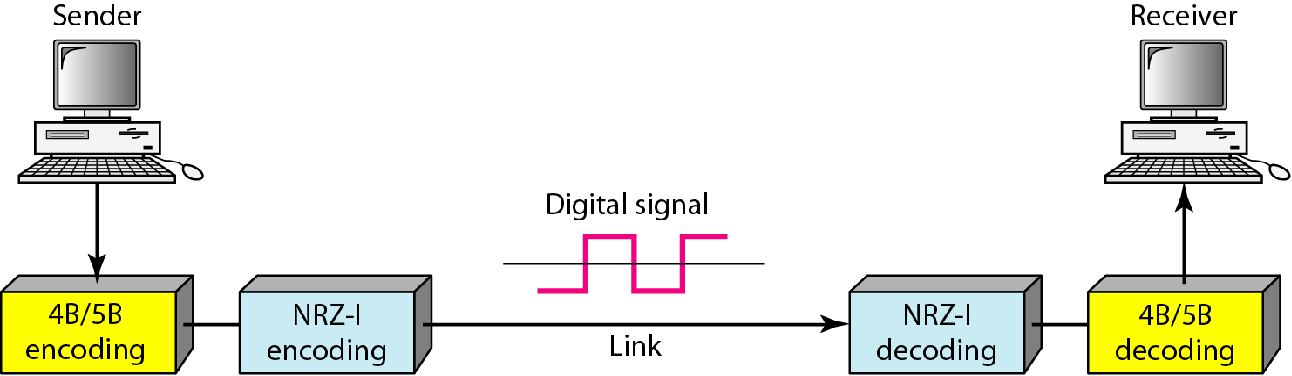
计算机发出的和接收到的仍然是裸数据,mB/nB编码和解码器屏蔽了这个添加/去掉冗余的过程

具体如何编码呢?以4B/5B为例

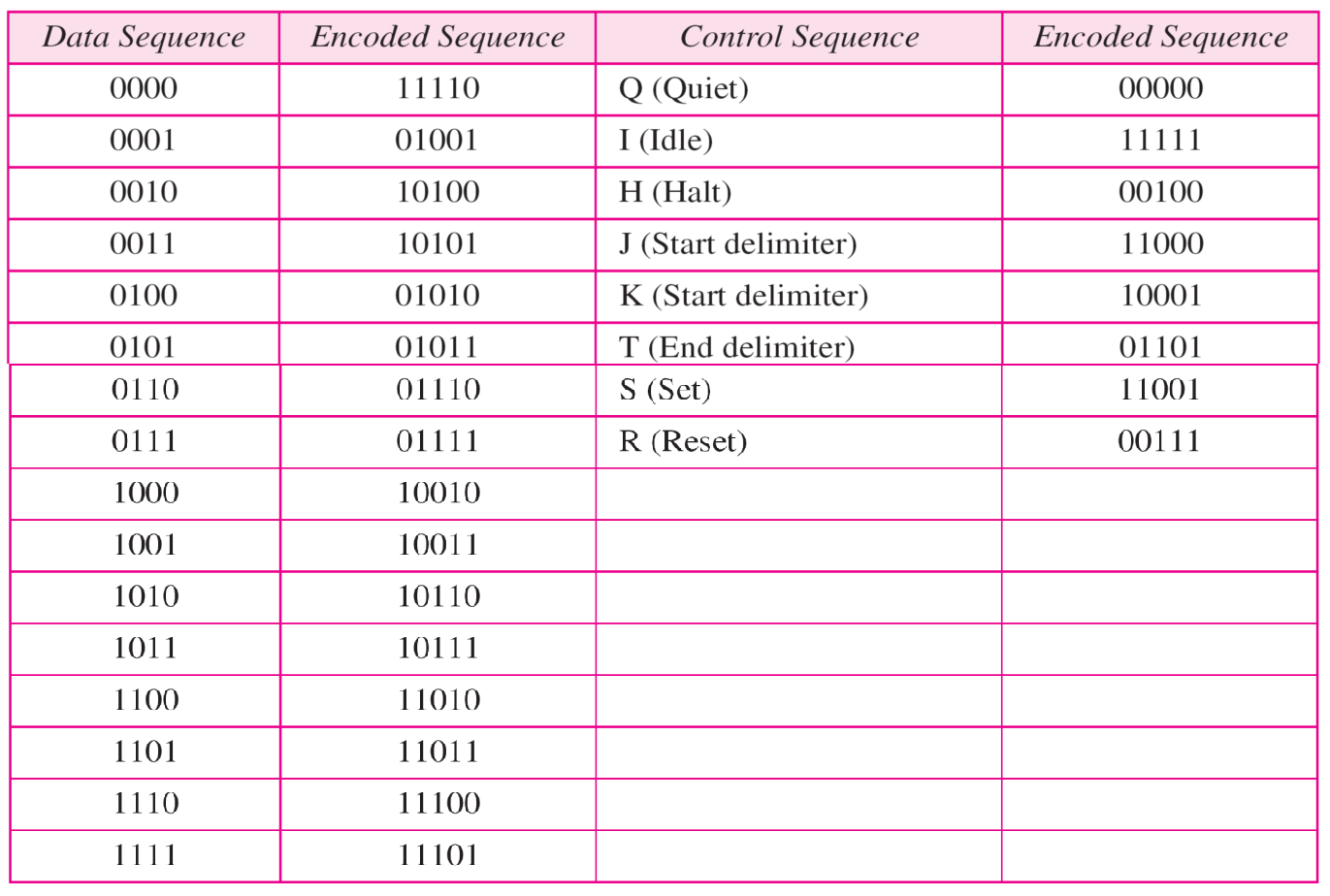
冗余组:使用了5位,实际上只有4位满编,也就是说,有$2^4$个编码是有实际意义的

剩下的$2^5-2^4=16$个编码就是冗余组,可以另外定义意义

扰码

扰码用于解决什么问题?

先说之前的编码方式的缺点

双相码适用于LAN中间站的专用链路，不适用于长距离通信；

块编码和NRZ编码的组合有DC分量，也不适合于长距离通信；

双极性AMI带宽窄且没有DC分量，但连续0的长序列会失去同步。B8ZS和HDB3

扰码就是为了解决这些问题

咋解决呢?避免出现连续多个相同的电位

扰码编码方式	图像	特点
B8ZS		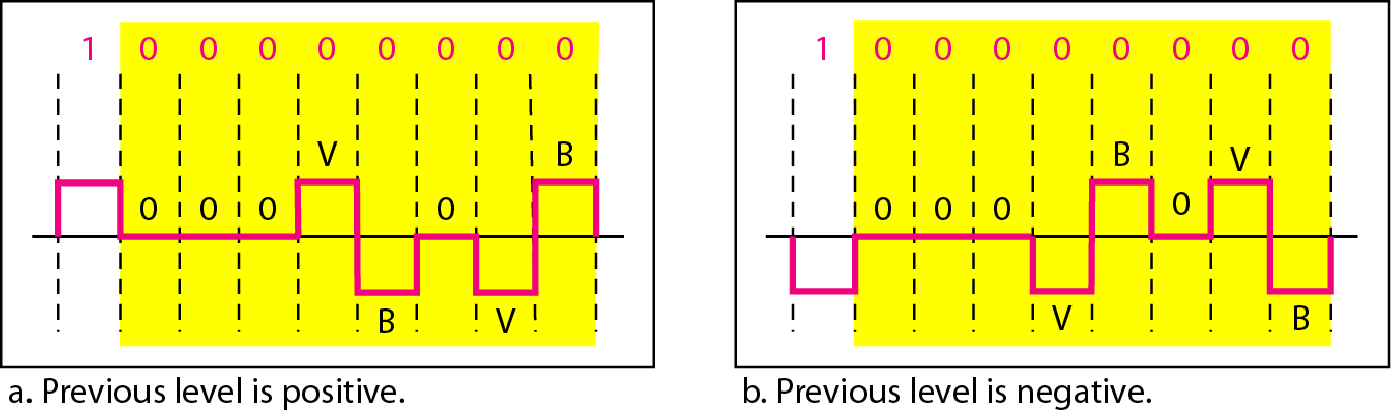连续的八个0会被替换为000VB0VB
HDB3		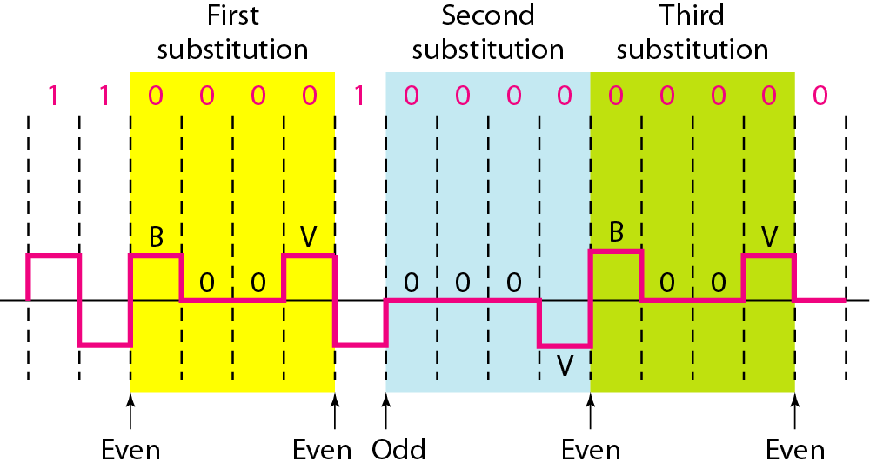4个连续0电平被置换成000V或B00V；两个不同的置换是由于为了维持每次置换后非零脉冲为偶数；如果最后一次置换后的非零脉冲数是奇数，置换为000V，使得非零脉冲总数为偶数；如果最后一次置换后的非零脉冲数是偶数，置换为B00V，使得非零脉冲总数为偶数。

模拟信号调成数字信号

两种方式:PCM或者Delta

PCM

模拟信号调制成数字信号

没看错,就是模拟信号调制成数字信号,不是解调

这就奇怪了,远距离传送信号的时候都是在发送端先把数字信号调制成模拟信号,然后接收端模拟信号再解调成数字信号.但是PCM里是故意把模拟信号调制成数字信号的

实际应用?比如要研究星球脉冲的规律.由于这个星球每时每刻都在发射信号,在时域上是连续无限的.计算机首先需要存储了数据然后才能分析.

怎么存储就是问题了,如果保留半小时内的观测数据,也是有无穷多的时间点的.

可以选择每1分钟记录一次,或者每一秒,每一毫秒记录一次.

这样就把一个连续的模拟信号采样成离散的数字信号了

这个过程如图所示

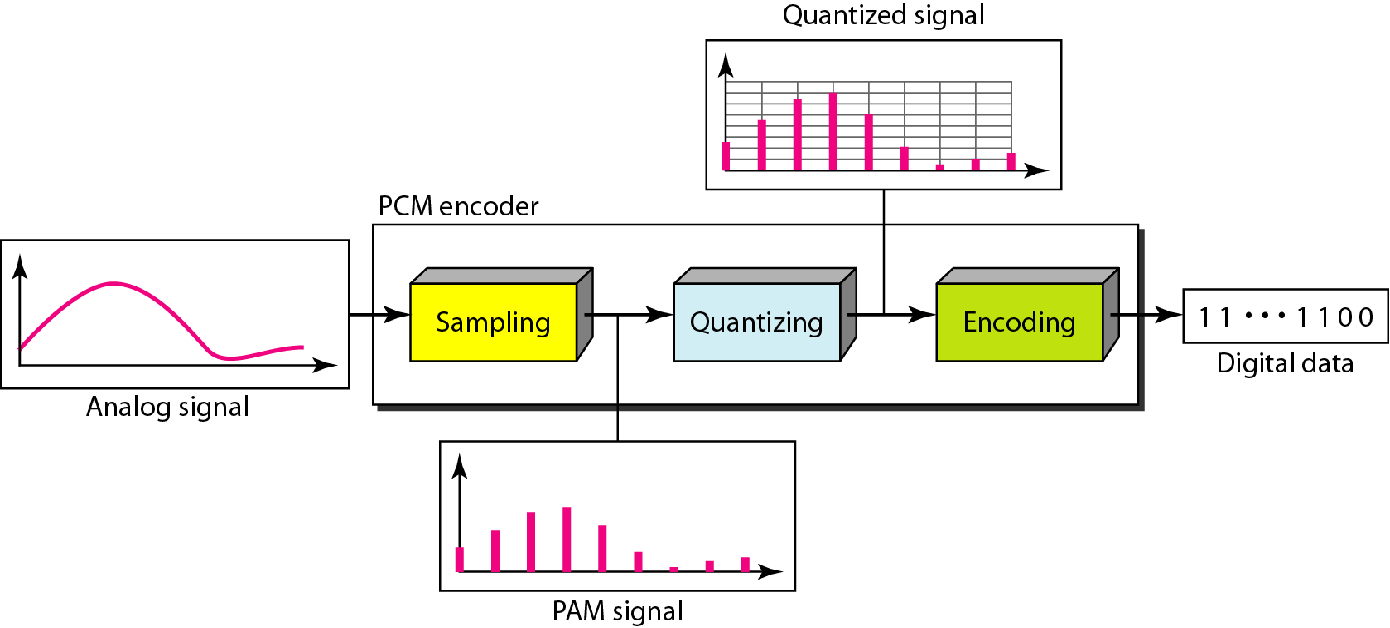
采样

采样率:单位时间内采取的离散信号的个数,单位,Hz

根据奈奎斯特定律,采样率必须是信号最高频率的两倍

为啥呢?下图意思意思

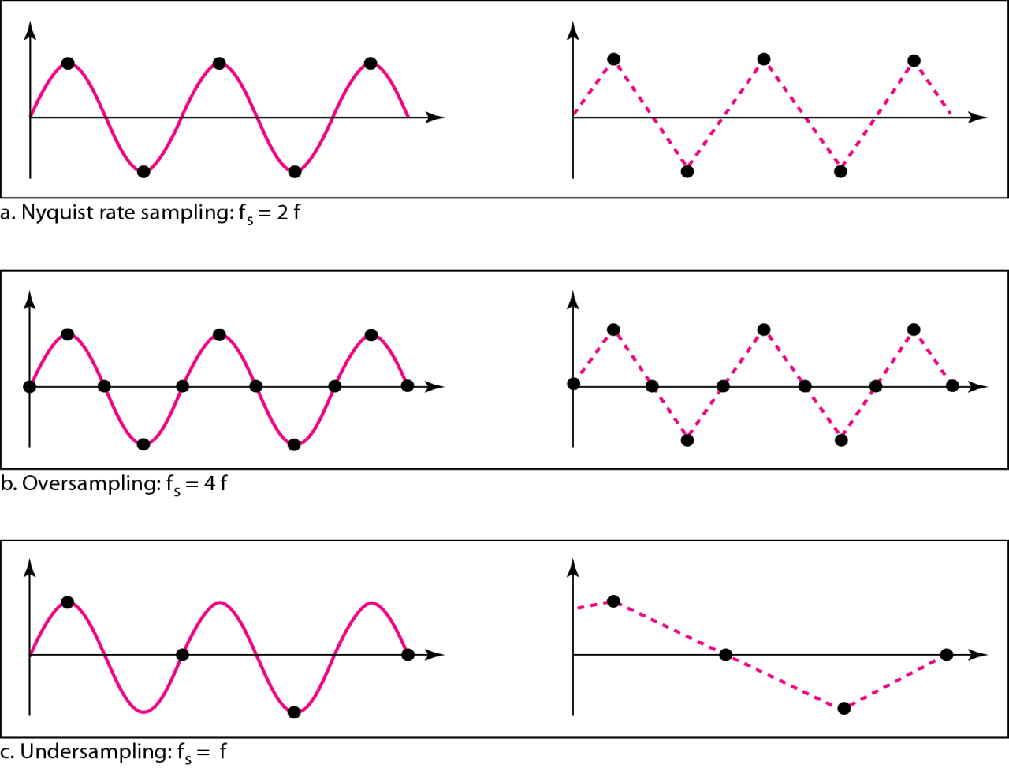
量化

采样之后,离散的信号振幅也是一个不规整的值,现在规定几个固定的"合法振幅",让这些离散信号振幅舍入到最近的"合法振幅"

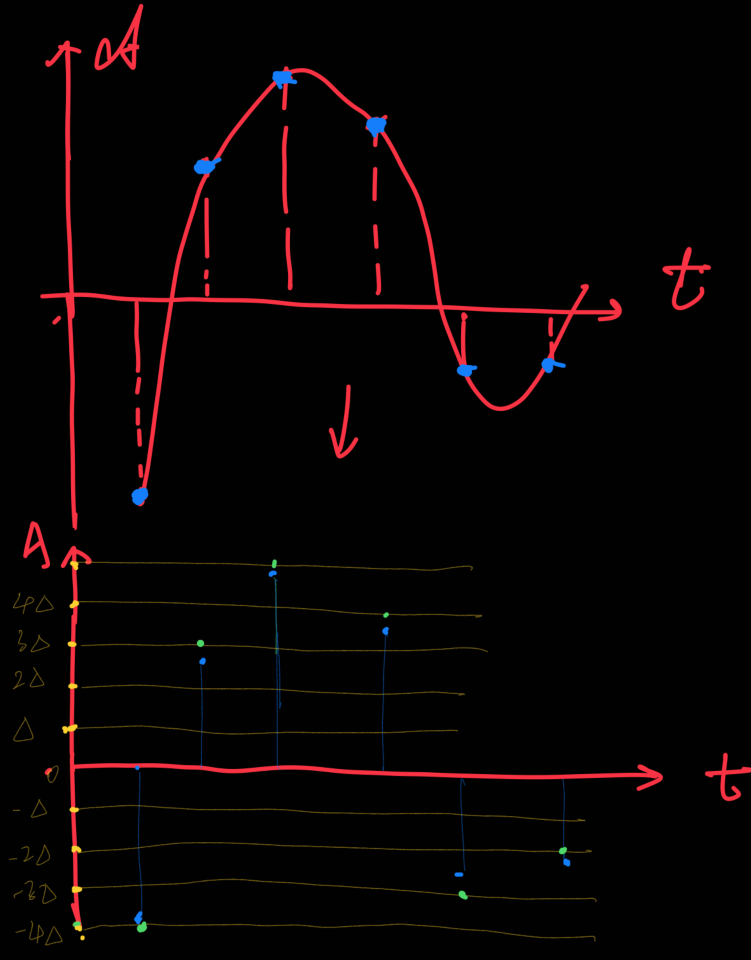
怎么选取"合法振幅"呢?

假设要分成L=10个区间($-5\Delta,-4\Delta,-3\Delta,....,0,\Delta,2\Delta,5\Delta$),

设离散信号振幅值的最大和最小值分别为$V_{max},V_{min}$

那么一个delta的高度就是 \[ \Delta =\frac{V_{max}-V_{min}}{L} \] 然后原来的各点就近似为各自最近的"合法振幅"

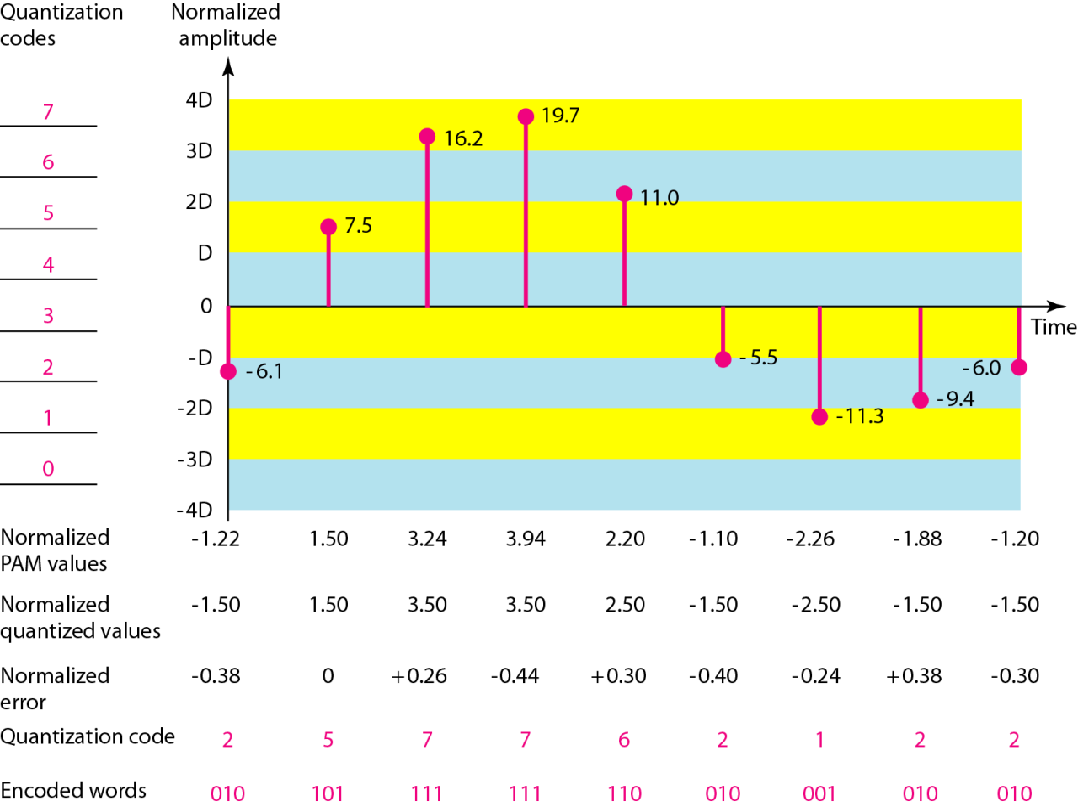
量化误差

L越大,每个Delta越小,分的阶层越多,近似就越少,误差就越小 \[ SNR_{dB}=6.02n_b+1.76dB \]

这里$n_b$是每个样本需要多少位表示

在[-4D,4D]中有8个"合法振幅"等级,那么要编码一个合法振幅就得用$\log_28=3$个bit

因此在这里$n_b=3$

分层越多,也就是$n_b$越大,信噪比越大,也就是噪声的影响越小,也就是越准确.

编码

量化等级L,也就是分层个数越多,表示一个采样数据所需要的bit位数就越多 \[ n_b=\log_2 L \]

因此可以得到

\[ 比特率N=采样速率f_s \times 每个样本的位数n_b \]

人语音的频率范围是$[0,4k]Hz$,假设要数字化人的语音,每个样本有8位,比特率是多少?

根据奈奎斯特定律,采样速率得是最高频率的两倍,也就是说$f_s=4kHz\times2=8kHz$

那么比特率就是: \[ N=f_s\times n_b=8k\times 8=64kbps \] 电子包浆音乐应该就是量化等级太低导致的

带宽

\[ B_{min}=cN\frac{1}{r} \]

c,情形因子,取1/2

r,码元和携带比特位的比例,在NRZ或者双极性编码信号中r=1

N,传输速率,比特率$N=f_s\times n_b$

$f_s=2f_{max}$采样率,信号最大频率的二倍

$n_b=\log_2 L$,每个样本的位数

带入得到 \[ B_{min}=\frac{1}{2}\times 2f_{max}\times n_b=f_{max}\times n_b \]

传输方式

并行

串行,包括同步,异步,等时

并行

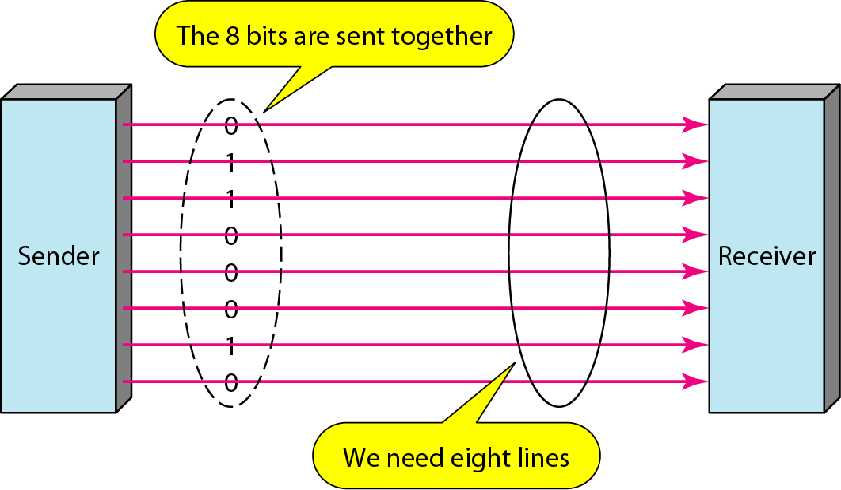
同时传送nbit,就需要n根线

串行

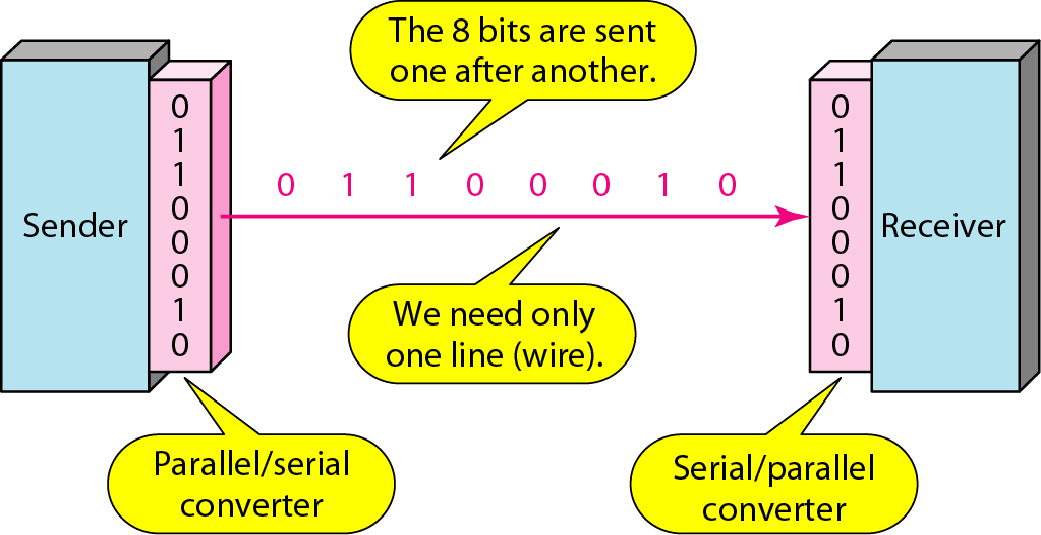
异步传输

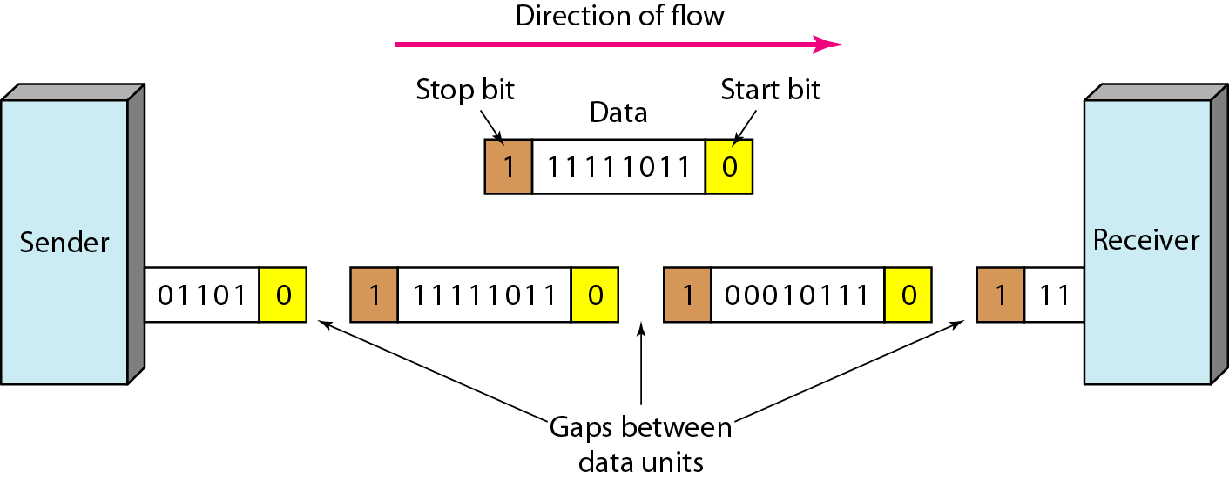
数据可以字节为单位,在任何时候抵达,双方都不需要时钟

因此需要在字节两头加上起始和结束的标志位,用以同步

同步传输

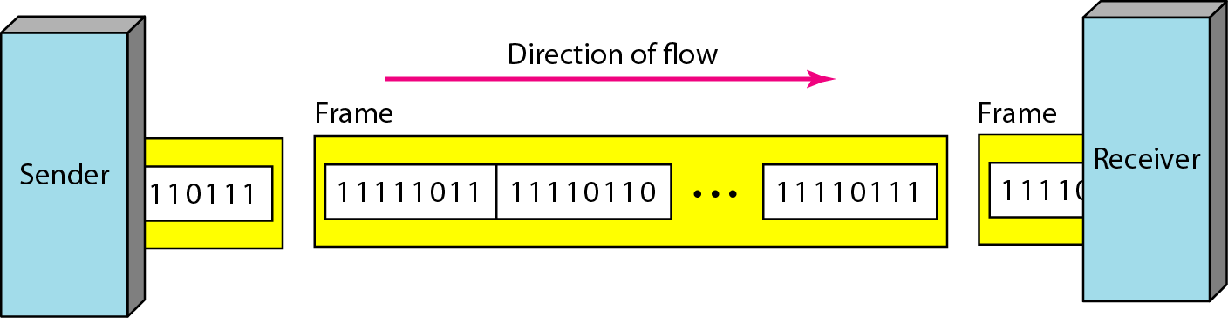
数据以帧为单位,双方需要有公共时钟,帧上没有起始结束标志,双方需要对拍

等时传输

数据以规定速率到达

比如实时音视频中,帧间的延迟应该相同且小,避免造成卡顿

模拟传输

概念区分

低通,带通,基带,宽带的关系:

基带通信使用低通信道

宽带通信使用带通信道

调频FM和频移键位FSK的关系?一个东西

数转模方法

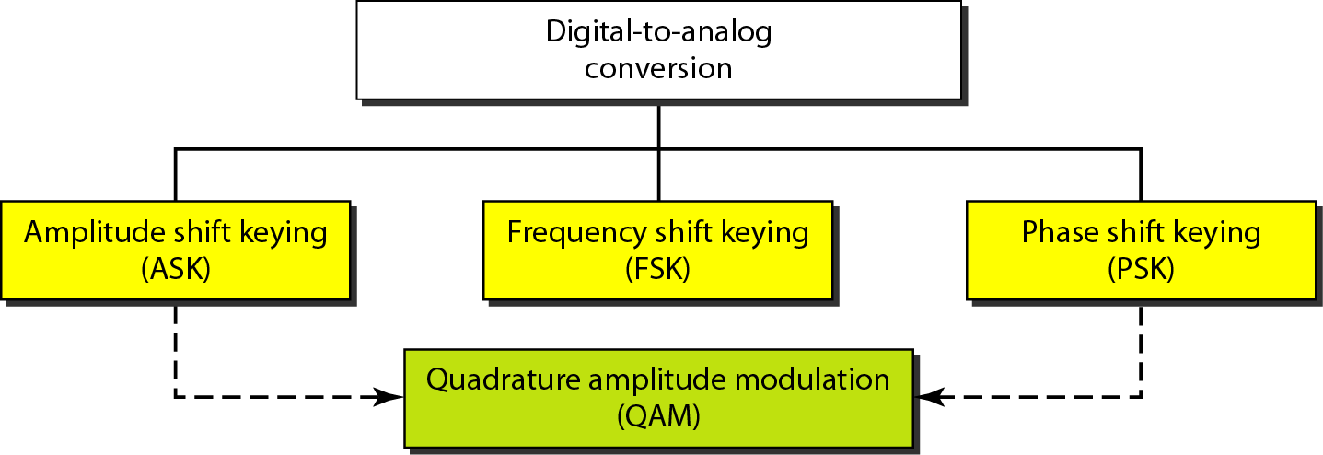
载波信号:发送设备产生高频信号作为基波承载信息

接收设备的收听频率和载波信号相同

数字信息通过改变载波信号的特性来将自身信息加到载波上去.称为调制或者移动键控

调制方法	调制图像	实现原理	带宽
二进制幅移键控BASK		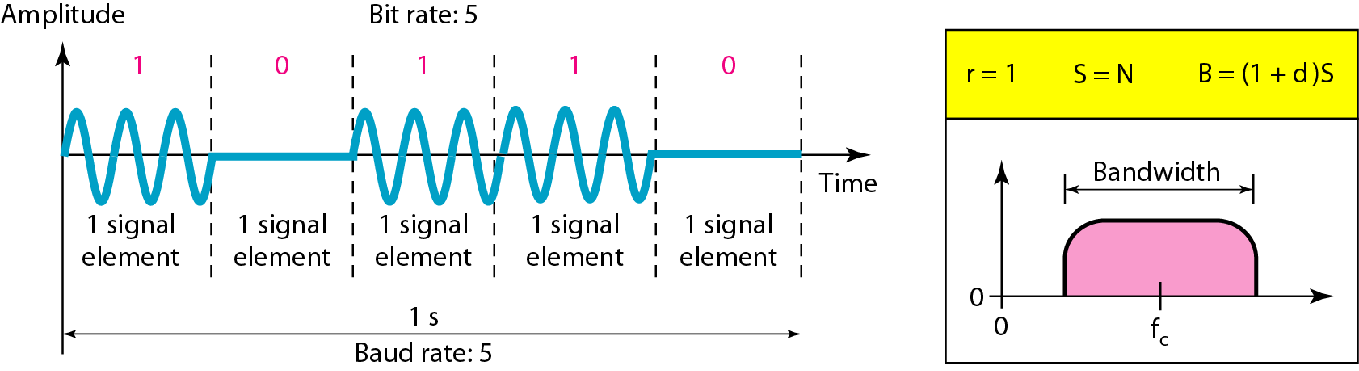	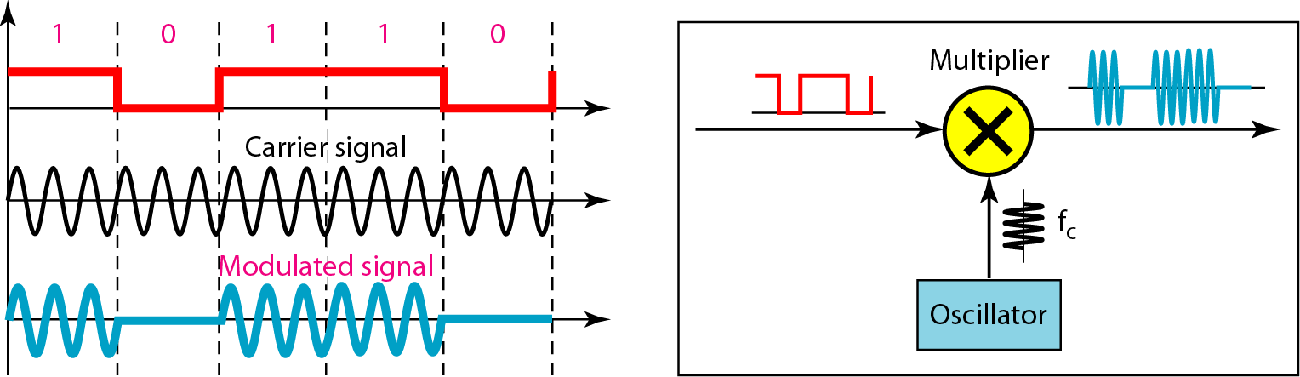$B=(1+d)\times S$
二进制频移键控BFSK		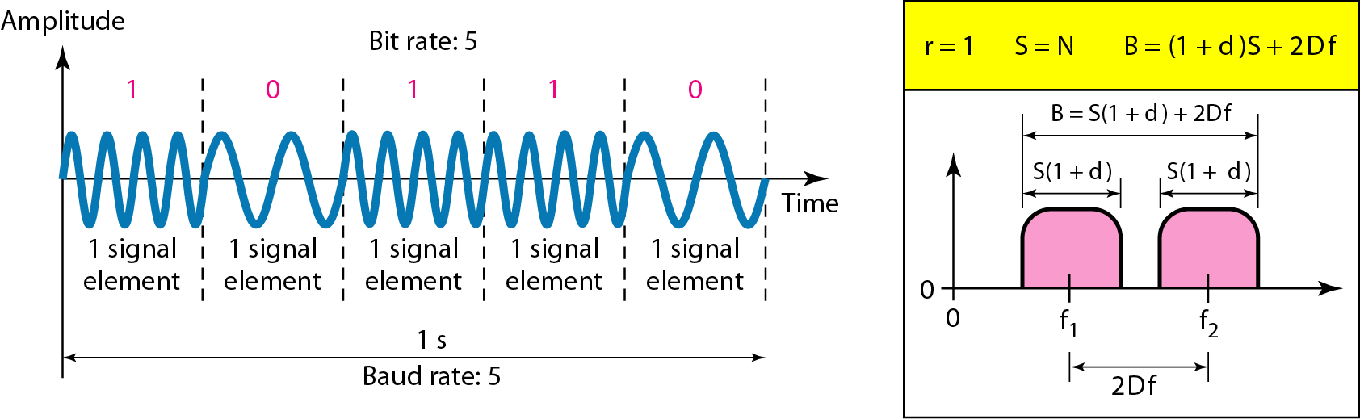	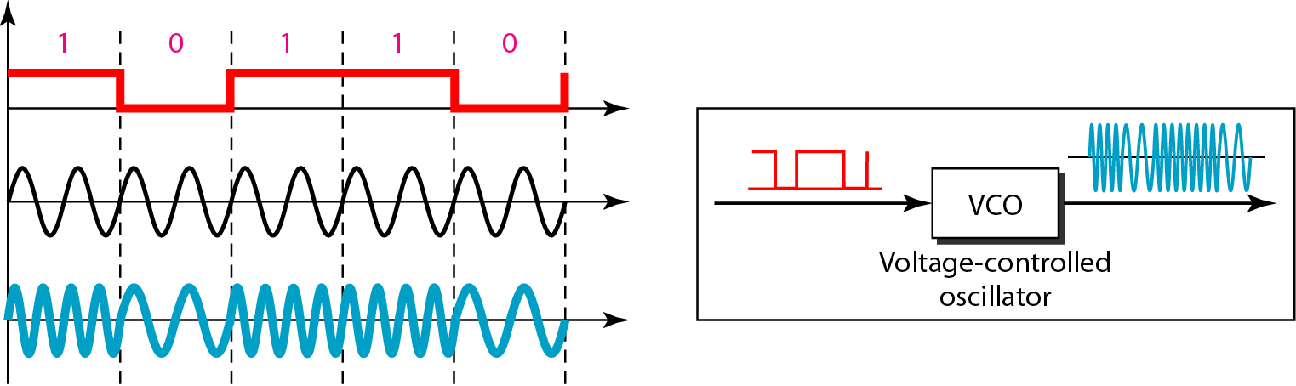$B=(1+d)\times S+2\Delta f$ 多电平时: $B = (1+d ) ×S + ( L -1 )2Δf $
二进制相移键控BPSK		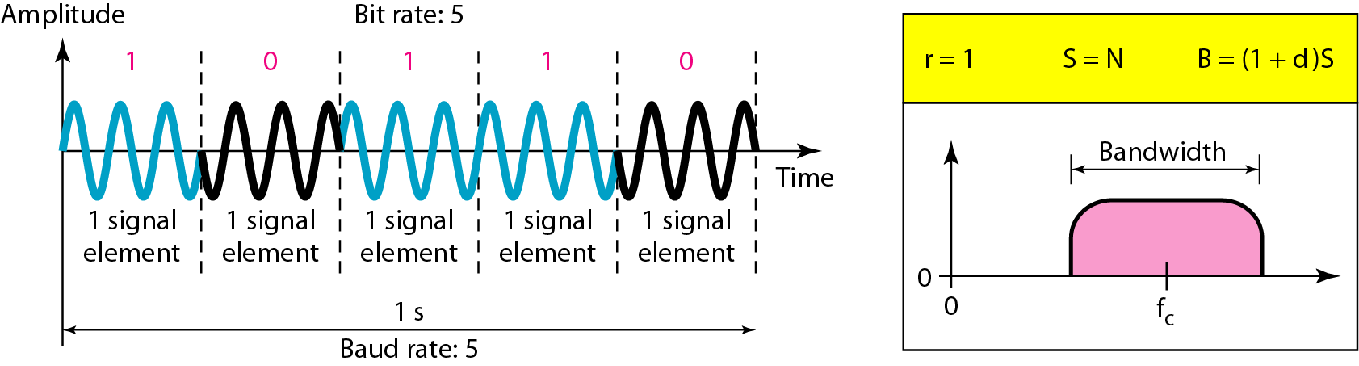	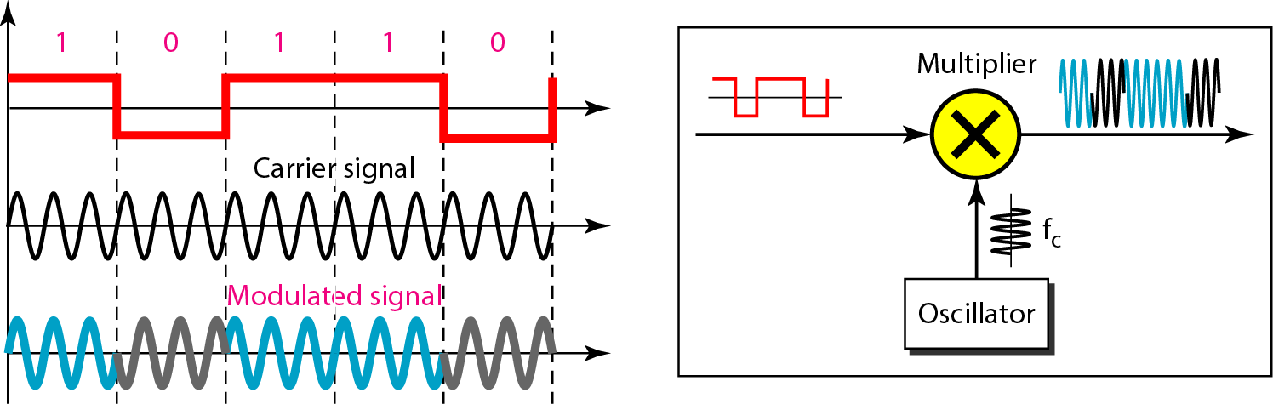$B=(1+d)\times S$
正交相移键控QPSK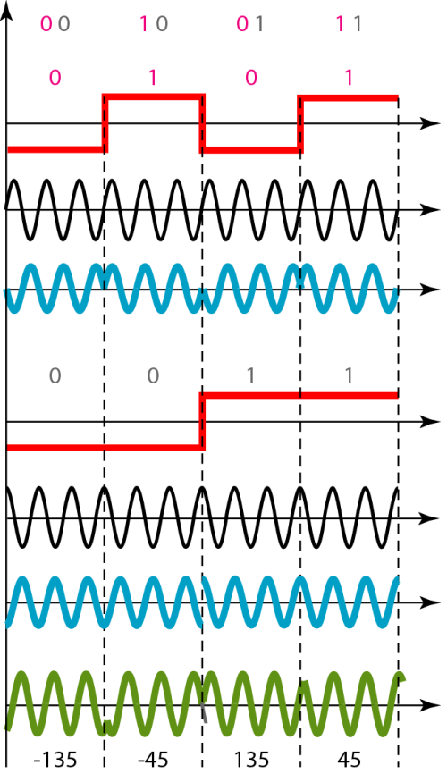

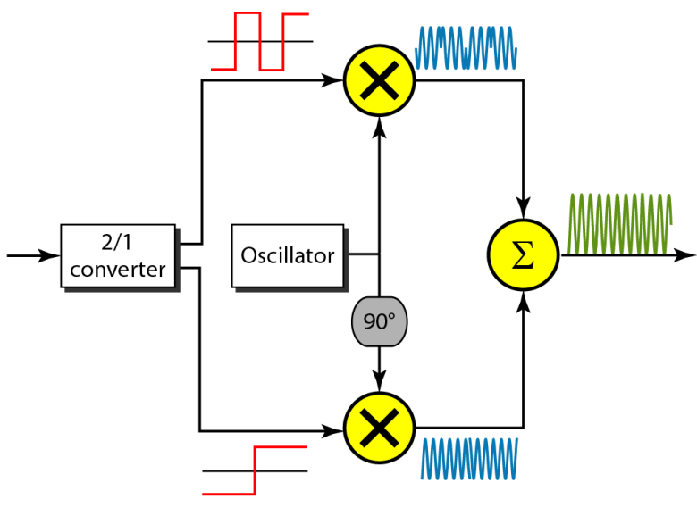这个正交相移键控是啥意思呢?

使用同一个信号,里面有两个大的正交分量载波信号

两个分量并行传送

假设要传输信号00'10'01'11

两个一组取前一个扔给一个载波分量

取后一个扔给另一个垂直的载波分量

不用两根导线就可以同时传输两路信息,这就是QPSK的目的

实际上就是两个BPSK的正交

模转模方法

模转模方法	图像及原理	带宽 B为原始模拟信号带宽
调幅AM		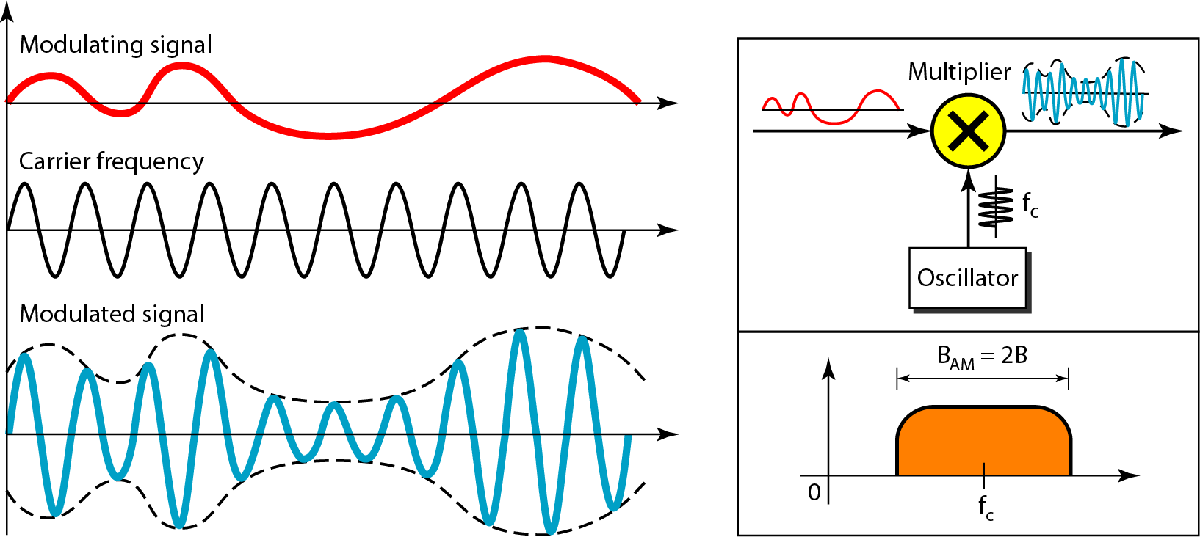$B_{AM} = 2B$
调频FM		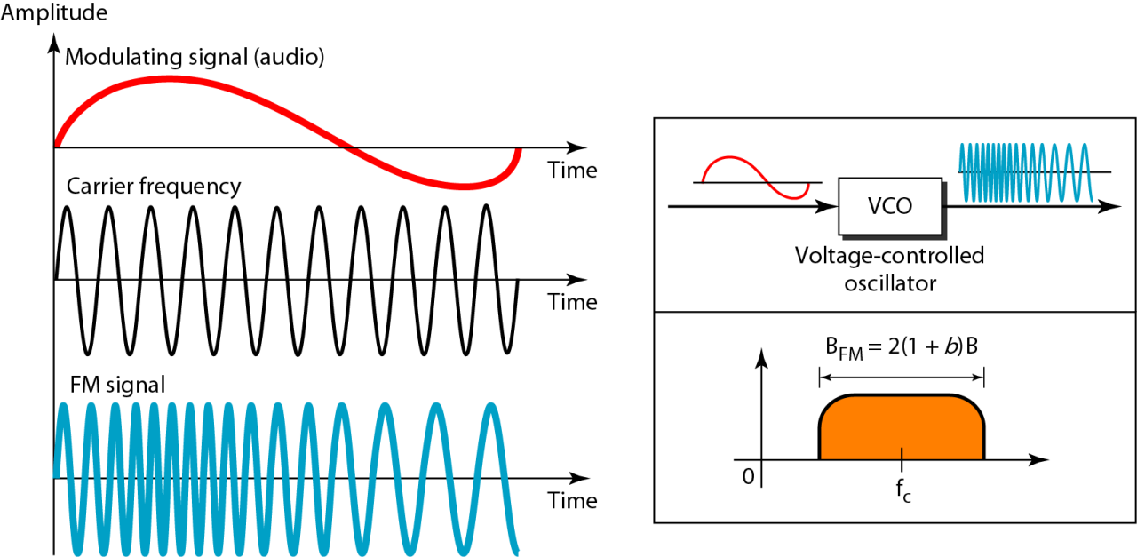$ B_{FM} = 2(1 + β)B$<br />其中$$为调制因子,通常设置为4
调相PM		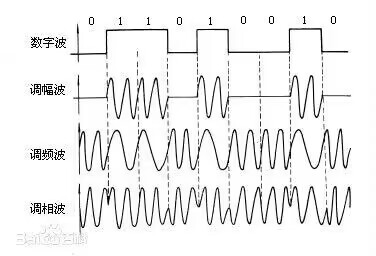$B_{PM} = 2(1 + β)B$

带宽利用

这部分没看懂

复用

复用技术	原理	备注
频分多路复用FDM		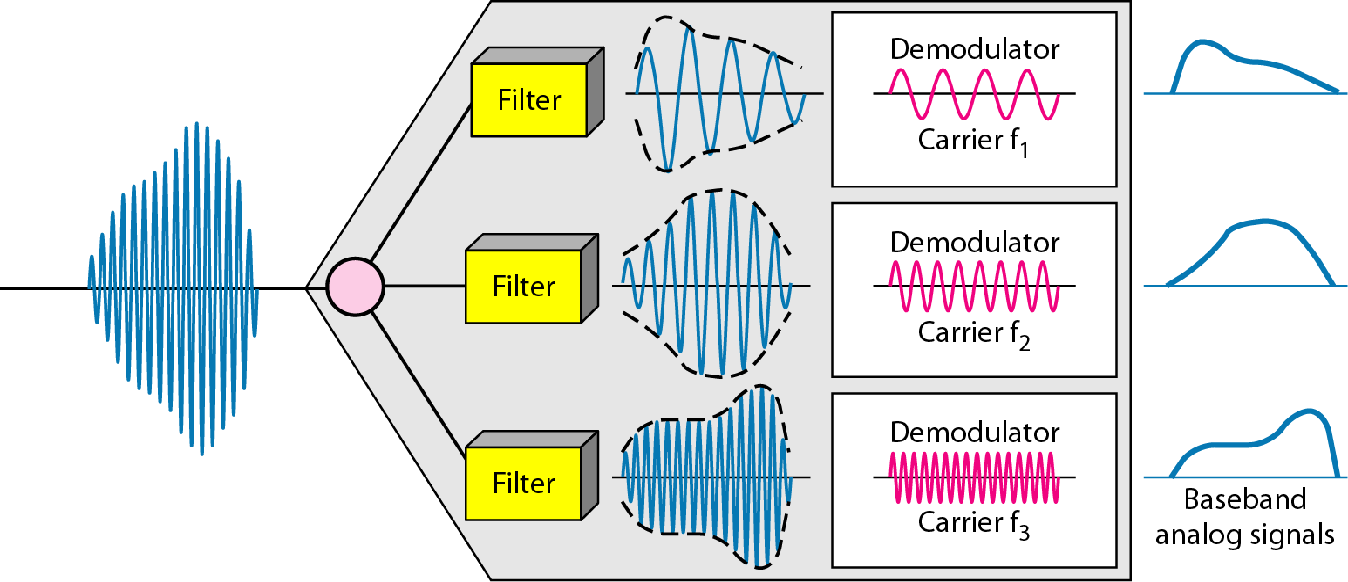合并模拟信号
波分多路复用WDM		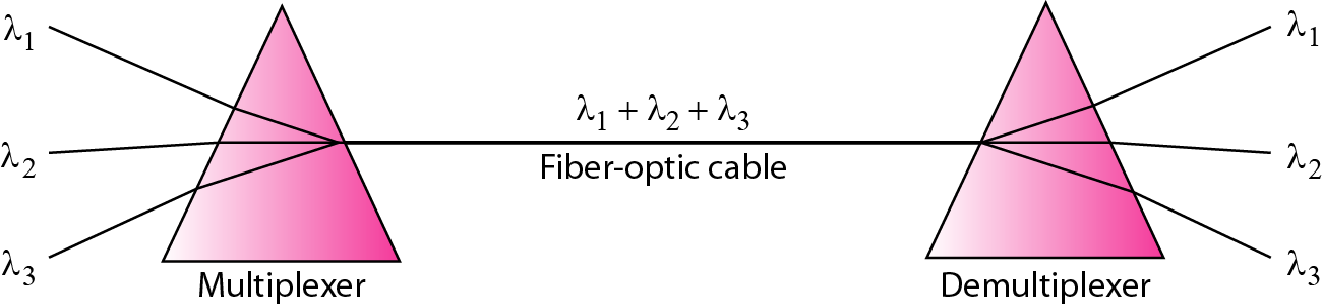合并光信号
时分多路复用TDM	同步时分复用和统计时分复用的区别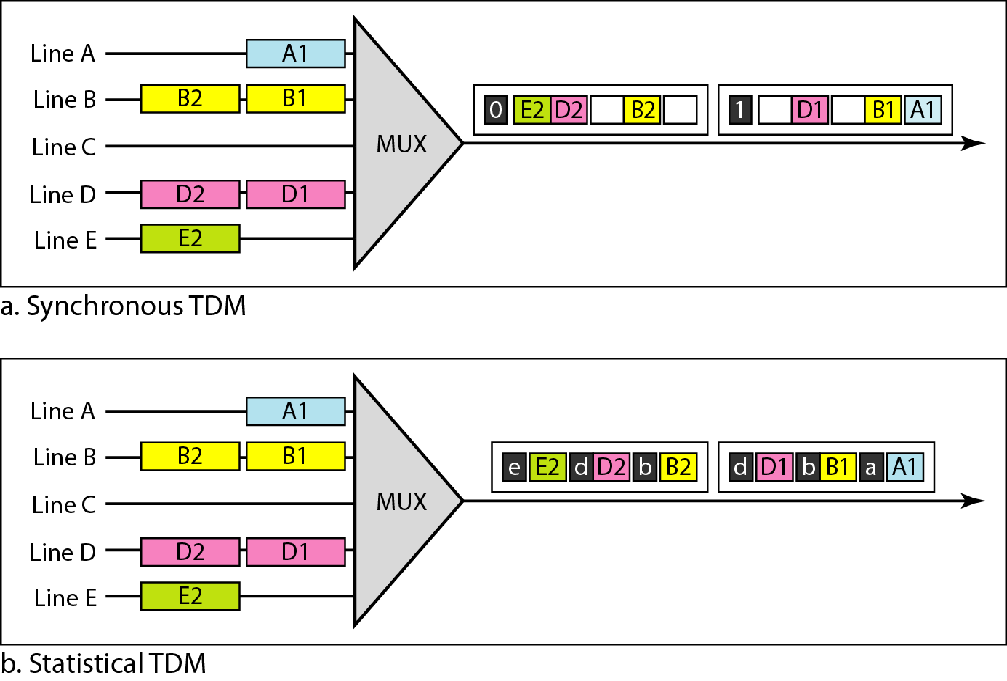	同步时分复用中,每一帧的最开始有一帧指示位用于同步,然后就是E,D,C,B,A每一路的数据,即使这一路上没有数据,也得用空时隙填充统计时分复用中是哪一路有数据才传输哪一路,在数据之前标注这是哪一路的数据

复用:允许使用一条数据链路传输多个信号的技术

扩频

麻了,啥玩意儿

调制方法	调制图像	实现原理	带宽
二进制幅移键控BASK			\(B=(1+d)\times S\)
二进制频移键控BFSK			\(B=(1+d)\times S+2\Delta f\) 多电平时: $B = (1+d ) ×S + ( L -1 )2Δf $
二进制相移键控BPSK			\(B=(1+d)\times S\)
正交相移键控QPSK

模转模方法	图像及原理	带宽 B为原始模拟信号带宽
调幅AM		\(B_{AM} = 2B\)
调频FM		$ B_{FM} = 2(1 + β)B\(<br />其中\)$为调制因子,通常设置为4
调相PM		\(B_{PM} = 2(1 + β)B\)